Dimensionality Reduction Dimensionality Reduction Highdimensional many features Find

Dimensionality Reduction

Dimensionality Reduction • High-dimensional == many features • Find concepts/topics/genres: – Documents: • Features: Thousands of words, millions of word pairs – Surveys – Netflix: 480 k users x 177 k movies Slides by Jure Leskovec 2

Dimensionality Reduction • Compress / reduce dimensionality: – 106 rows; 103 columns; no updates – random access to any cell(s); small error: OK Slides by Jure Leskovec 3

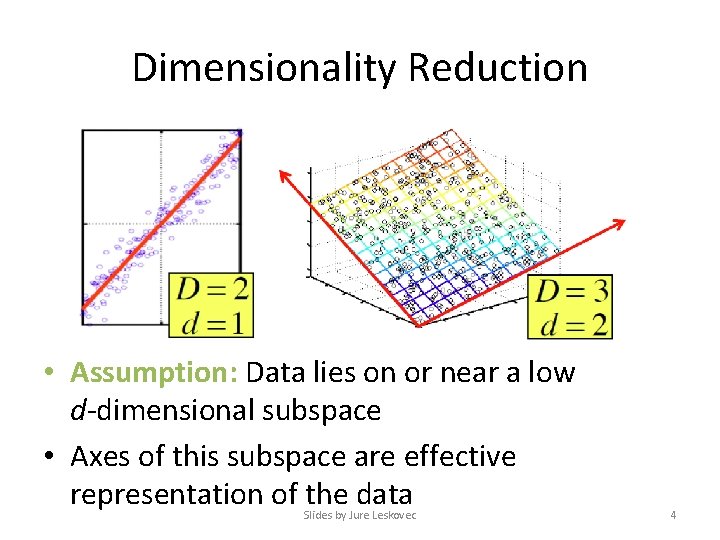
Dimensionality Reduction • Assumption: Data lies on or near a low d-dimensional subspace • Axes of this subspace are effective representation of the data Slides by Jure Leskovec 4

Why Reduce Dimensions? Why reduce dimensions? • Discover hidden correlations/topics – Words that occur commonly together • Remove redundant and noisy features – Not all words are useful • Interpretation and visualization • Easier storage and processing of the data Slides by Jure Leskovec 5

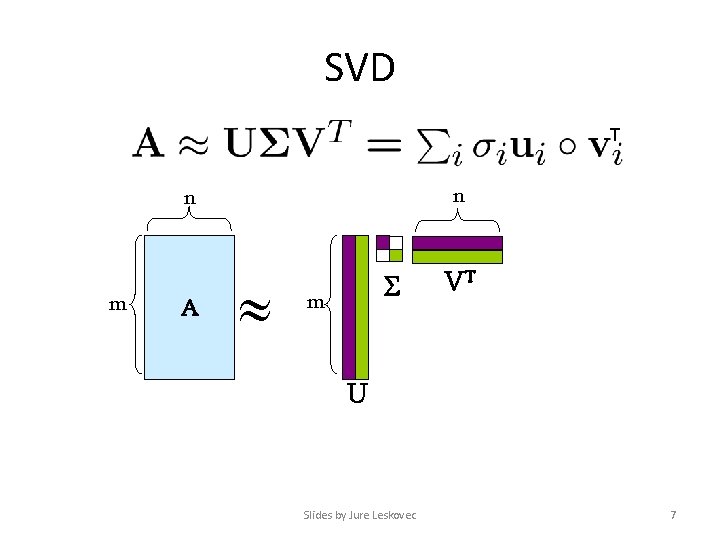
SVD - Definition A[m x n] = U[m x r] [ r x r] (V[n x r])T • A: Input data matrix – m x n matrix (e. g. , m documents, n terms) • U: Left singular vectors – m x r matrix (m documents, r concepts) • : Singular values – r x r diagonal matrix (strength of each ‘concept’) (r : rank of the matrix A) • V: Right singular vectors – n x r matrix (n terms, r concepts) Slides by Jure Leskovec 6

SVD T n n m A m VT U Slides by Jure Leskovec 7

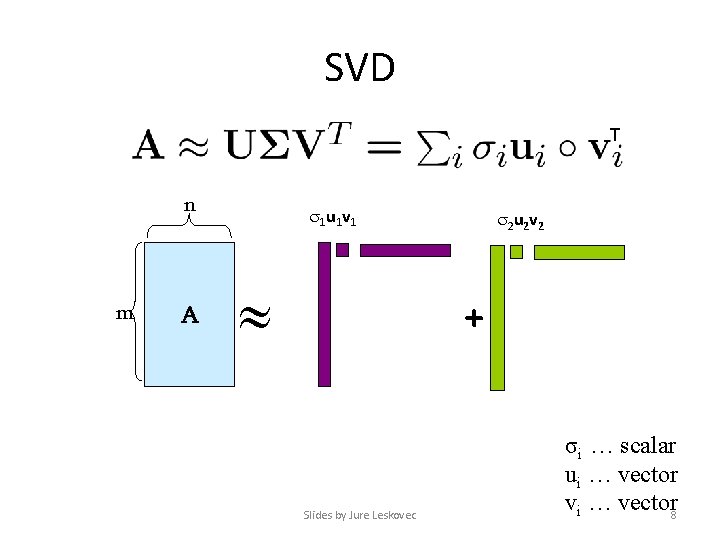
SVD T n m A 1 u 1 v 1 2 u 2 v 2 + Slides by Jure Leskovec σi … scalar ui … vector vi … vector 8

SVD - Properties It is always possible to decompose a real matrix A into A = U VT , where • U, , V: unique • U, V: column orthonormal: – UT U = I; VT V = I (I: identity matrix) – (Cols. are orthogonal unit vectors) • : diagonal – Entries (singular values) are positive, and sorted in decreasing order (σ1 σ2 . . . 0) Slides by Jure Leskovec 9

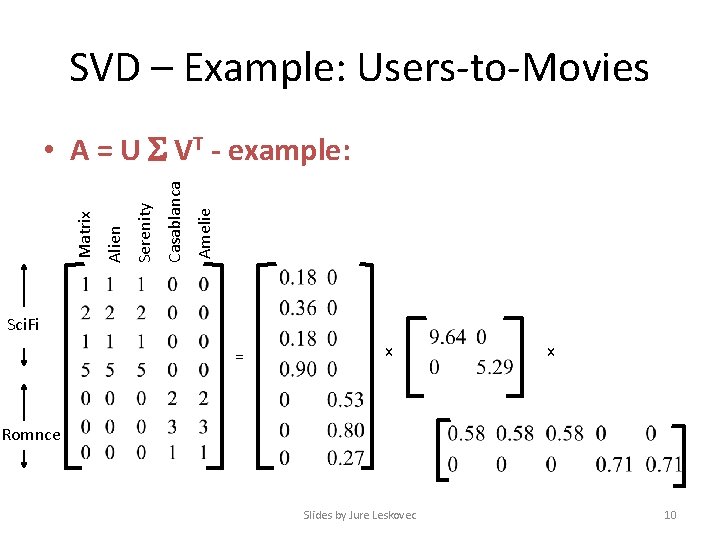
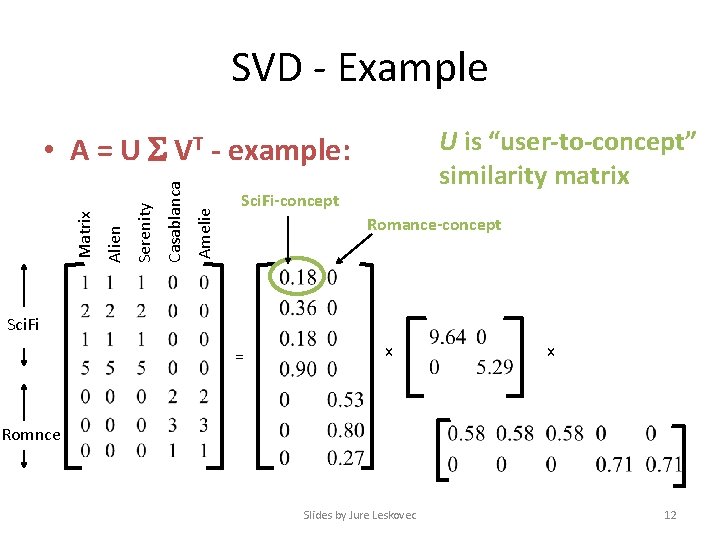
SVD – Example: Users-to-Movies Amelie Casablanca Serenity Alien Matrix • A = U VT - example: Sci. Fi = x x Romnce Slides by Jure Leskovec 10

SVD – Example: Users-to-Movies Amelie Casablanca Serenity Alien Matrix • A = U VT - example: Sci. Fi-concept Romance-concept Sci. Fi = x x Romnce Slides by Jure Leskovec 11

SVD - Example U is “user-to-concept” similarity matrix Amelie Casablanca Serenity Alien Matrix • A = U VT - example: Sci. Fi-concept Romance-concept Sci. Fi = x x Romnce Slides by Jure Leskovec 12

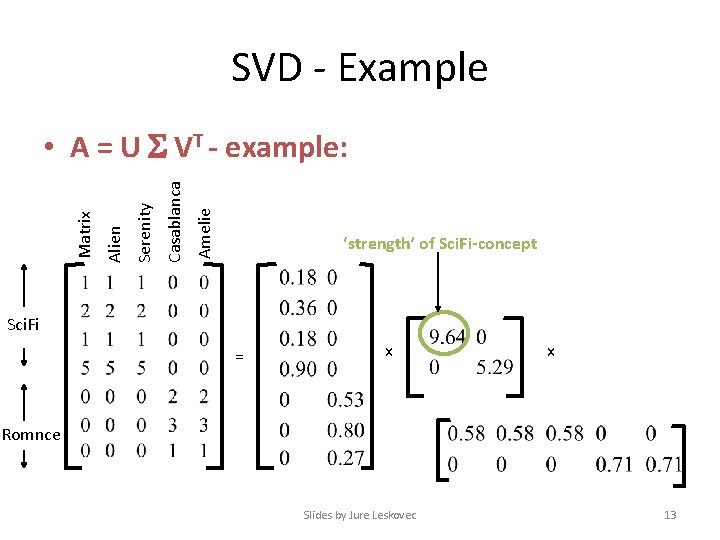
SVD - Example Amelie Casablanca Serenity Alien Matrix • A = U VT - example: ‘strength’ of Sci. Fi-concept Sci. Fi = x x Romnce Slides by Jure Leskovec 13

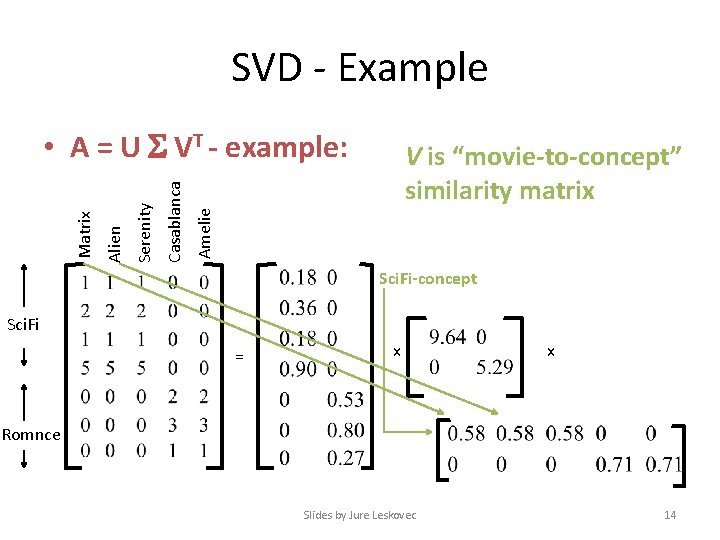
SVD - Example V is “movie-to-concept” similarity matrix Amelie Casablanca Serenity Alien Matrix • A = U VT - example: Sci. Fi-concept Sci. Fi = x x Romnce Slides by Jure Leskovec 14

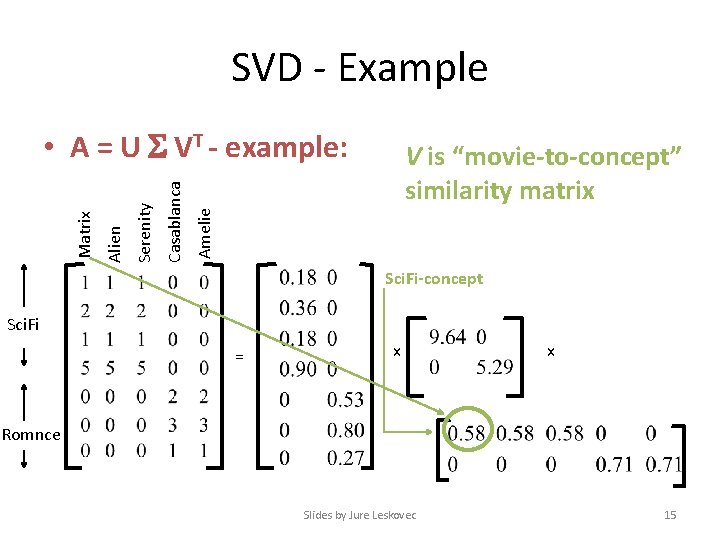
SVD - Example V is “movie-to-concept” similarity matrix Amelie Casablanca Serenity Alien Matrix • A = U VT - example: Sci. Fi-concept Sci. Fi = x x Romnce Slides by Jure Leskovec 15

SVD - Interpretation #1 ‘movies’, ‘users’ and ‘concepts’: • U: user-to-concept similarity matrix • V: movie-to-concept sim. matrix • : its diagonal elements: ‘strength’ of each concept Slides by Jure Leskovec 16

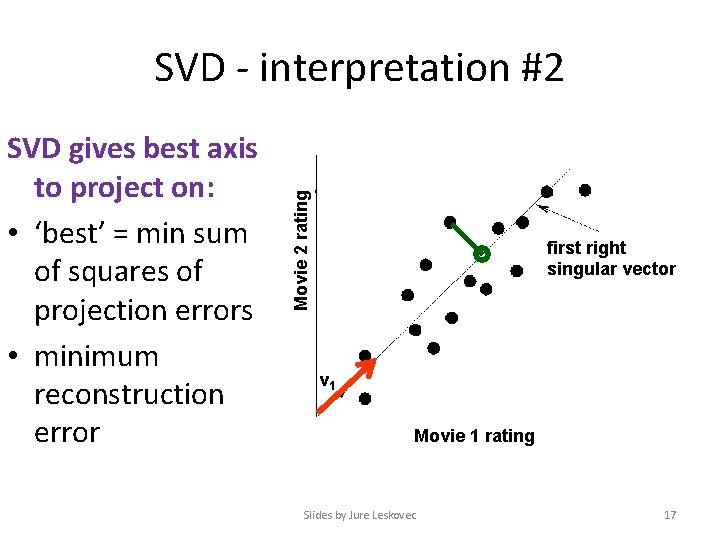
SVD gives best axis to project on: • ‘best’ = min sum of squares of projection errors • minimum reconstruction error Movie 2 rating SVD - interpretation #2 first right singular vector v 1 Movie 1 rating Slides by Jure Leskovec 17

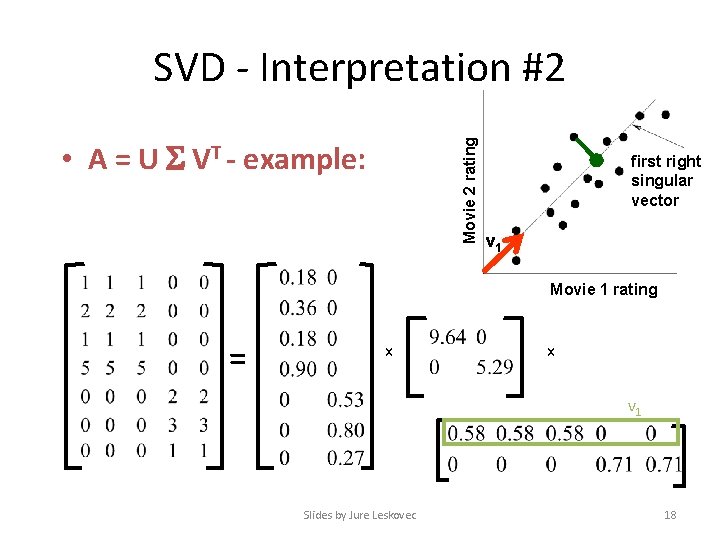
SVD - Interpretation #2 Movie 2 rating • A = U VT - example: first right singular vector v 1 Movie 1 rating = x x v 1 Slides by Jure Leskovec 18

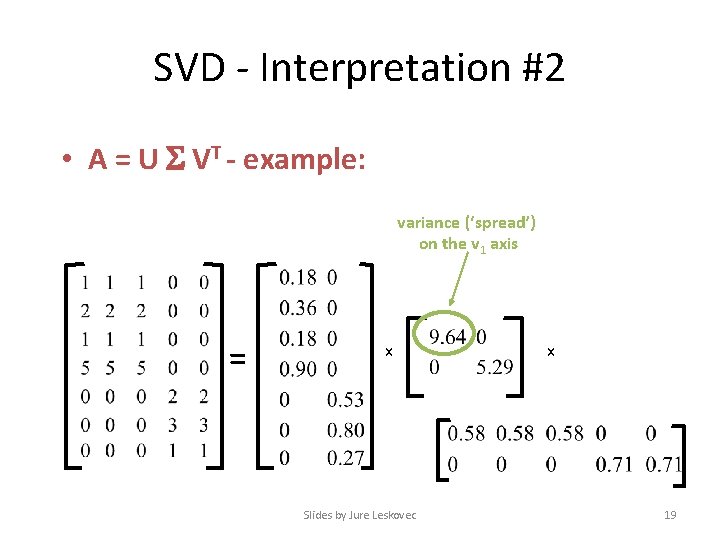
SVD - Interpretation #2 • A = U VT - example: variance (‘spread’) on the v 1 axis = x Slides by Jure Leskovec x 19

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? = x Slides by Jure Leskovec x 20

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? • A: Set the smallest singular values to zero = x x A= Slides by Jure Leskovec 21

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? • A: Set the smallest singular values to zero ~ x x A= Slides by Jure Leskovec 22

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? • A: Set the smallest singular values to zero: ~ x x A= Slides by Jure Leskovec 23

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? • A: Set the smallest singular values to zero: ~ x x A= Slides by Jure Leskovec 24

SVD - Interpretation #2 More details • Q: How exactly is dim. reduction done? • A: Set the smallest singular values to zero B= Frobenius norm: A= ǁMǁF = Σij Mij 2 ~ ǁA-BǁF = Σij (Aij-Bij)2 is “small” Slides by Jure Leskovec 25

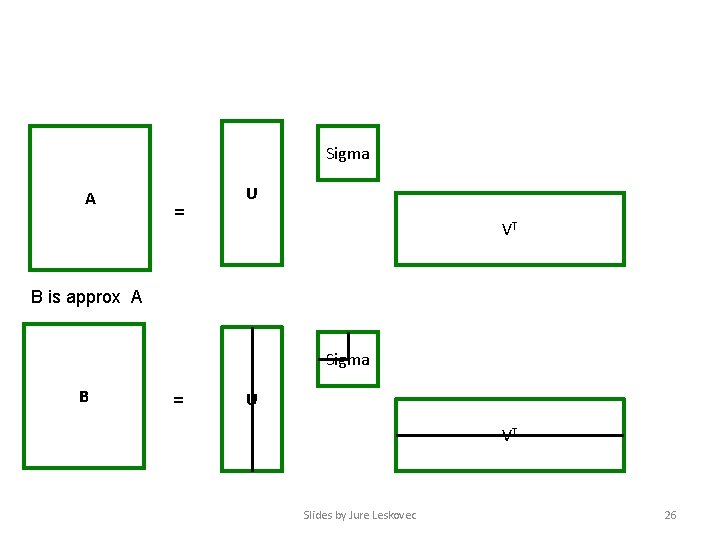
Sigma A = U VT B is approx A Sigma B = U VT Slides by Jure Leskovec 26

SVD – Best Low Rank Approx. • Slides by Jure Leskovec 27

SVD – Best Low Rank Approx. • We apply: -- P column orthonormal -- R row orthonormal -- Q is diagonal Slides by Jure Leskovec 28

SVD – Best Low Rank Approx. • U VT - U S VT = U ( - S) VT Slides by Jure Leskovec 29

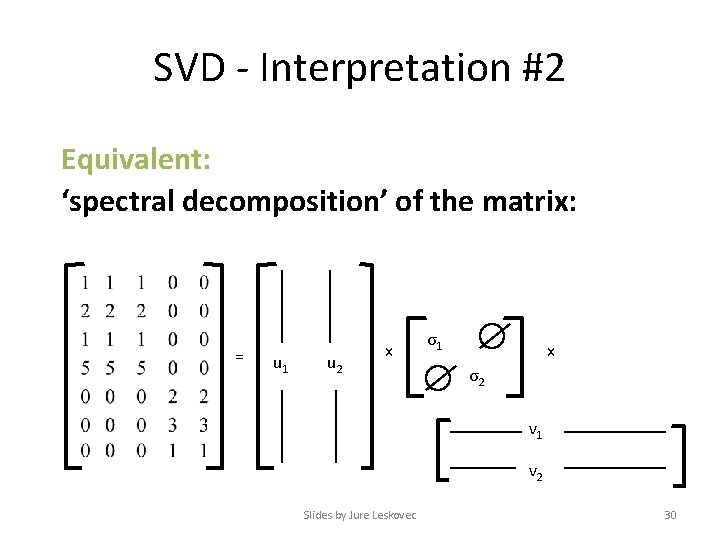
SVD - Interpretation #2 Equivalent: ‘spectral decomposition’ of the matrix: = u 1 u 2 x σ1 x σ2 v 1 v 2 Slides by Jure Leskovec 30

SVD - Interpretation #2 Equivalent: ‘spectral decomposition’ of the matrix m k terms = n u 1 σ1 nx 1 v. T 1 + σ2 u 2 v. T 2 +. . . 1 xm Assume: σ1 σ2 σ3 . . . 0 Why is setting small σs the thing to do? Vectors ui and vi are unit length, so σi scales them. So, zeroing small σs introduces less error. Slides by Jure Leskovec 31

SVD - Interpretation #2 Q: How many σs to keep? A: Rule-of-a thumb: keep 80 -90% of ‘energy’ (= σi 2) m n = σ1 u 1 v. T 1 + σ2 u 2 v. T 2 +. . . assume: σ1 σ2 σ3 . . . Slides by Jure Leskovec 32

SVD - Complexity • To compute SVD: – O(nm 2) or O(n 2 m) (whichever is less) • But: – Less work, if we just want singular values – or if we want first k singular vectors – or if the matrix is sparse • Implemented in linear algebra packages like – LINPACK, Matlab, SPlus, Mathematica. . . Slides by Jure Leskovec 33

SVD - Conclusions so far • SVD: A= U VT: unique – U: user-to-concept similarities – V: movie-to-concept similarities – : strength of each concept • Dimensionality reduction: – keep the few largest singular values (80 -90% of ‘energy’) – SVD: picks up linear correlations Slides by Jure Leskovec 34

Case study: How to query? Amelie Casablanca Serenity Alien Matrix Q: Find users that like ‘Matrix’ and ‘Alien’ Sci. Fi = x x Romnce Slides by Jure Leskovec 35

Case study: How to query? Amelie Casablanca Serenity Alien Matrix Q: Find users that like ‘Matrix’ A: Map query into a ‘concept space’ – how? Sci. Fi = x x Romnce Slides by Jure Leskovec 36

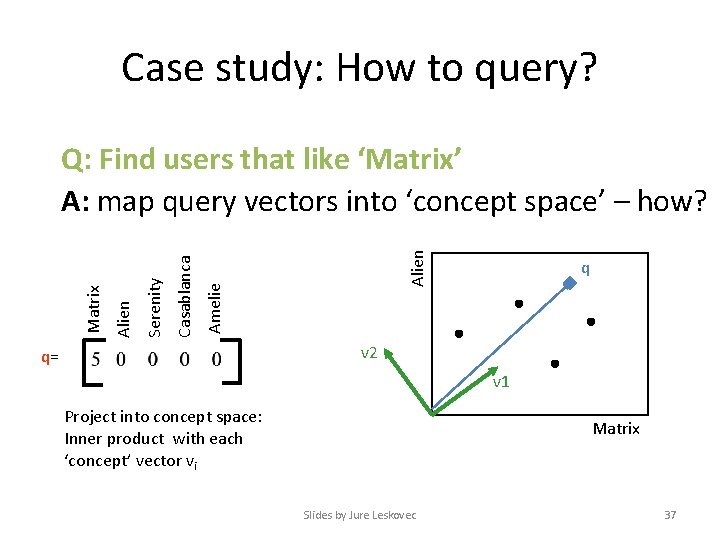
Case study: How to query? Alien Amelie Casablanca Serenity Alien Matrix Q: Find users that like ‘Matrix’ A: map query vectors into ‘concept space’ – how? q v 2 q= v 1 Project into concept space: Inner product with each ‘concept’ vector vi Matrix Slides by Jure Leskovec 37

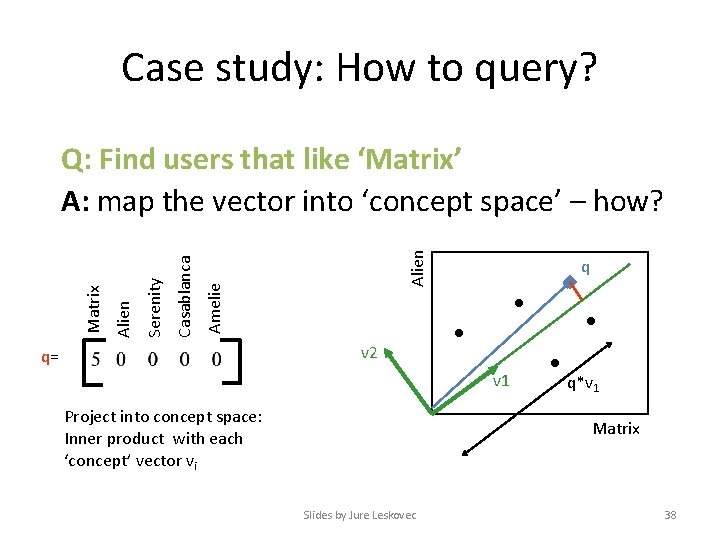
Case study: How to query? Alien Amelie Casablanca Serenity Alien Matrix Q: Find users that like ‘Matrix’ A: map the vector into ‘concept space’ – how? q v 2 q= v 1 Project into concept space: Inner product with each ‘concept’ vector vi q*v 1 Matrix Slides by Jure Leskovec 38

Case study: How to query? Sci. Fi-concept Amelie Casablanca Alien Matrix E. g. : Serenity Compactly, we have: qconcept = q V = q= movie-to-concept similarities Slides by Jure Leskovec 39

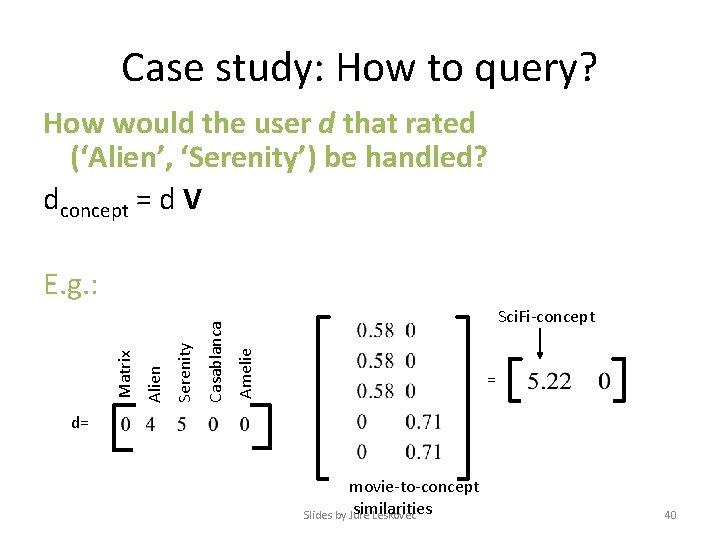
Case study: How to query? How would the user d that rated (‘Alien’, ‘Serenity’) be handled? dconcept = d V Sci. Fi-concept Amelie Casablanca Serenity Alien Matrix E. g. : = d= movie-to-concept similarities Slides by Jure Leskovec 40

Case study: How to query? Amelie Casablanca Serenity Alien Matrix Observation: User d that rated (‘Alien’, ‘Serenity’) will be similar to query “user” q that rated (‘Matrix’), although d did not rate ‘Matrix’! Sci. Fi-concept d= q= Similarity = 0 Similarity ≠ 0 Slides by Jure Leskovec 41

SVD: Drawbacks + Optimal low-rank approximation: • in Frobenius norm - Interpretability problem: – A singular vector specifies a linear combination of all input columns or rows - Lack of sparsity: – Singular vectors are dense! VT = U Slides by Jure Leskovec 42