The Function Concept DEFINITION A function consists of





























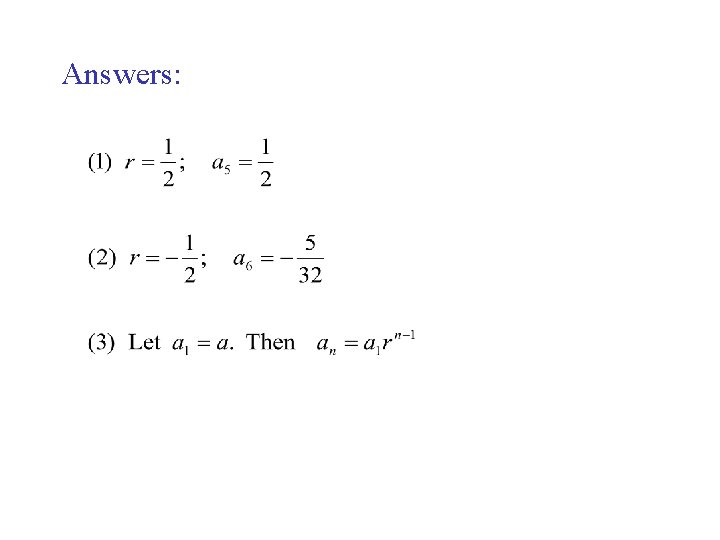







- Slides: 46

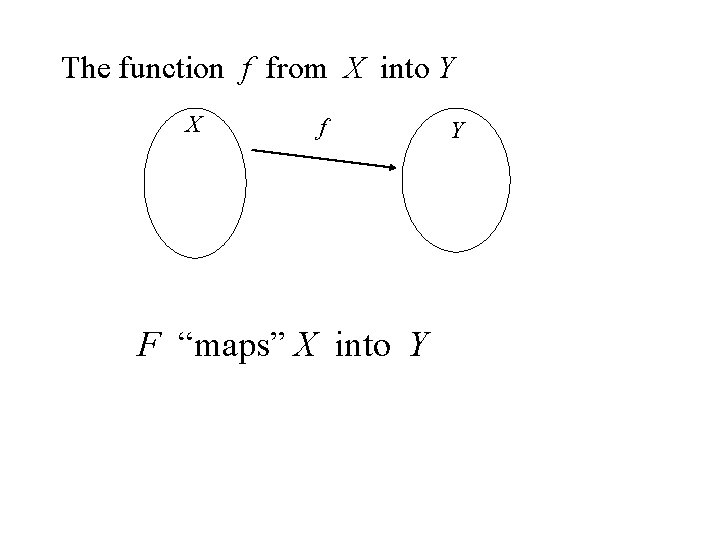
The Function Concept • DEFINITION: A function consists of two nonempty sets X and Y and a rule f that associates each element x in X with one and only one element y in Y. Read “The function f from X into Y” and symbolized by f : X Y.

The function f from X into Y X f F “maps” X into Y Y

Some examples: • Supermarket item price • Student chair • College student GPA • Worker SSN • Car license plate “number” • Real number x x 2

More examples: Are these functions? ? ? X Y • Dormitory rooms Students Rule: room student(s) assigned • Airplane luggage Passengers Rule: piece(s) of luggage passenger • Nine digit numbers Workers Rule: number worker’s SSN • Real numbers Rule: x the numbers y such that y 2= x

Another defintion: Let X and Y be sets. A function f from X into Y is a set S of ordered pairs (x, y), x X, y Y, with the property that (x 1, y 1) and (x 1, y 2) are in S if and only if y 1 = y 2.

Examples

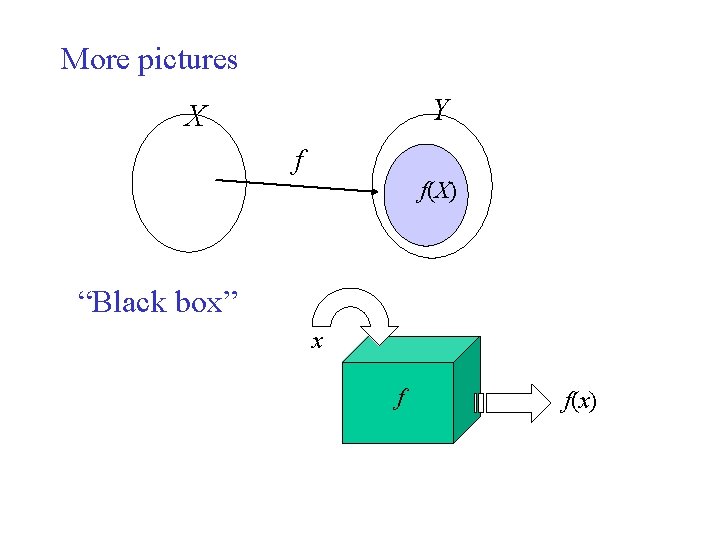
Some Terminology & Notation Let f : X Y. The set X (the “first” set) is called the domain of the function. The set of y’s in Y which correspond to an element x in X is called the range of the function. The range of f is, in general a subset of Y.

Variables: Let f : X Y. The symbols x and y are called variables. In particular, a symbol such as x, representing an arbitrary element in the domain is called an independent variable. A symbol such as y, representing an element in the range corresponding to an element x in the domain is called a dependent variable.

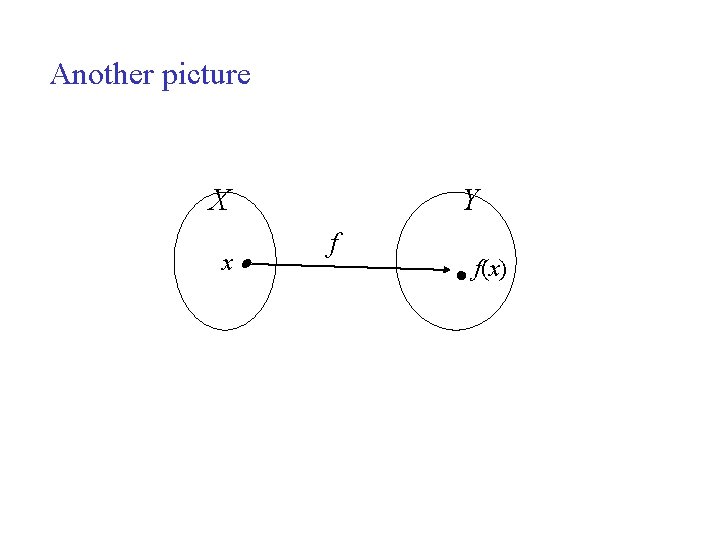
Function notation: Let f : X Y. Pick an element x in X and apply the rule f. This produces a unique element in Y. The symbol f(x) is used to denote that element. f(x) is read “f of x” or “the value of f at x” or “the image of x under f.

Another picture X x Y f f(x)

More pictures Y X f f(X) “Black box” x f f(x)

One-to-one functions: Let f : X Y. f is a one-to-one function if it takes distinct elements in the domain to distinct elements in the range. That is: f is one-to-one if x 1 x 2 implies Notation: f is 1 – 1. f(x 1) f(x 2).

Examples: Which of these function is 1 – 1? • Supermarket item price • Student GPA • Car license plate “number” • f(x) = 2 x + 3

Inverse functions Suppose f : X Y is 1 – 1. Then there is a function g: f(X) X such that g(f(x)) = x for all x X. X f Y f(X) g g is called the inverse of f and is denoted by f -1

Functions in Mathematics • From Geometry and Measurement: 1. Length function: x is a line segment, l(x) = the length of x. 2. Area functions: x is a rectangle, A(x) = the area of x. 3. Volume functions: x is a sphere, V(x) = the volume of x. • From Probability & Statistics: E is a subset (event) in a sample space S, P(E) = the probability that E “occurs”.

Functions in “Algebra” Let f : X Y where X is a given set of real numbers and Y is the set of all real numbers. “f is a real-valued function of a real variable” Note: The domain X may or may not be the set of all real numbers. Examples:

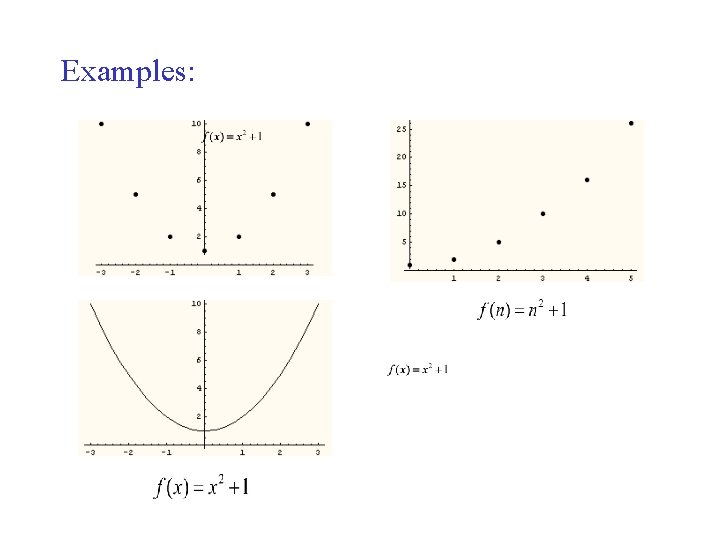
Graph of a function Let f : X Y. The graph of f is the set of points (x, f(x)) plotted in the coordinate plane: Graph of f = {(x, f(x)) | x X }. The graph of f is a “geometric” object – a “picture” of the function.

Examples:

Functions defined on the positive integers: Sequences A function f whose domain is the set of positive integers is called a sequence. The values are called the terms of the sequence; f(1) is the 1 st term, f(2) is the 2 nd term, and so on

Subscript notation It is customary to use subscript notation rather than functional notation: and to denote the sequence by an

Examples

Recursion formulas A recursion formula or recurrence relation gives ak+1 in terms of one or more of the terms am that precede ak+1. Examples: Find the first four terms and the nth term for the sequence specified by

Solutions

More examples (3) List the first six terms of the sequence whose nth term an is the nth prime number. Give a “formula” for an. (4) The first four terms of the sequence an are: What is the 5 th term?

Answers (1) 2, 3, 5, 7, 11, 13; an = ? ? ? (2)

Limits of sequences Given a sequence an. What is the behavior of an for very large n ? That is, as n what can you say about an ? Examples:

Answers (1) 1 (2) 0 (3) No limit (4) No limit

Two special sequences 1. Arithmetic sequences: A sequence is an arithmetic sequence (arithmetic progression) if successive terms differ by a constant d, called the common difference. That is an arithmetic sequence if

Examples Answers: (1) Yes (2) No (3) Yes, assuming the pattern goes on as indicated

(4)What is the 12 th term of the arithmetic sequence whose first three terms are: 1, 5, 9?

Solving the recursion formula

Geometric sequences A geometric sequence is a sequence in which the ratio of successive terms is a nonzero constant r. That is, The number r is called the common ratio.

Examples (1)The sequence 8, 4, 2, 1, …. is a geometric sequence. Find the common ratio and give the 5 th term. (2) The sequence is a geometric sequence, find the common ratio and give the 6 th term. (3) an geometric sequence with common ratio r. Give a formula for an.
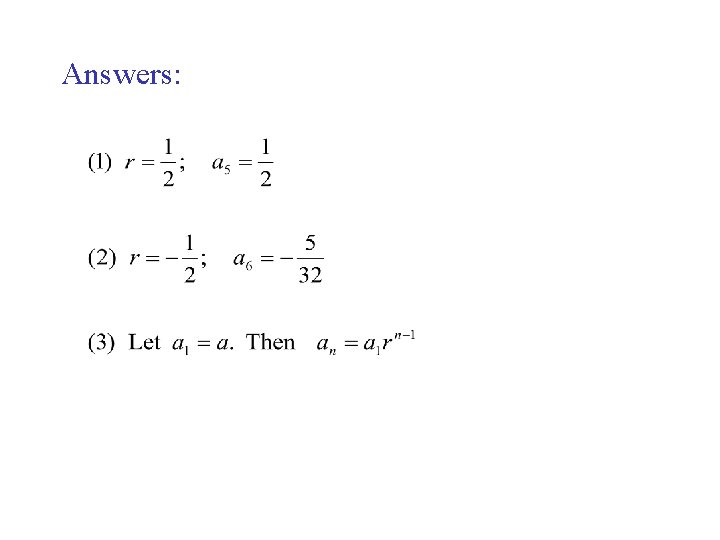
Answers:

Function defined on intervals Let f : X Y where X is an interval or a union of intervals and Y is the set of real numbers. The graph of f is the set of all points (x, f(x)) in the coordinate plane. The graph of f is the graph of the equation y=f (x).

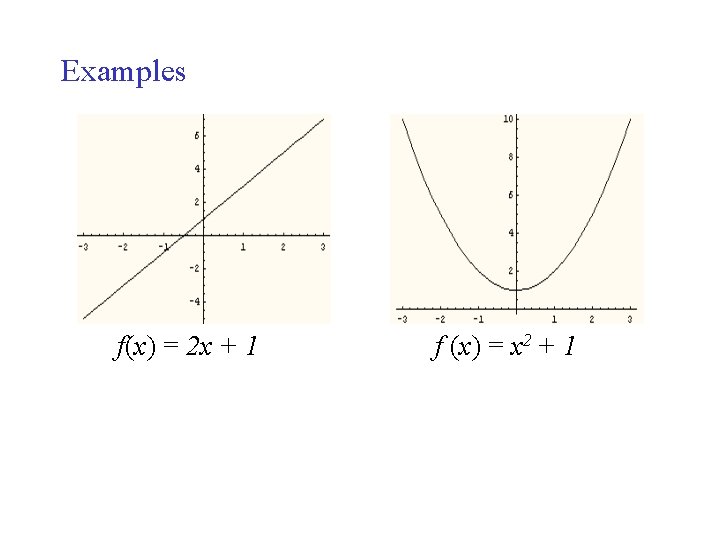
Examples f(x) = 2 x + 1 f (x) = x 2 + 1

The Elementary Functions 1. The constant functions: The graph of f is a horizontal line c units above or below the x-axis depending on the sign of c. f (x) = 2

(2) The identity function and linear functions (a) The function f (x) = x is called the identity function. The graph is


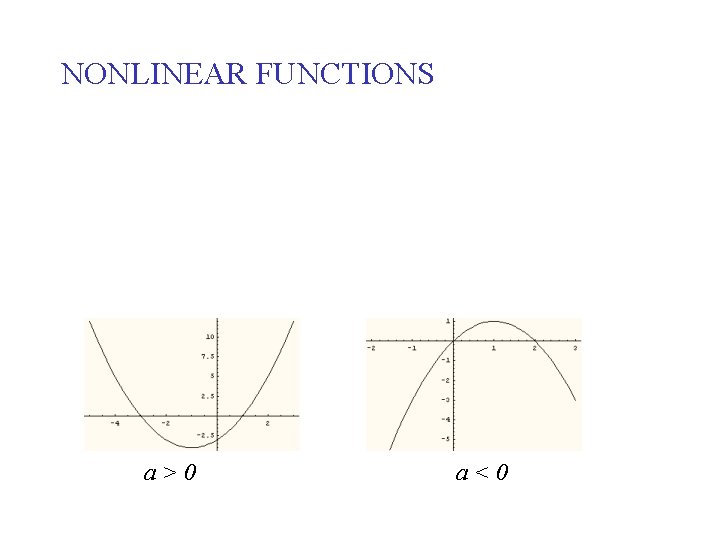
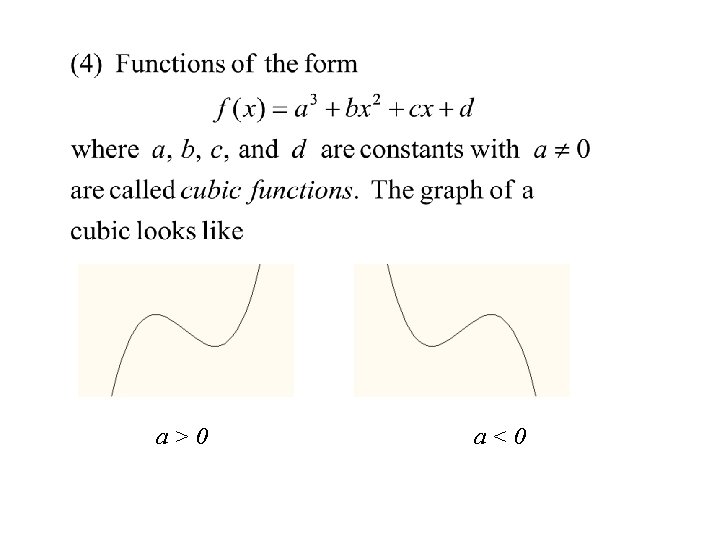
NONLINEAR FUNCTIONS a>0 a<0

a>0 a<0

(5) Polynomial Functions


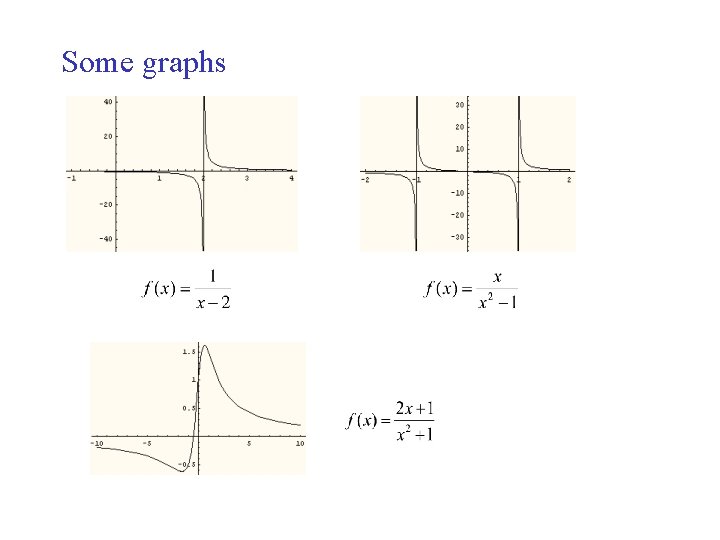
(6) Rational functions

Some graphs

The Elementary Functions (7) Algebraic functions: sums, differences, products, quotients and roots of rational functions. (8) The trigonometric functions. (9) Exponential functions. (10) Logarithm functions.
 What is a function
What is a function Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Chụp tư thế worms-breton
Chụp tư thế worms-breton Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia Các môn thể thao bắt đầu bằng tiếng đua
Các môn thể thao bắt đầu bằng tiếng đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Cong thức tính động năng
Cong thức tính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng xinh xinh thế chỉ nói điều hay thôi
Cái miệng xinh xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Thứ tự các dấu thăng giáng ở hóa biểu
Thứ tự các dấu thăng giáng ở hóa biểu Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Fecboak
Fecboak Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Số nguyên là gì
Số nguyên là gì Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Hổ đẻ mỗi lứa mấy con
Hổ đẻ mỗi lứa mấy con Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Hệ hô hấp
Hệ hô hấp Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Real self examples list
Real self examples list Pengertian marketing concept
Pengertian marketing concept Function prototype and function definition
Function prototype and function definition Work energy theorem
Work energy theorem