QUADRATIC FUNCTIONS Monika V Sikand Light and Life

QUADRATIC FUNCTIONS Monika V Sikand Light and Life Laboratory Department of Physics and Engineering physics Stevens Institute of Technology Hoboken, New Jersey, 07030.

OUTLINE Graphing Quadratic Functions Solving Quadratic Equations by Factoring Solving Quadratic Equations by Finding Square Roots Complex Numbers The Quadratic Formula and the Discriminant Graphing and Solving Quadratic Inequalities Modeling with Quadratic Functions

Graphing Quadratic Functions

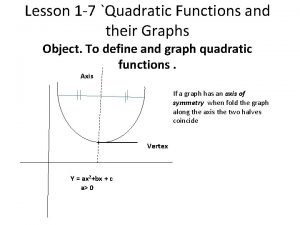
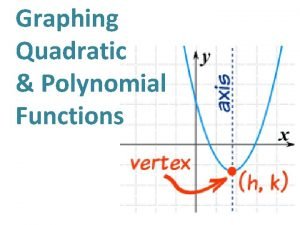
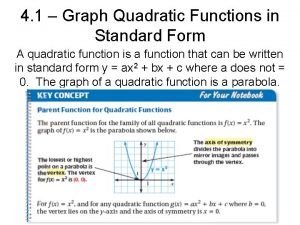
A QUADRATIC FUNCTION A quadratic function has a form y = ax 2 + bx + c where a ≠ 0. The graph of a quadratic function is Ushaped and is called parabola. The lowest or highest point on the graph of a quadratic function is called the vertex. The graphs of y = x 2 and y = -x 2 are symmetric about the y-axis, called the axis of symmetry. y = x 2 vertex y = -x 2 Axis of symmetry

THE GRAPH OF A QUADRATIC FUNCTION The parabola opens up if a>0 and opens down if a<0. The parabola is wider than the graph of y = x 2 if |a| < 1 and narrower than the graph of y = x 2 if |a| > 1. The x-coordinate of the vertex is -b/(2 a). The axis of symmetry is the vertical line x = -b/(2 a). y = x 2 vertex y = -x 2 Axis of symmetry

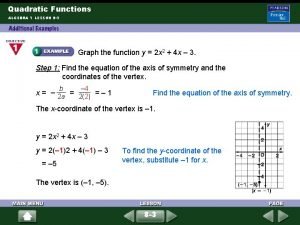
EXAMPLE Graph y = 2 x 2 -8 x +6 Solution: The coefficients for this function are a = 2, b = -8, c = 6. Since a>0, the parabola opens up. The x-coordinate is: x = -b/2 a, x = -(-8)/(2(2)) x = 2 The y-coordinate is: y = 2(2)2 -8(2)+6 y = -2 Hence, the vertex is (2, -2).

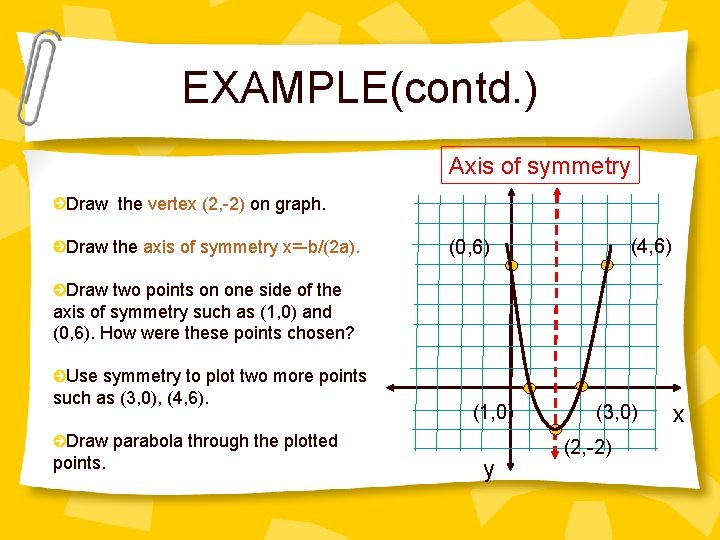
EXAMPLE(contd. ) Axis of symmetry Draw the vertex (2, -2) on graph. Draw the axis of symmetry x=-b/(2 a). (4, 6) (0, 6) Draw two points on one side of the axis of symmetry such as (1, 0) and (0, 6). How were these points chosen? Use symmetry to plot two more points such as (3, 0), (4, 6). Draw parabola through the plotted points. (1, 0) y (3, 0) (2, -2) x

VERTEX FORM OF QUADRATIC EQUATION y = a(x - h)2 + k The vertex is (h, k). The axis of symmetry is x = h.

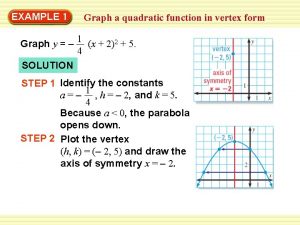
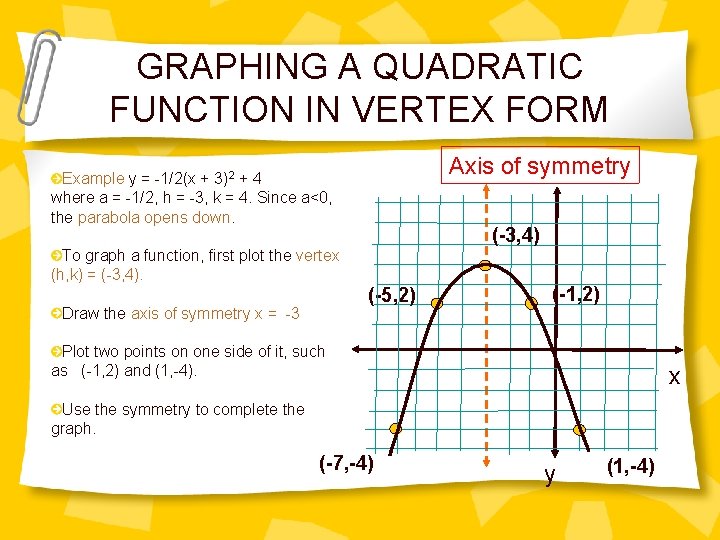
GRAPHING A QUADRATIC FUNCTION IN VERTEX FORM Axis of symmetry Example y = -1/2(x + 3)2 + 4 where a = -1/2, h = -3, k = 4. Since a<0, the parabola opens down. (-3, 4) To graph a function, first plot the vertex (h, k) = (-3, 4). (-5, 2) Draw the axis of symmetry x = -3 (-1, 2) Plot two points on one side of it, such as (-1, 2) and (1, -4). x Use the symmetry to complete the graph. (-7, -4) y (1, -4)

INTERCEPT FORM OF QUADRATIC EQUATION y = a(x - p)(x - q) The x intercepts are p and q. The axis of symmetry is halfway between (p, 0) and (q, 0).

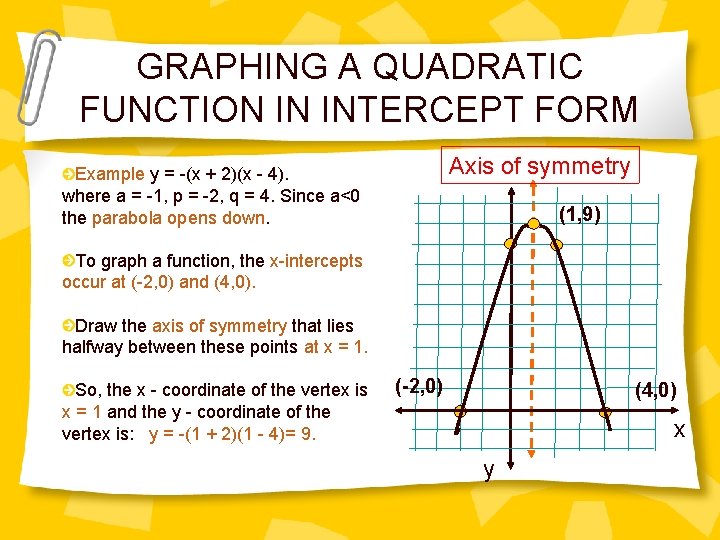
GRAPHING A QUADRATIC FUNCTION IN INTERCEPT FORM Example y = -(x + 2)(x - 4). where a = -1, p = -2, q = 4. Since a<0 the parabola opens down. Axis of symmetry (1, 9) To graph a function, the x-intercepts occur at (-2, 0) and (4, 0). Draw the axis of symmetry that lies halfway between these points at x = 1. So, the x - coordinate of the vertex is (-2, 0) x = 1 and the y - coordinate of the vertex is: y = -(1 + 2)(1 - 4)= 9. (4, 0) x y

WRITING THE QUADRATIC EQUATION IN STANDARD FORM (1). y = -(x + 4)(x - 9) = -(x 2 - 9 x + 4 x - 36) = -(x 2 - 5 x -36) = -x 2 + 5 x + 36 (2). y = 3(x -1)2 + 8 = 3(x -1)(x - 1) + 8 = 3(x 2 - x + 1) + 8 = 3(x 2 - 2 x + 1) + 8 = 3 x 2 - 6 x + 3 + 8 = 3 x 2 - 6 x + 11

QUADRATIC FUNCTIONS IN REAL LIFE Researchers conducted an experiment to determine temperatures at which people feel comfortable. The percent of test subjects who felt comfortable at temperature x( in degrees Fahrenheit) can be modeled by: y = -3. 678 x 2 + 527. 3 x – 18, 807 a. What temperature made the greatest percent of test subjects comfortable? b. At that temperature , what percent felt comfortable?

SOLUTION Since a = -3. 678 is negative, the graph of the quadratic function open down and the function has a maximum value. The maximum value occurs at: The corresponding value of y is: a. b. Hence, The temperature that made the greatest percent of test subjects comfortable was about 72. At that temperature about 92% of the subjects felt comfortable.

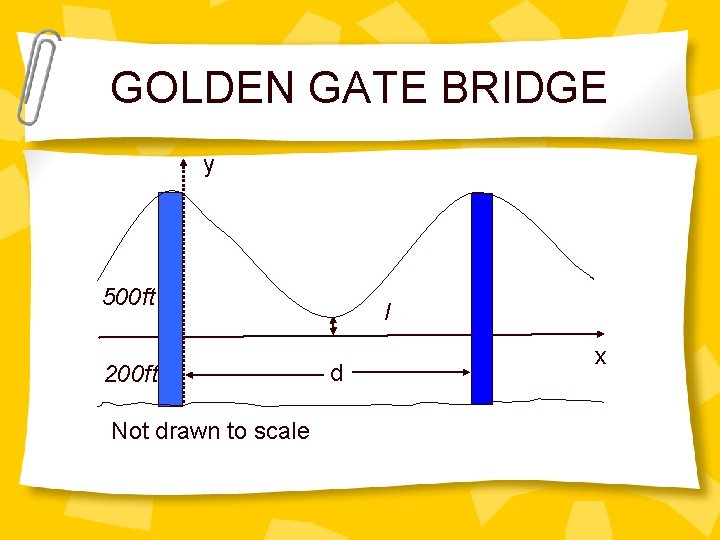
REAL LIFE EXAMPLE The Golden Gate Bridge in San Francisco has two towers that rise 500 feet above the road and are connected by suspension cables as shown. Each cable forms a parabola with equation where x and y are measured in feet. a. What is the distance d between the towers? b. What is the height l above the road of a cable at its lowest point?

GOLDEN GATE BRIDGE y 500 ft 200 ft Not drawn to scale l d x

SOLUTION Hence the vertex of the parabola is (2100, 8)

SOLUTION(contd. ) a. The vertex of the parabola is (2100, 8), so the cable’s lowest point is 2100 feet from the left tower shown above. Since the heights of the two tower’s are the same, the symmetry of the parabola implies that the vertex is also 2100 feet from the right tower. Therefore the towers are d = 2(2100) = 4200 feet apart. b. The height l above the road of a cable at its lowest point is the y-coordinate of the vertex. Since the vertex is (2100, 8), this height is l= 8 feet.

SOLVING QUADRATIC EQUATION BY FACTORING

FACTORING QUADRATIC EXPRESSION The expression x 2 + bx + c is a trinomial because it has three terms. We can use factoring to write it as product of two terms or binomials such as x 2 + bx + c = (x+m)(x+n) = x 2 + (m+n)x + mn Example: x 2 + 8 x + 15 = (x + 3)(x + 5)

EXAMPLE Problem: Factor x 2 - 12 x - 28 Solution: x 2 - 12 x - 28 = (x+m)(x+n) where mn = -28 and m+n = -12 Factors of -1, 28 1, -28 -2, 14 2, -14 -28 -27 12 -12 Sum of 27 factors The table shows that m = 2 and n = -14. So, x 2 - 12 x - 28 = (x + 2)(x - 14) -4, 7 4, -7 3 -3

SPECIAL FACTORING PATTERNS 1. Difference of two squares: a 2 - b 2 = (a+b)(a-b) Example: x 2 - 9 = (x+3)(x-3) 2. Perfect square Trinomial: a 2 + 2 ab + b 2 = (a+b)2 Example: x 2 + 12 x +36 = (x+6)2 3. Perfect square Trinomial: a 2 - 2 ab + b 2 = (a-b)2 Example: x 2 -8 x +16 = (x-4)2

FACTORING MONOMIALS FIRST Monomial is an expression that has only one term. Factor the quadratic expression: a. 5 x 2 - 20 = 5(x 2 -4) = 5(x+2)(x-2) b. 6 p 2 + 15 p + 9 = 3(2 p 2 + 5 p + 3) = 3(2 p + 3)(p + 1)

SOLVING QUADRATIC EQUATIONS Solve: The solution is 5. The solutions are -6 and 3.

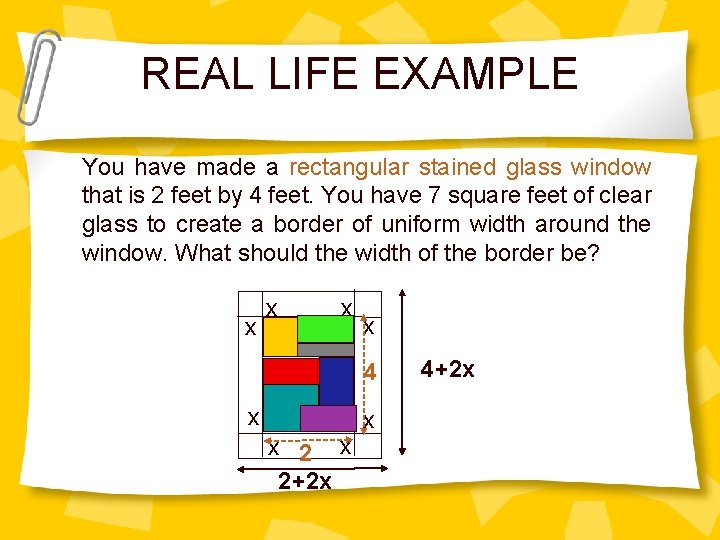
REAL LIFE EXAMPLE You have made a rectangular stained glass window that is 2 feet by 4 feet. You have 7 square feet of clear glass to create a border of uniform width around the window. What should the width of the border be? x x 4 x x 2+2 x x 4+2 x

SOLUTION Let the width of the border be = x Area of the border = 7 Area of the border and window = (2+2 x)(4+2 x) Area of the window = 2 4 = 8 Area of border = Area of border & window - Area of window 7 = (2+2 x)(4+2 x) - 8 0 = 4 x 2 + 12 x -7 0 = (2+7 x)(2 x-1) 2+7 x = 0 or 2 x-1 = 0 x = -3. 5 o x = 0. 5 Rejecting negative value, -3. 5. Hence the border’s width is 0. 5 ft

ZERO PRODUCT PROPERTY Let A and B be real numbers or algebraic expressions. If AB=0, then either A = 0 or B = 0 Solve (a) x 2 + 3 x -18 = 0 (x + 6)(x - 3) = 0. Hence either x + 6 = 0 or x - 3 = 0. The solutions are x = -6 or x = 3

ZERO PRODUCT PROPERTY Let A and B be real numbers or algebraic expressions. If AB=0, then either A = 0 or B = 0 Solve (a) 2 t 2 - 17 t + 45 = 3 t - 5 2 t 2 - 20 t + 50 = 0 t 2 - 10 t + 25 = 0 (t - 5)2 = 0 t - 5 = 0 t = 5 Hence the solutions is 5.

FINDING ZEROES OF QUADRATIC FUNCTIONS Find zeros of y = x 2 -x -6 Solution: y = x 2 - 3 x + 2 x - (3 2) y = x(x-3) + 2(x-3) y = (x + 2)(x - 3) Hence the zeros of the function are -2 and 3.

SOLVING QUADRATIC EQUATIONS BY FINDING SQUARE ROOTS

SQUARE ROOT

PROPERTIES OF SQUARE ROOTS (a>0, b>0) PRODUCT PROPERTY: QUOTIENT PROPERTY:

SIMPLIFY

Solving a quadratic equation Solve: Hence the solutions are: and

REAL LIFE EXAMPLE A stunt man working on the set of a movie is to fall out of a window 100 feet above the ground. For the stunt man’s safety, an air cushion 26 feet wide by 30 feet long by 9 feet high is positioned on the ground below the window. a. For how many seconds will the stunt man fall before he reaches the cushion? b. A movie camera operating at a speed of 24 frames per second records the stunt man’s fall. How many frames of film show the stunt man falling?

SOLUTION a. The stunt man’s initial height is ho = 100 feet, so his height as a function of time can be modeled by function h = -16 t 2 + 100. Since the height of the cushion is 9 feet above the ground, the time taken by the stunt man to reach the cushion is: h = -16 t 2 + 100 9 = -16 t 2 + 100 -91 = -16 t 2 91/16 = t 2 or t ≈ 2. 4. b. Thus, it takes about 2. 4 seconds for the stunt man to reach the cushion. c. The number of frames of film that show the stunt man falling is given by the product (2. 4 sec)(24 frames/sec), or about 57 frames.

COMPLEX NUMBERS

COMPLEX NUMBER A complex number written in standard form is a number a+bi where a and b are real numbers. The number a is the real part of the complex number and number bi is the imaginary part. If b≠ 0, then a+bi is an imaginary number. If a=0 and b≠ 0, then a+bi is a pure imaginary number. A complex plane has a horizontal axis called the real axis and a vertical axis called the imaginary axis.

THE SQUARE ROOT OF A NEGATIVE NUMBER 1. If r is a positive real number, then where i is the imaginary unit defined as 2. By property (1), it follows that

Complex Number Cycle

SOLVING A QUADRATIC EQUATION Solve: Hence, the solutions are and

PLOTTING COMPLEX NUMBERS y Plot 2 -3 i in the complex plane. To plot 2 -3 i , start at the origin, move 2 units to the right and then move 3 units down. 0 x 2 -3 i

ADDING AND SUBTRACTING COMPLEX NUMBERS Sum of complex numbers: Difference of complex numbers: (a+bi) + (c+di) = (a+c) + i(b+d) (a+bi) - (c+di) = (a-c) + i(b-d) Example: (4 -i) + (3+2 i) = (4+3) + i(-1+2) = 7 + i Example: (7 -5 i) - (1 -5 i) = (7 -1) + i(-5+5) = 6 + 0 i = 6

MULTIPLYING THE COMPLEX NUMBERS Write the expression as a complex number in standard form. a. 5 i(-2+i) = -10 i + 5 i 2 = -10 i + 5(-1) = -5 -10 i b. (7 -4 i)(-1+2 i) = -7 + 14 i + 4 i - 8 i 2 = -7 + 18 i - 8(-1) = 1 + 18 i

DIVIDING COMPLEX NUMBERS Write the quotient in standard form. Solution: Multiply the numerator and denominator by the complex conjugate of the denominator.

ABSOLUTE VALUES OF COMPLEX NUMBER Find the absolute value of each complex number.

THE QUADRATIC FORMULA AND THE DISCRIMINANT

THE QUADRATIC FORMULA Let a, b, and c be real numbers such that a≠ 0. The solutions of the quadratic equation ax 2 + bx +c = 0 are:

SOLVING QUADRATIC EQUATION WITH TWO REAL SOLUTIONS The solutions are:

SOLVING QUADRATIC EQUATION WITH ONE REAL SOLUTIONS Hence, the solution is 3.

SOLVING QUADRATIC EQUATION WITH TWO IMAGINARY SOLUTIONS The solutions are: 1+i and 1 -i

DISCRIMINANT In the quadratic formula, the expression b 2 -4 ac under the radical sign is called the discriminant of the associated equation ax 2 + bx + c = 0.

NUMBER AND TYPE OF SOLUTIONS OF A QUADRATIC EQUATION Consider the quadratic equation ax 2 + bx + c = 0. If b 2 -4 ac > 0, then the equation has two real solutions. If b 2 -4 ac = 0, then the equation has one real solutions. If b 2 -4 ac < 0, then the equation has two imaginary solutions.

EXAMPLE: TWO REAL SOLUTIONS Hence there are two real solutions: 4, 2

EXAMPLE: ONE REAL SOLUTION Hence, there is one real solution: 3

EXAMPLE: TWO IMAGINARY SOLUTIONS Find the discriminant of the quadratic equation and give the number and type of solutions of the equation. Hence there are two imaginary solutions: 3+i and 3 -i

REAL LIFE EXAMPLE A baton twirler tosses a baton into the air. The baton leaves the twirler’s hand 6 feet above the ground and has an initial vertical velocity of 45 feet per second. The twirler catches the baton when it falls back to a height of 5 feet. For how long is the baton in the air? Solution: Since the baton is thrown, we use the model h = -16 t 2 + vot + ho where vo = 45, ho = 6, h = 5.

SOLUTION(contd. ) Rejecting the negative solution, the baton is in the air for about 2. 8 seconds.

GRAPHING AND SOLVING QUADRATIC INEQUALITIES

GRAPHING A QUADRATIC INEQUALITY IN TWO VARIABLES y < ax 2 +bx +c y ≤ ax 2 +bx +c y > ax 2 +bx +c y ≥ ax 2 +bx +c Draw parabola with equation y = ax 2 +bx +c. Make the parabola dashed for inequalities with < or > and solid for inequalities with ≤ or ≥. Choose a point (x, y) inside the parabola and check whether the point is a solution of the inequality. If a point (x, y) is a solution, shade the region inside the parabola. If it is not the solution, shade the region outside the parabola.

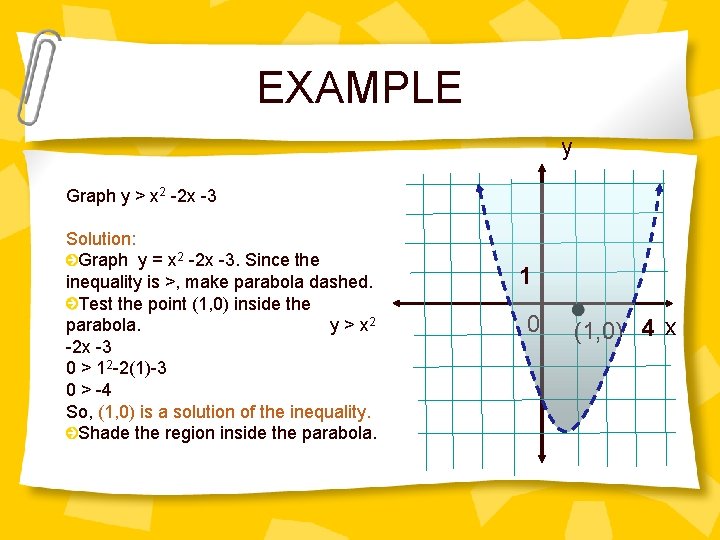
EXAMPLE y Graph y > x 2 -2 x -3 Solution: Graph y = x 2 -2 x -3. Since the inequality is >, make parabola dashed. Test the point (1, 0) inside the parabola. y > x 2 -2 x -3 0 > 12 -2(1)-3 0 > -4 So, (1, 0) is a solution of the inequality. Shade the region inside the parabola. 1 0 (1, 0) 4 x

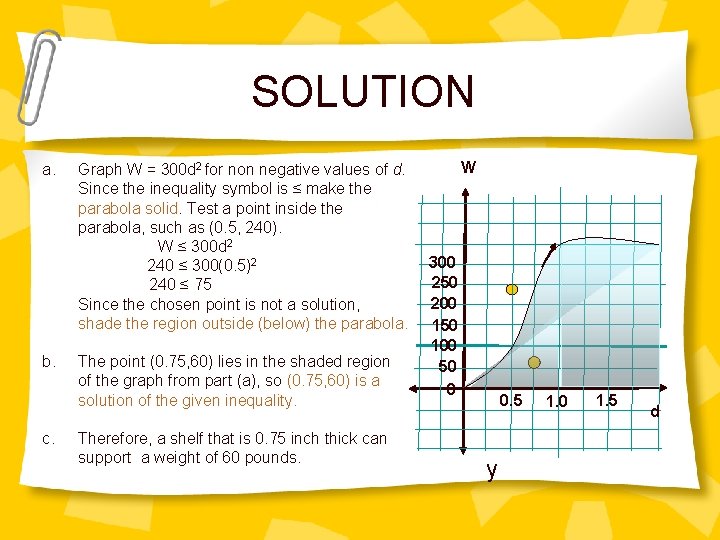
REAL LIFE EXAMPLE You are building a wooden bookcase. You want to choose a thickness d(in inches) for the shelves so that each is strong enough to support 60 pounds of books without breaking. A shelf can safely support a weight of W ( in pounds) provided that W ≤ 300 d 2 a. Graph the given inequality b. If you make each shelf 0. 75 inch thick, can it support a weight of 60 pounds?

SOLUTION a. b. c. Graph W = 300 d 2 for non negative values of d. Since the inequality symbol is ≤ make the parabola solid. Test a point inside the parabola, such as (0. 5, 240). W ≤ 300 d 2 240 ≤ 300(0. 5)2 240 ≤ 75 Since the chosen point is not a solution, shade the region outside (below) the parabola. The point (0. 75, 60) lies in the shaded region of the graph from part (a), so (0. 75, 60) is a solution of the given inequality. Therefore, a shelf that is 0. 75 inch thick can support a weight of 60 pounds. W 300 250 200 150 100 50 0 0. 5 y 1. 0 1. 5 d

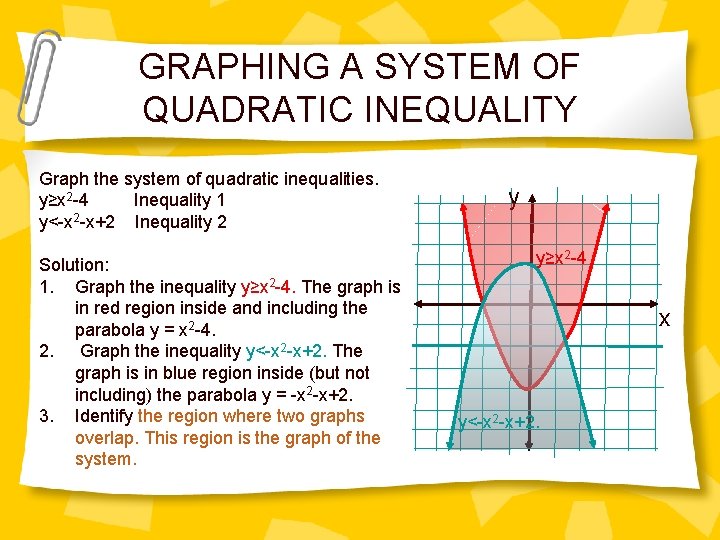
GRAPHING A SYSTEM OF QUADRATIC INEQUALITY Graph the system of quadratic inequalities. y≥x 2 -4 Inequality 1 y<-x 2 -x+2 Inequality 2 Solution: 1. Graph the inequality y≥x 2 -4. The graph is in red region inside and including the parabola y = x 2 -4. 2. Graph the inequality y<-x 2 -x+2. The graph is in blue region inside (but not including) the parabola y = -x 2 -x+2. 3. Identify the region where two graphs overlap. This region is the graph of the system. y y≥x 2 -4 x y<-x 2 -x+2.

QUADRATIC INEQUALITY IN ONE VARIABLE 1. To solve ax 2 + bx + c < 0 (or ax 2 + bx + c ≤ 0), graph y = ax 2 + bx + c and identify the x values for which the graph lies below (or on and below) the x-axis. 2. To solve ax 2 + bx + c > 0 (or ax 2 + bx + c ≥ 0), graph y = ax 2 + bx + c and identify the x values for which the graph lies above (or on and below) the x-axis.

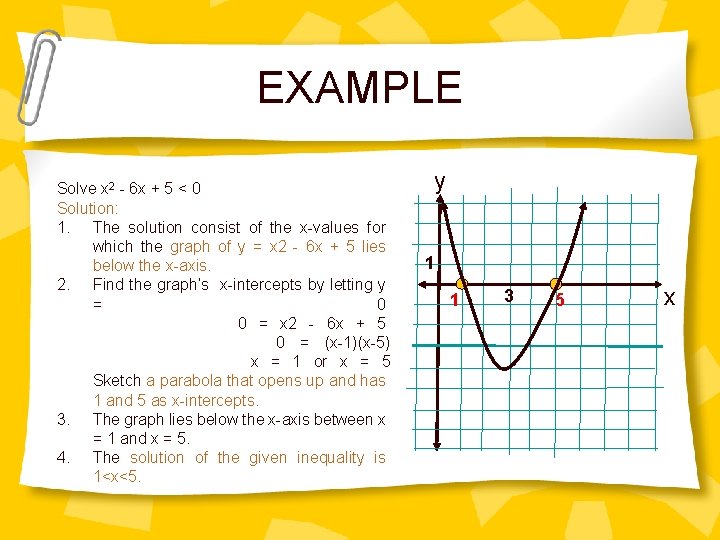
EXAMPLE Solve x 2 - 6 x + 5 < 0 Solution: 1. The solution consist of the x-values for which the graph of y = x 2 - 6 x + 5 lies below the x-axis. 2. Find the graph’s x-intercepts by letting y = 0 0 = x 2 - 6 x + 5 0 = (x-1)(x-5) x = 1 or x = 5 Sketch a parabola that opens up and has 1 and 5 as x-intercepts. 3. The graph lies below the x-axis between x = 1 and x = 5. 4. The solution of the given inequality is 1<x<5. y 1 1 3 5 x

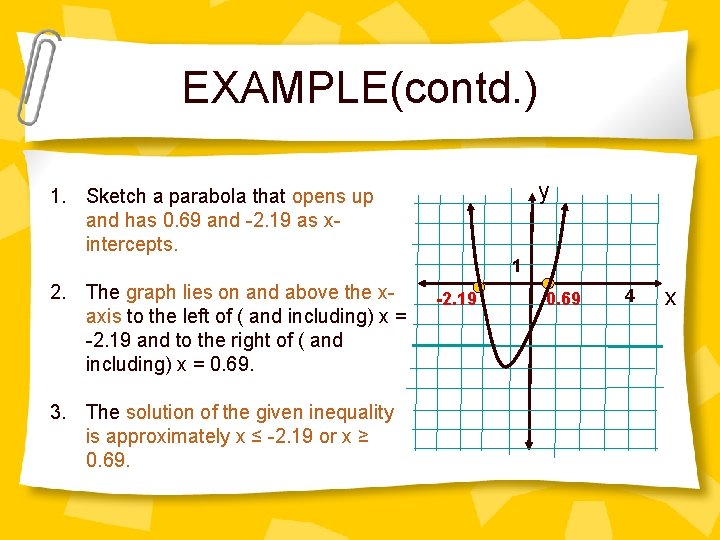
EXAMPLE Solve 2 x 2 + 3 x -3 ≥ 0 Solution: 1. The solution consist of the x-values for which the graph of y = 2 x 2 + 3 x -3 lies on and above the x-axis. 2. Find the graph’s x-intercepts by letting y = 0 0 = 2 x 2 + 3 x -3

EXAMPLE(contd. ) y 1. Sketch a parabola that opens up and has 0. 69 and -2. 19 as xintercepts. 1 2. The graph lies on and above the xaxis to the left of ( and including) x = -2. 19 and to the right of ( and including) x = 0. 69. 3. The solution of the given inequality is approximately x ≤ -2. 19 or x ≥ 0. 69. -2. 19 0. 69 4 x

SOLVING A QUADRATIC INEQUALITY ALGEBRAICALLY Solve: x 2 + 2 x ≤ 8 Solution: First replace the inequality symbol with equal sign. x 2 + 2 x = 8 x 2 + 2 x - 8 = 0 (x+4)(x-2) = 0 x = - 4 or x = 2 The numbers -4 and 2 are the critical x-values of the inequality x 2 + 2 x ≤ 8. Plot -4 and 2 on a number line.

SOLUTION (contd. ) -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 These critical x-values partition the number line into three intervals. Test x = -5, (-5)2 + 2(-5) = 15 ≤ 8 Test x = 0, (0)2 +2(0) = 0 ≤ 8 Test x = -3, (3)2 + 2(3) = 15 ≤ 8 Hence the solution is -4 ≤ x ≤ 2.

REAL LIFE EXAMPLE For a driver aged x years, a study found that the driver’s reaction time V(x) (in milliseconds) to a visual stimulus such as traffic can be modeled by: V(x) = 0. 005 x 2 - 0. 23 x + 22, 16 ≤ x ≤ 70 At what ages does a driver’s reaction time tend to be greater than 25 milliseconds? Solution: The values of x for which V(x) > 25 0. 005 x 2 - 0. 23 x +22 > 25 0. 005 x 2 - 0. 23 x - 3 > 0 The solution consists of the x- values for which the graph lies above the xaxis.

SOLUTION(contd. ) The graph’s x intercept is found by letting y =0 and using the quadratic formula to solve for x. 0. 005 x 2 - 0. 23 x - 3 = 0 Rejecting the negative value, the graph’s x-intercept is about 57. The graph of 0. 005 x 2 - 0. 23 x - 3 = 0 lies in the domain 16 ≤ x ≤ 70. The graph lies above the x-axis when 57 < x ≤ 70. Hence the drivers over 57 years old tend to have reaction times greater than 25 milliseconds.

MODELING WITH QUADRATIC FUNCTIONS

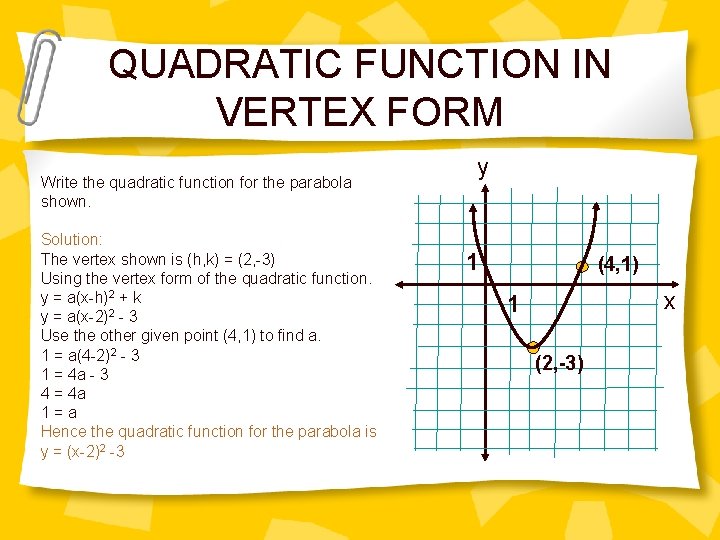
QUADRATIC FUNCTION IN VERTEX FORM Write the quadratic function for the parabola shown. Solution: The vertex shown is (h, k) = (2, -3) Using the vertex form of the quadratic function. y = a(x-h)2 + k y = a(x-2)2 - 3 Use the other given point (4, 1) to find a. 1 = a(4 -2)2 - 3 1 = 4 a - 3 4 = 4 a 1 = a Hence the quadratic function for the parabola is y = (x-2)2 -3 y 1 (4, 1) x 1 (2, -3)

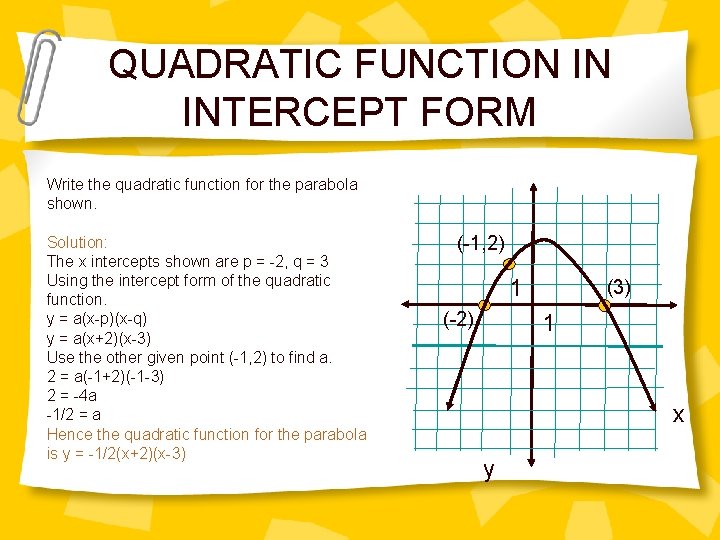
QUADRATIC FUNCTION IN INTERCEPT FORM Write the quadratic function for the parabola shown. Solution: The x intercepts shown are p = -2, q = 3 Using the intercept form of the quadratic function. y = a(x-p)(x-q) y = a(x+2)(x-3) Use the other given point (-1, 2) to find a. 2 = a(-1+2)(-1 -3) 2 = -4 a -1/2 = a Hence the quadratic function for the parabola is y = -1/2(x+2)(x-3) (-1, 2) 1 (-2) (3) 1 x y

END