Quadratic Equations and Quadratic Functions Vocabulary Quadratic function

Quadratic Equations and Quadratic Functions

• • Vocabulary Quadratic function. Quadratic term. Linear term. Constant term. Parabola- the graph of a quadratic function Axis of Symmetry- a line that makes the parabola symmetric • Vertex- the minimum or maximum point of the parabola • Zeros- the x-intercepts of the parabola

Identify the quadratic term, the linear term, and the constant term. 1) 2) 3)

Solving Quadratic Equations by Factoring Objective: 1) To solve problems by factoring

Solve by using he zero product property by factoring 1) 2) 3)

The Quadratic Formula and the Discriminant Objective: 1) To solve quadratic equations by using the quadratic formula 2) To use the discriminant to determine the nature of the roots of quadratic equations

Quadratic Equations ax 2+bx+c=0 1. Solve by: The Quadratic formula

Quadratic Functions Vertex form Axis of symmetry is x=h Vertex is (h, k) a>0 parabola opens up and has minimum a<0 parabola opens down and has maximum |a|>1 parabola is narrow |a|<1 parabola is wide and solve General Form Axis of symmetry is Vertex is a>0 parabola opens up and has minimum a<0 parabola opens down and has maximum |a|>1 parabola is narrow |a|<1 parabola is wide

Use quadratic formula to solve each equation. (1. )

Use quadratic formula to solve each equation. (2. )

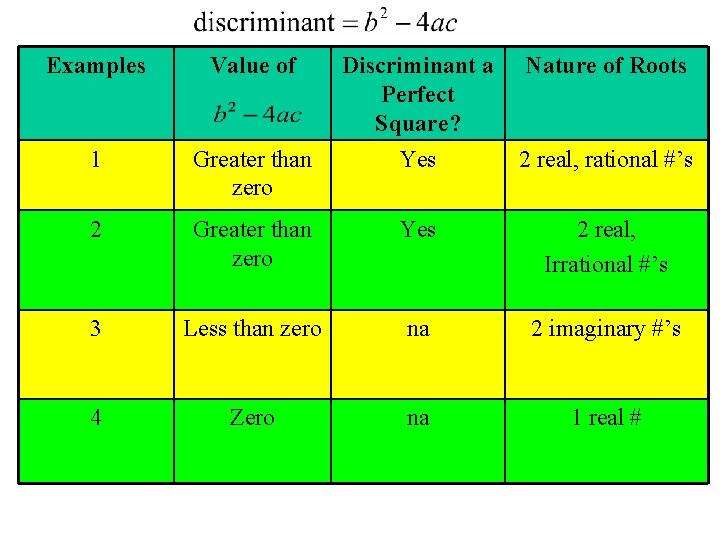
Examples Value of Discriminant a Perfect Square? Nature of Roots 1 Greater than zero Yes 2 real, rational #’s 2 Greater than zero Yes 2 real, Irrational #’s 3 Less than zero na 2 imaginary #’s 4 Zero na 1 real #

Find the value of the discriminant for each quadratic equation. Then describe the nature of the roots. 3) 4)

Find the value of the discriminant for each quadratic equation. Then describe the nature of the roots. 5) 6)

Vertex to Standard Form Notes

Change quadratic functions to standard form Rewrite (x+1)² Multiply using FOIL Don’t forget your +2 Combine like terms Standard Form

Compare Vertex vs. Standard Vertex form: Standard form: Lets look at our last problem We converted to a=1 h = -1 k=2 a=1 b=2 Compare values c=3

Lets try this one! Write the quadratic function in standard form. Label the values for a, b, and c.

Your Turn Write the quadratic function in standard form. Label the values for a, b, and c.