QUADRATIC EQUATIONS QUADRATIC EQUATIONS DEFINITION OF QUADRATIC EXPRESSION

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS DEFINITION OF QUADRATIC EXPRESSION, EQUATION & ITS ROOTS

QUADRATIC EQUATIONS Quadratic Expression: We know that quadratic means 2+bx+c, degree ‘ 2’ A polynomial of the form ax where a, b, c are complex numbers and a 0 variable ‘x’. Example: is called a quadratic expression in the

QUADRATIC EQUATIONS Quadratic Equation : a, b, c are complex numbers An equation of the form ax 2+bx+c where =0 and a 0 is called a quadratic equation in the variable ‘x’. The numbers a, b, c are called the coefficients of this Here ‘a’ is called leading equation. coefficient of the equation Example:

QUADRATIC EQUATIONS Zero of a Quadratic Expression : A complex number ‘ ’ is said to be a zero of the quadratic expression if a 2+b +c=0 ax 2+bx+c Example: 1 and 2 are zeros of the quadratic expression x 2 -3 x+2

QUADRATIC EQUATIONS Roots of a Quadratic Equation: A complex number ‘ ’ is said to be a root or solution of the quadratic if a 2+b +c=0. equation ax 2+bx+c=0, Example: ‘ 2’ is the root of a quadratic equation x 2 -3 x+2=0. Note: The zeros of the quadratic expression ax 2+bx+c are the same as the roots of the quadratic equation ax 2+bx+c=0.

QUADRATIC EQUATIONS Theorem: Proof: If ‘ ’ is a root of the quadratic equation ax 2+bx+c=0 a 2+b +c=0 4 a(a 2+b +c)=0 4 a 2 2+4 ab +4 ac=0 then

QUADRATIC EQUATIONS (2 a )2+2. (2 a ). b = -4 ac 2=b 2 -4 ac (2 a )2 Adding +2. (2 a ). b+b 2’ ‘b on both sides (2 a +b)2=b 2 -4 ac

QUADRATIC EQUATIONS Note: 1) A quadratic equation ax 2+bx+c=0 has two roots (real or complex, not necessarily distinct) 2) If both roots of the quadratic equation are equal to ,

QUADRATIC EQUATIONS VERY SHORT ANSWER QUESTIONS 1. Find the roots of the equation 3 x 2+2 x-5=0 Solution Here a=3, b=2, c=-5 The roots of the given equation are

QUADRATIC EQUATIONS We can also obtain these roots in the following way

QUADRATIC EQUATIONS 2. Find the roots of 4 x 2 -4 x+17= 3 x 2 -10 x-17 Solution: 4 x 2 -4 x+17= 3 x 2 -10 x-17 x 2+6 x+34= 0 Here a=1, b=6, c=34 The roots of the given equation are

QUADRATIC EQUATIONS = -3 +5 i, -3 -5 i Hence, the roots of the given equation are -3+5 i, -3 -5 i

QUADRATIC EQUATIONS Solution The roots of the given equation are

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS NATURE OF ROOTS & APPLICATIONS

QUADRATIC EQUATIONS Nature of the roots of a Quadratic Equation: Definition: ‘b 2 -4 ac’ is called the discriminant of the quadratic equation ax 2+bx+c=0. And it is denoted by the symbol “ ” or “ D ”. To discuss the nature of the roots, consider the following cases :

QUADRATIC EQUATIONS Let , be the roots of the quadratic equation ax 2+bx+c=0 Case I: If a, b, c are real numbers, then (i) >0 and are real and distinct (iii) <0 and are non-real complex numbers conjugate to each other.

QUADRATIC EQUATIONS Case II: If a, b, c are rational numbers, then (i) =0 and are rational and equal (ii) >0 and is perfect square and are rational and distinct. (iii) >0 and is not a perfect square and are irrational and distinct ( conjugate surds ) (iv) <0 and are imaginary numbers and conjugate to each other.

QUADRATIC EQUATIONS 1. Find the nature of the roots of the equation 4 x 2 -20 x+25=0 without finding the roots. Solution Here a=4, b=-20, c=25 b 2 -4 ac = 400 - 4(4)(25) = 0 Hence, the given equation has rational and equal roots.

QUADRATIC EQUATIONS 2. Show that the equation 2 x 2 -6 x+7=0 has no real root. Solution Here a=2, b=-6, c=7 b 2 -4 ac = (-6)2 - 4(2)(7) = -20 <0 The given equation has no real root.

QUADRATIC EQUATIONS 3. Show that the roots of (x-a)(x-b)=h 2 are always real. Solution Given equation can be written as x 2 -(a+b)x+ab-h 2=0 comparing with Ax 2+Bx+C=0 Here A=1, B=-(a+b), C=ab-h 2 B 2 -4 AC = (a+b)2 - 4(1)(ab-h 2) = (a+b)2 – 4 ab+4 h 2 = (a-b)2 + 4 h 2 0 The roots of given equation are always real.

QUADRATIC EQUATIONS 4. If x 2 -15 -m(2 x-8)=0 has equal roots, find ‘m’. Solution Given equation can be written as x 2 -2 mx+(8 m-15)=0 Here, a=1, b=-2 m, c=8 m-15 b 2 -4 ac = 0 (since the roots of given equation are equal) 2 – 4(1)(8 m-15) equation ax +bx+c=0= 0 i. e. , If the (-2 m) has equal roots, b 2 -4 ac=0 2 4 m – 32 m + 60 = 0 m 2 – 8 m + 15 = 0 (m-3)(m-5) = 0 m = 3 (or) 5 2

QUADRATIC EQUATIONS 5. If c 2 ab and the roots of (c 2 -ab)x 2 -2(a 2 -bc)x+(b 2 -ac)=0 are equal, then show that a=0 (or) a 3+b 3+c 3=3 abc. Solution Given equation (c 2 -ab)x 2 -2(a 2 -bc)x+(b 2 -ac)=0 comparing with Ax 2+Bx+C=0 Here, A=(c 2 -ab), B=-2(a 2 -bc), C=(b 2 -ac) B 2 -4 AC=0(since the roots are equal)

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS PROBLEMS ON SUM & PRODUCT OF THE ROOTS OF Q. E

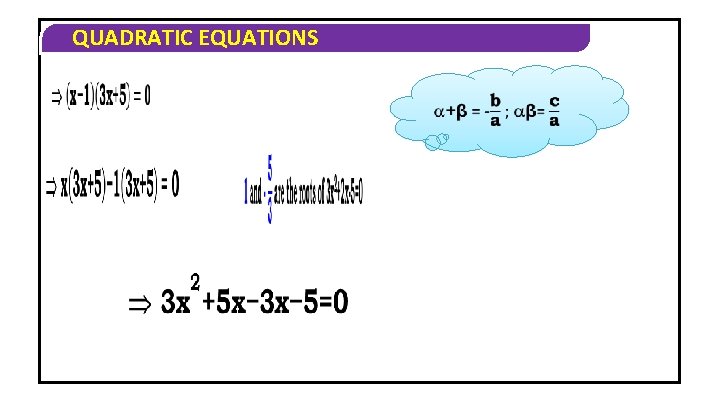
QUADRATIC EQUATIONS Note 1. If and are the roots of ax 2+bx+c=0 then + =-b/a and =c/a Proof Since the roots of ax 2+bx+c=0 are

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS Note 2. If and are the roots of ax 2+bx+c=0 then ax 2+bx+c=a(x- ) Proof + =-b/a =c/a

QUADRATIC EQUATIONS 3. The quadratic equation having roots , is i. e. , x 2 -( + )x+ =0 ⇒ x 2 -(sum of the roots)x+(product of the roots) = 0 (x- )=0

QUADRATIC EQUATIONS 1. If , are the roots of ax 2+bx+c=0, then find the value of 3+ 3 Solution

QUADRATIC EQUATIONS Solution

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 3. If , are the roots of ax 2+bx+c=0, then find the value of 4 7+ 7 4 Solution

QUADRATIC EQUATIONS Solution The quadratic equation having roots , is x 2( + )x+ =0

QUADRATIC EQUATIONS =4, =1 The quadratic equation having roots , is x 2( + )x+ =0

QUADRATIC EQUATIONS Thank you…