4 1 Graph Quadratic Functions in Standard Form









- Slides: 11

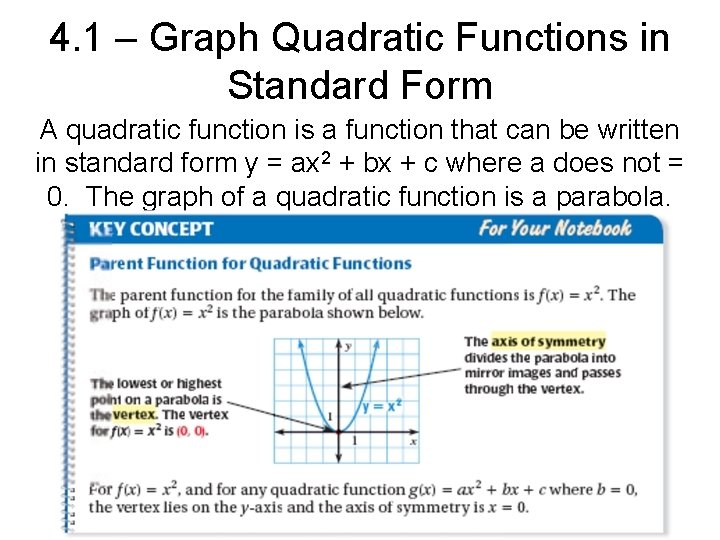
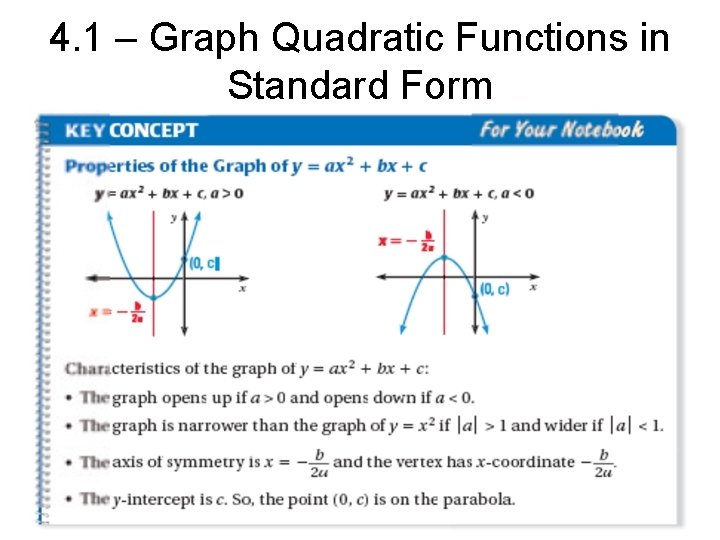
4. 1 – Graph Quadratic Functions in Standard Form A quadratic function is a function that can be written in standard form y = ax 2 + bx + c where a does not = 0. The graph of a quadratic function is a parabola.

4. 1 – Graph Quadratic Functions in Standard Form Example 1: Graph a function of the form y = ax 2 Graph y = 2 x 2. Compare the graph with the graph of y = x 2

4. 1 – Graph Quadratic Functions in Standard Form Example 2: Graph a function of the form y = ax 2 Graph y = ½x 2. Compare the graph with the graph of y = x 2

4. 1 – Graph Quadratic Functions in Standard Form Example 3: Graph a function of the form y = ax 2+c Graph y = -½x 2 + 3. Compare the graph with the graph of y = x 2

4. 1 – Graph Quadratic Functions in Standard Form

4. 1 – Graph Quadratic Functions in Standard Form Example 4: Graph a function of the form y = ax 2+bx+c Graph y = 2 x 2 - 8 x + 2.

4. 1 – Graph Quadratic Functions in Standard Form Example 5: Graph a function of the form y = ax 2+bx+c Graph y = 3 x 2 +9 x – 7.

4. 1 – Graph Quadratic Functions in Standard Form

4. 1 – Graph Quadratic Functions in Standard Form Example 6: Tell whether the function y = 3 x 2 – 18 x + 20 has a minimum value or a maximum value. Then find the min or max value.

4. 1 – Graph Quadratic Functions in Standard Form Example 6: A go-cart track has about 380 racers per week and charges each racer $35 to race. The owner estimates that there will be 20 more racers per week for every $1 reduction in price per racer. How can the owner of the go-cart track maximize weekly revenue?

4. 1 – Graph Quadratic Functions in Standard Form Example 6: An electronics store sells about 70 of a new model of digital camera per month at a price of $320 each. For each $20 decrease in price, about 5 more cameras per month are sold. Write a function that models the situation. Then tell how the store can maximize monthly revenue from sales of the camera.