Quadratic Graphs and Their Properties Quadratic Functions n

Quadratic Graphs and Their Properties. Quadratic Functions. n r a e l l l ’ u o ty a h W To graph quadratic functions of the form To identify the axis of symmetry, vertex, domain. range and intercept(s) for a given parabola. To graph quadratic functions of the form y Quadratic function, Standard form, r a l u b a c o V Parent function, parabola, axis of symmetry, vertex, minimum, maximum

Take a Note: A quadratic function is a function that can be written in the form This form is called the standard form of a quadratic function. Examples: The simplest quadratic function the quadratic parent function. is The graph od the quadratic function is called parabola and has a U shape. You can fold a parabola so that the two sides match exactly. The fold or line that divides the parabola into matching halves is called the axis of symmetry.

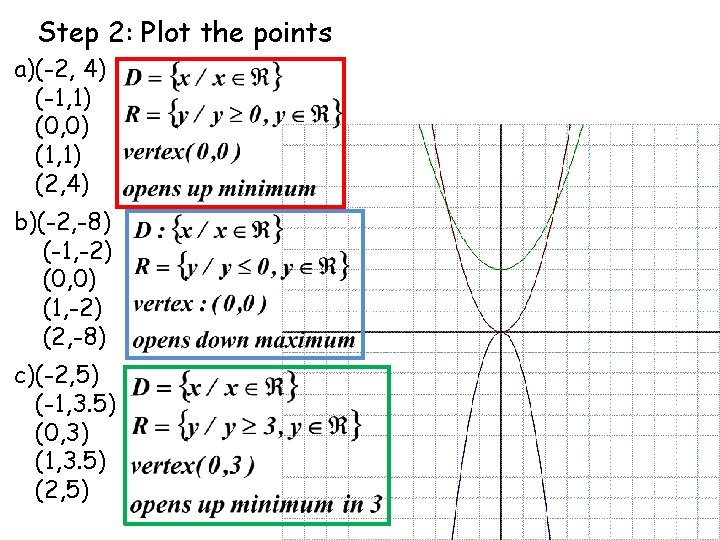
Problem 1: Graphing a Quadratic. Identifying a vertex. Graph. Step 1: Make a table. X -2 4 -1 1 0 0 1 1 2 4 3 9

Step 2: Plot the points a)(-2, 4) (-1, 1) (0, 0) (1, 1) (2, 4) b)(-2, -8) (-1, -2) (0, 0) (1, -2) (2, -8) c)(-2, 5) (-1, 3. 5) (0, 3) (1, 3. 5) (2, 5)

Take a note: The highest or the lowest point of a parabola is a vertex, which is on the axis of symmetry

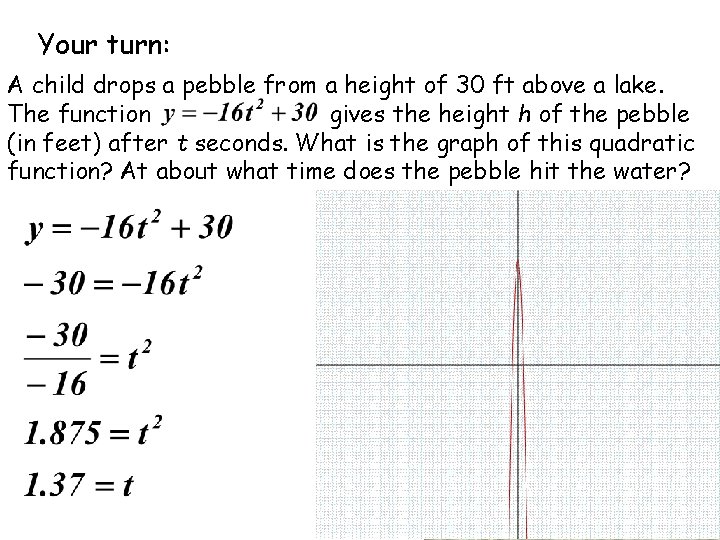
Your turn: A child drops a pebble from a height of 30 ft above a lake. The function gives the height h of the pebble (in feet) after t seconds. What is the graph of this quadratic function? At about what time does the pebble hit the water?

Take a note: There is another way to graph a parabola . The graph of has the line as its axis of as symmetry . , where The x-coordinate of the vertex is and the y-coordinate of the vertex is . You can use the coordinates of the vertex, the axis of symmetry and the y-intercept (meaning when x=0)to help you graph a quadratic function.

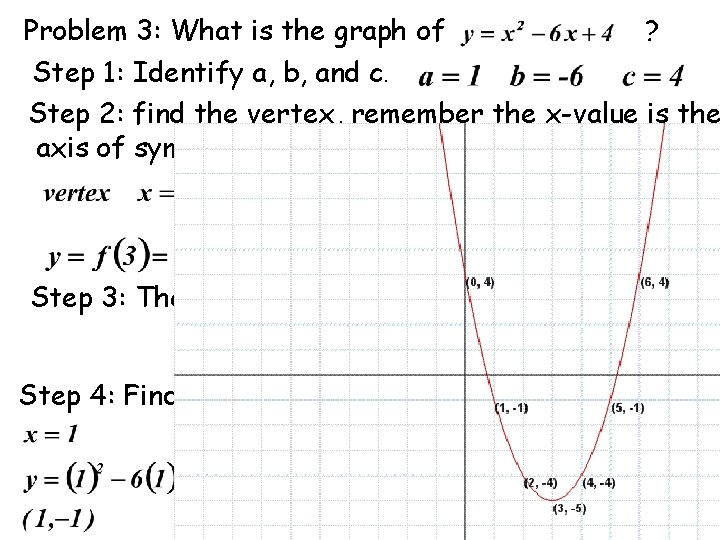
Problem 3: What is the graph of ? Step 1: Identify a, b, and c. Step 2: find the vertex, remember the x-value is the axis of symmetry. Step 3: The y-intercept Step 4: Find another point in the side as the vertex.

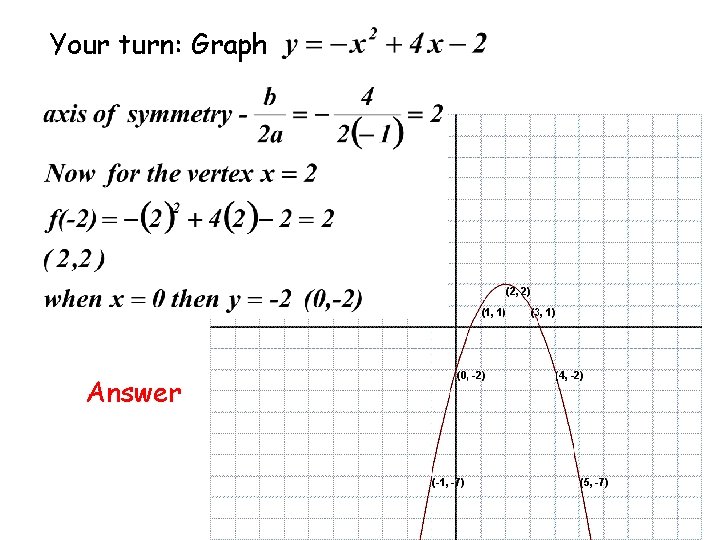
Your turn: Graph Answer

Problem 4: A baseball is thrown into the air with an upward velocity of 30 ft/s. Its height h, in feet, after t seconds is given by the function. How long will take the ball to reach its maximum height? What is the ball’s maximum height? What is the range of the function? Answer

Your turn: During a halftime basketball game, a slingshot launches T-shirts at the crowd. A T-shirt is launched with an Initial velocity of 72 ft/sec. The T-shirt is caught 35 ft. above the court. How long will take the T-shirt to reach its maximum height? What is the range of the function that models the height of the T-shirt over time? Answer

Classwork odd Homework even TB pgs. 538 -539 exercises. 7 -48 pgs. 544 -545 exercises 7 -33