Lesson 9 3 Transformations of Quadratic Functions Transformation

Lesson 9 -3: Transformations of Quadratic Functions

Transformation • A transformation changes the position or size of a figure • 3 types of transformations: 1. Translations 2. Dilations 3. Reflections

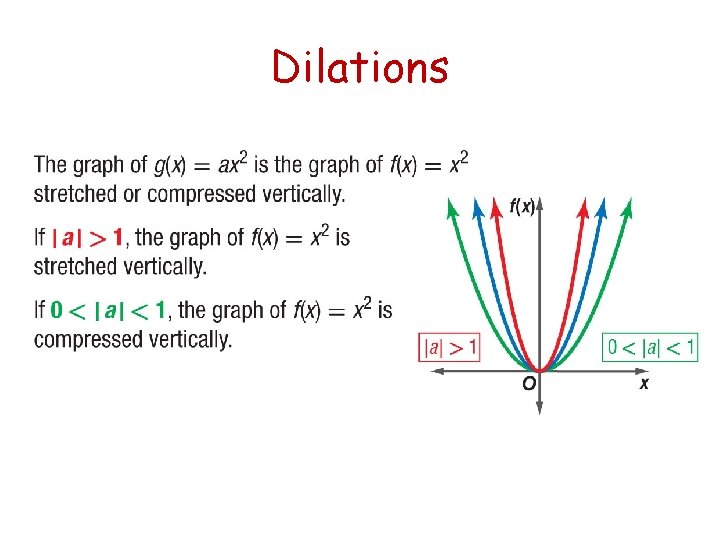
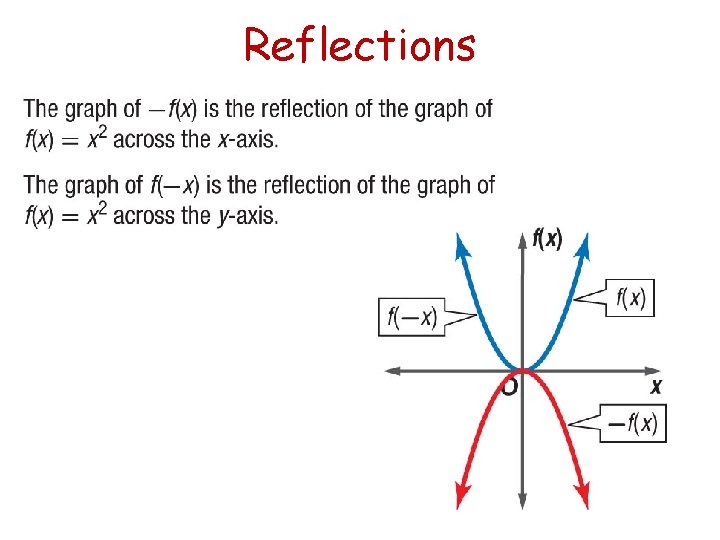
Vocabulary A dilation is a transformation that makes the graph narrower or wider than the parent graph. A reflection flips a figure over the x-axis or y-axis.

Dilations

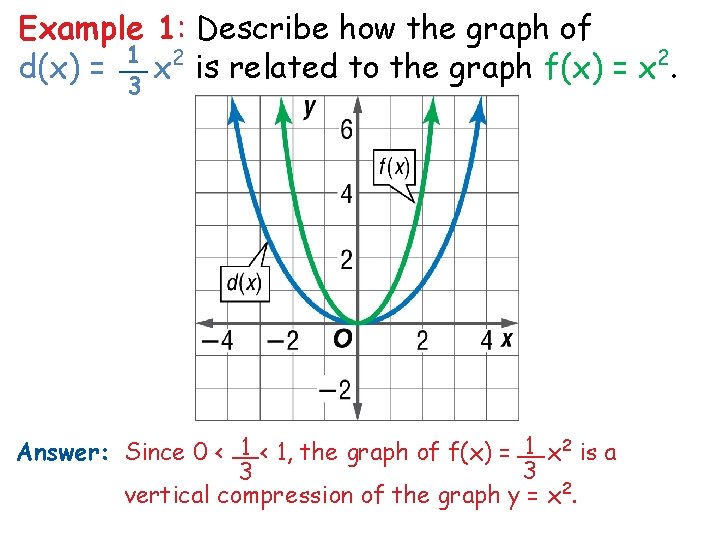
Example 1: Describe how the graph of 1 2 __ d(x) = x is related to the graph f(x) = x 2. 3 1 x 2 is a 1 < 1, the graph of f(x) = __ Answer: Since 0 < __ 3 3 vertical compression of the graph y = x 2.

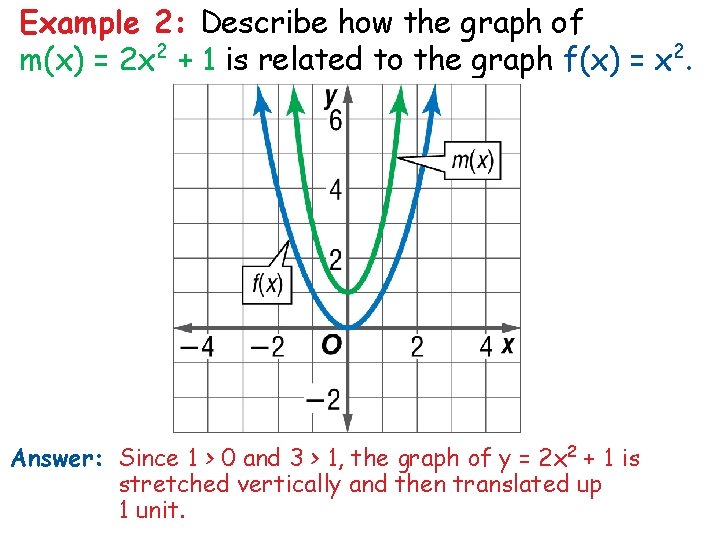
Example 2: Describe how the graph of m(x) = 2 x 2 + 1 is related to the graph f(x) = x 2. Answer: Since 1 > 0 and 3 > 1, the graph of y = 2 x 2 + 1 is stretched vertically and then translated up 1 unit.

Example 3: Describe how the graph of n(x) = 2 x 2 is related to the graph of f(x) = x 2. A. n(x) is compressed vertically from f(x). B. n(x) is translated 2 units up from f(x). C. n(x) is stretched vertically from f(x). D. n(x) is stretched horizontally from f(x).

Example 4: Describe how the graph of 1 2 b(x) = __ x – 4 is related to the graph of f(x) = x 2. 2 A. b(x) is stretched vertically and translated 4 units down from f(x). B. b(x) is compressed vertically and translated 4 units down from f(x). C. b(x) is stretched horizontally and translated 4 units up from f(x). D. b(x) is stretched horizontally and translated 4 units down from f(x).

Reflections

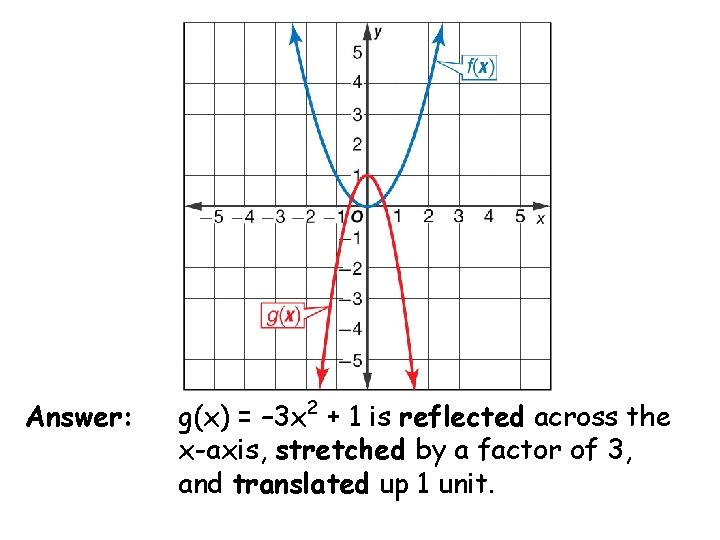
Example 1: How is the graph of g(x) = – 3 x 2 + 1 related to the graph of f(x) = x 2 ? Three transformations are occurring: 1. First, the negative sign causes a reflection across the x-axis. 2. Then a dilation occurs, where a = 3. 3. Last, a translation occurs, where h = 1.

Answer: g(x) = – 3 x 2 + 1 is reflected across the x-axis, stretched by a factor of 3, and translated up 1 unit.

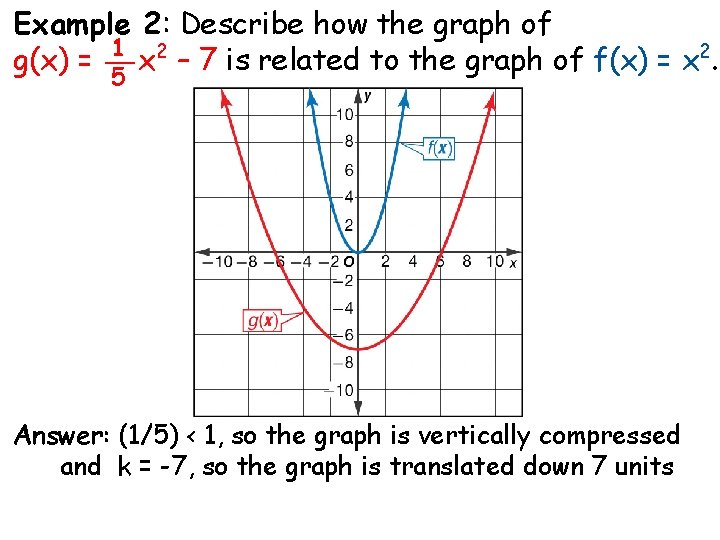
Example 2: Describe how the graph of 1 2 2 g(x) = __ x – 7 is related to the graph of f(x) = x. 5 Answer: (1/5) < 1, so the graph is vertically compressed and k = -7, so the graph is translated down 7 units

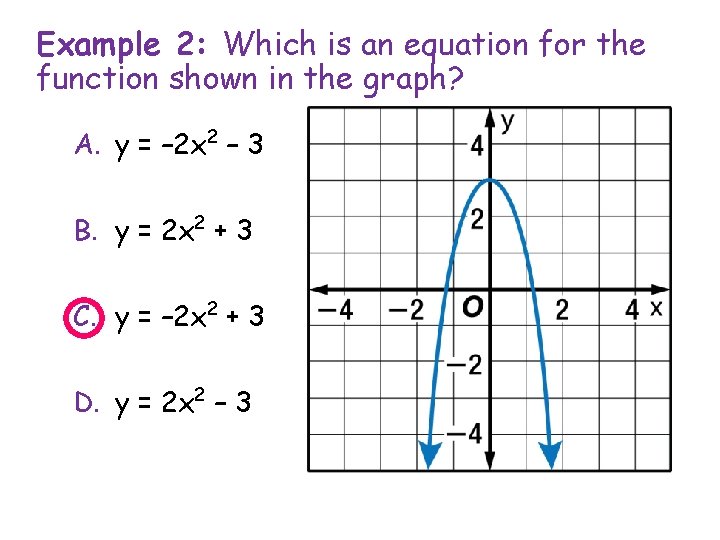
Example 2: Which is an equation for the function shown in the graph? A. y = – 2 x 2 – 3 B. y = 2 x 2 + 3 C. y = – 2 x 2 + 3 D. y = 2 x 2 – 3

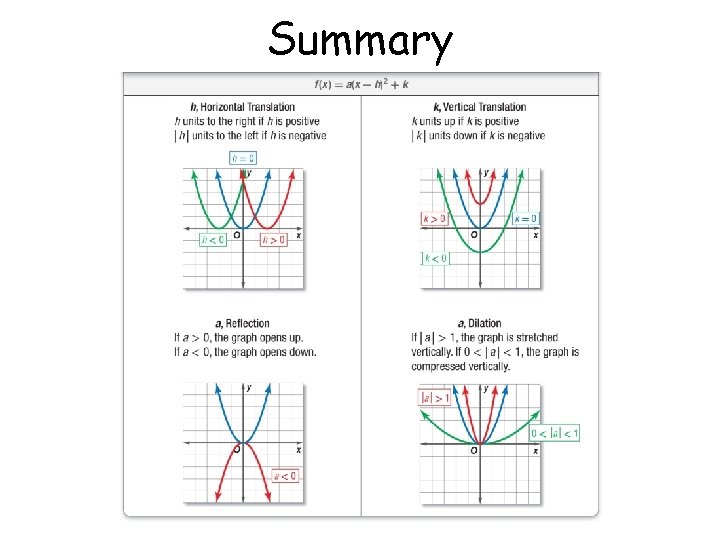
Summary