Quadratic Functions ALGEBRA 1 LESSON 8 3 Graph

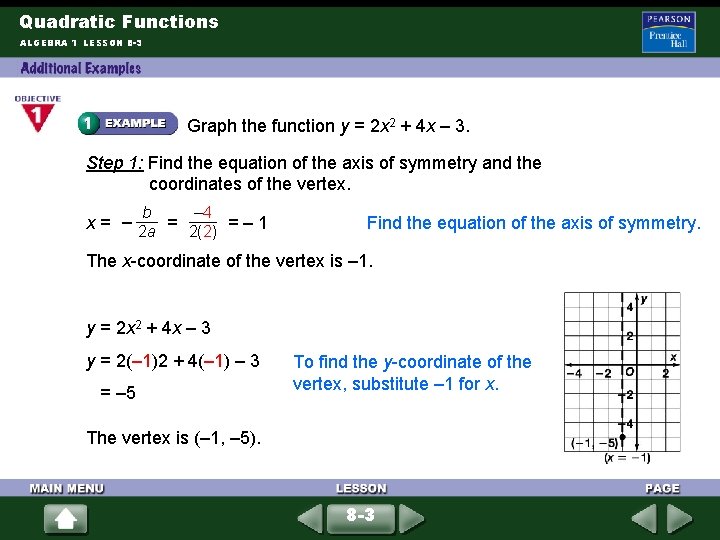
Quadratic Functions ALGEBRA 1 LESSON 8 -3 Graph the function y = 2 x 2 + 4 x – 3. Step 1: Find the equation of the axis of symmetry and the coordinates of the vertex. b – 4 x = – 2 a = 2(2) = – 1 Find the equation of the axis of symmetry. The x-coordinate of the vertex is – 1. y = 2 x 2 + 4 x – 3 y = 2(– 1)2 + 4(– 1) – 3 = – 5 To find the y-coordinate of the vertex, substitute – 1 for x. The vertex is (– 1, – 5). 8 -3

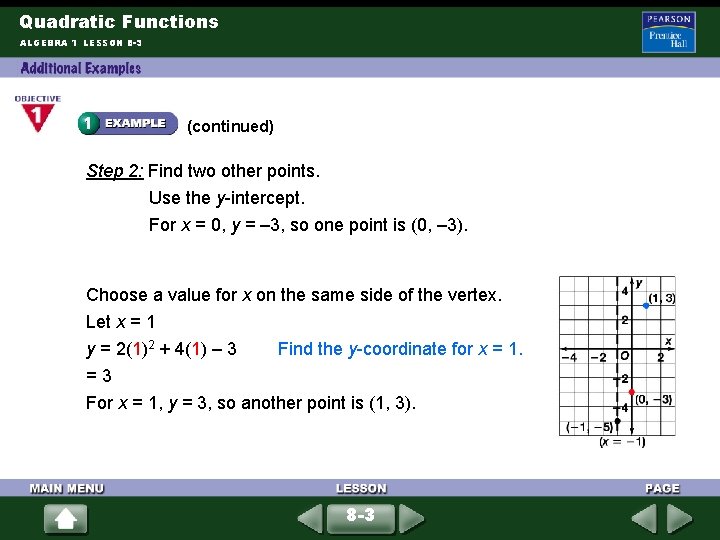
Quadratic Functions ALGEBRA 1 LESSON 8 -3 (continued) Step 2: Find two other points. Use the y-intercept. For x = 0, y = – 3, so one point is (0, – 3). Choose a value for x on the same side of the vertex. Let x = 1 y = 2(1)2 + 4(1) – 3 Find the y-coordinate for x = 1. = 3 For x = 1, y = 3, so another point is (1, 3). 8 -3

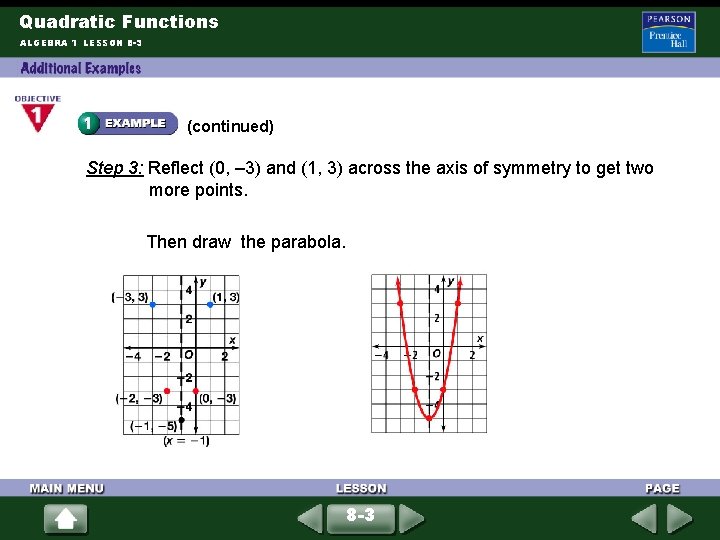
Quadratic Functions ALGEBRA 1 LESSON 8 -3 (continued) Step 3: Reflect (0, – 3) and (1, 3) across the axis of symmetry to get two more points. Then draw the parabola. 8 -3

Quadratic Functions ALGEBRA 1 LESSON 8 -3 Aerial fireworks carry “stars, ” which are made of a sparklerlike material, upward, ignite them, and project them into the air in fireworks displays. Suppose a particular star is projected from an aerial firework at a starting height of 610 ft with an initial upward velocity of 88 ft/s. How long will it take for the star to reach its maximum height? How far above the ground will it be? The equation h = – 16 t 2 + 88 t + 610 gives the height of the star h in feet at time t in seconds. Since the coefficient of t 2 is negative, the curve opens downward, and the vertex is the maximum point. 8 -3

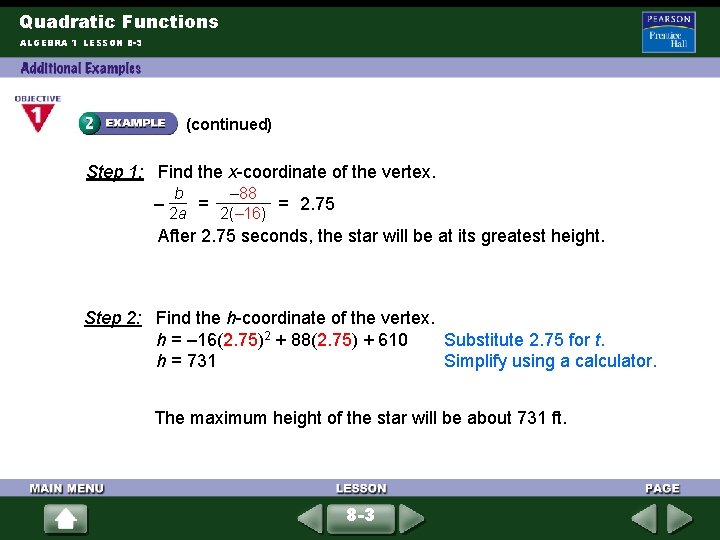
Quadratic Functions ALGEBRA 1 LESSON 8 -3 (continued) Step 1: Find the x-coordinate of the vertex. b – 88 – 2 a = 2(– 16) = 2. 75 After 2. 75 seconds, the star will be at its greatest height. Step 2: Find the h-coordinate of the vertex. h = – 16(2. 75)2 + 88(2. 75) + 610 Substitute 2. 75 for t. h = 731 Simplify using a calculator. The maximum height of the star will be about 731 ft. 8 -3

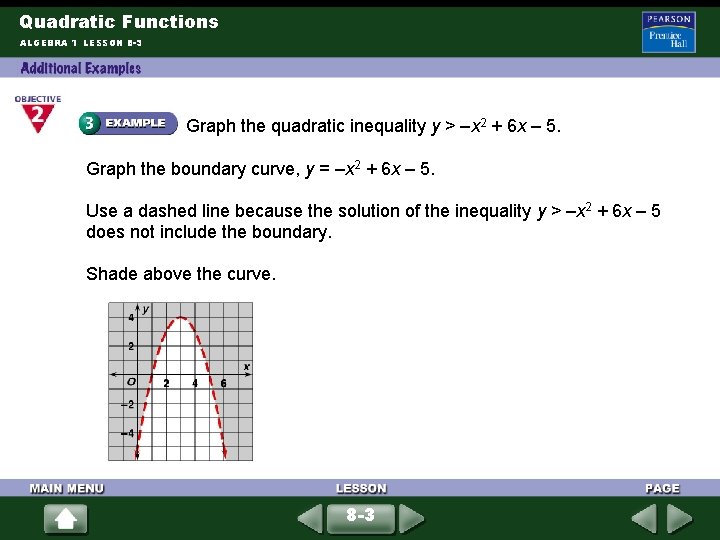
Quadratic Functions ALGEBRA 1 LESSON 8 -3 Graph the quadratic inequality y > –x 2 + 6 x – 5. Graph the boundary curve, y = –x 2 + 6 x – 5. Use a dashed line because the solution of the inequality y > –x 2 + 6 x – 5 does not include the boundary. Shade above the curve. 8 -3

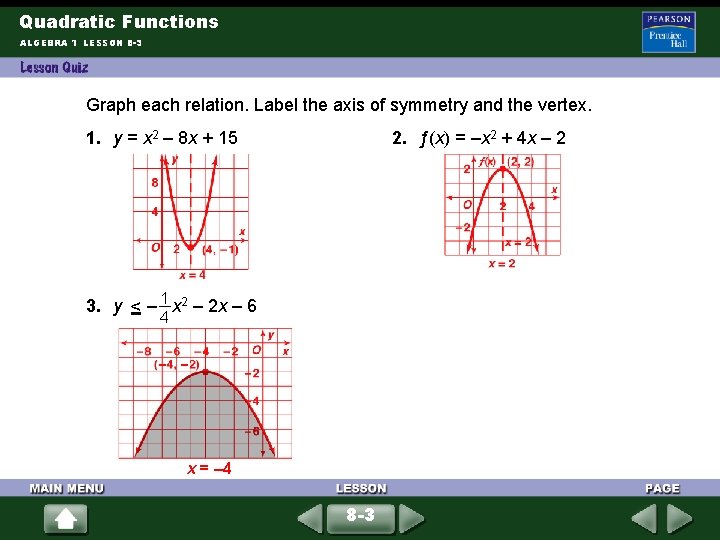
Quadratic Functions ALGEBRA 1 LESSON 8 -3 Graph each relation. Label the axis of symmetry and the vertex. 1. y = x 2 – 8 x + 15 2. ƒ(x) = –x 2 + 4 x – 2 3. y – x < 1 2 – 2 x – 6 4 x = – 4 8 -3