9 4 Transforming Quadratic Functions Objective Graph and

9 -4 Transforming Quadratic Functions Objective Graph and transform quadratic functions. Holt Algebra 1

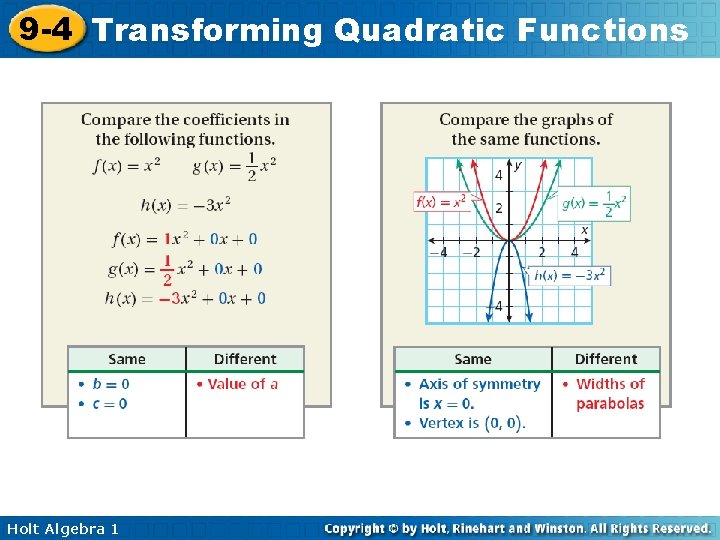
9 -4 Transforming Quadratic Functions The quadratic parent function is f(x) = x 2. The graph of all other quadratic functions are transformations of the graph of f(x) = x 2. For the parent function f(x) = x 2: • The axis of symmetry is x = 0, or the y-axis. • The vertex is (0, 0) • The function has only one zero, 0. Holt Algebra 1

9 -4 Transforming Quadratic Functions Holt Algebra 1

9 -4 Transforming Quadratic Functions Example 1 B: Comparing Widths of Parabolas Order the functions from narrowest graph to widest. f(x) = x 2, g(x) = x 2, h(x) = – 2 x 2 Step 1 Find |a| for each function. |1| = 1 |– 2| = 2 Step 2 Order the functions. h(x) = – 2 x 2 f(x) = x 2 g(x) = Holt Algebra 1 x 2 The function with the narrowest graph has the greatest |a|.

9 -4 Transforming Quadratic Functions Example 1 B Continued Order the functions from narrowest graph to widest. f(x) = x 2, g(x) = x 2, h(x) = – 2 x 2 Check Use a graphing calculator to compare the graphs. h(x) = – 2 x 2 has the narrowest graph and g(x) = x 2 has the widest graph. Holt Algebra 1

9 -4 Transforming Quadratic Functions Check It Out! Example 1 b Order the functions from narrowest graph to widest. f(x) = – 4 x 2, g(x) = 6 x 2, h(x) = 0. 2 x 2 Step 1 Find |a| for each function. |– 4| = 4 |6| = 6 |0. 2| = 0. 2 Step 2 Order the functions. g(x) = 6 x 2 f(x) = – 4 x 2 h(x) = 0. 2 x 2 Holt Algebra 1 The function with the narrowest graph has the greatest |a|.

9 -4 Transforming Quadratic Functions Check It Out! Example 1 b Continued Order the functions from narrowest graph to widest. f(x) = – 4 x 2, g(x) = 6 x 2, h(x) = 0. 2 x 2 Check Use a graphing calculator to compare the graphs. g(x) = 6 x 2 has the narrowest graph and h(x) = 0. 2 x 2 has the widest graph. Holt Algebra 1

9 -4 Transforming Quadratic Functions Holt Algebra 1

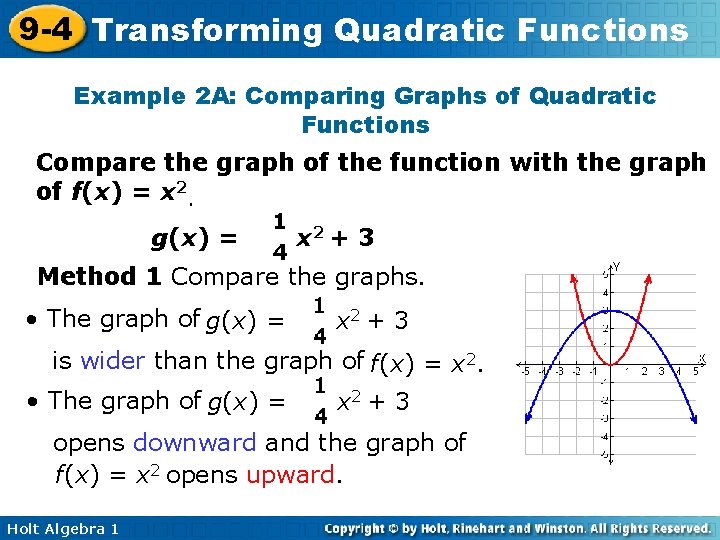
9 -4 Transforming Quadratic Functions Example 2 A: Comparing Graphs of Quadratic Functions Compare the graph of the function with the graph of f(x) = x 2. g(x) = x 2 + 3 Method 1 Compare the graphs. • The graph of g(x) = x 2 + 3 is wider than the graph of f(x) = x 2. • The graph of g(x) = x 2 + 3 opens downward and the graph of f(x) = x 2 opens upward. Holt Algebra 1

9 -4 Transforming Quadratic Functions Example 2 A Continued Compare the graph of the function with the graph of f(x) = x 2 g(x) = • x 2 + 3 The axis of symmetry is the same. • The vertex of f(x) = x 2 is (0, 0). The vertex of g(x) = x 2 + 3 is translated 3 units up to (0, 3). Holt Algebra 1

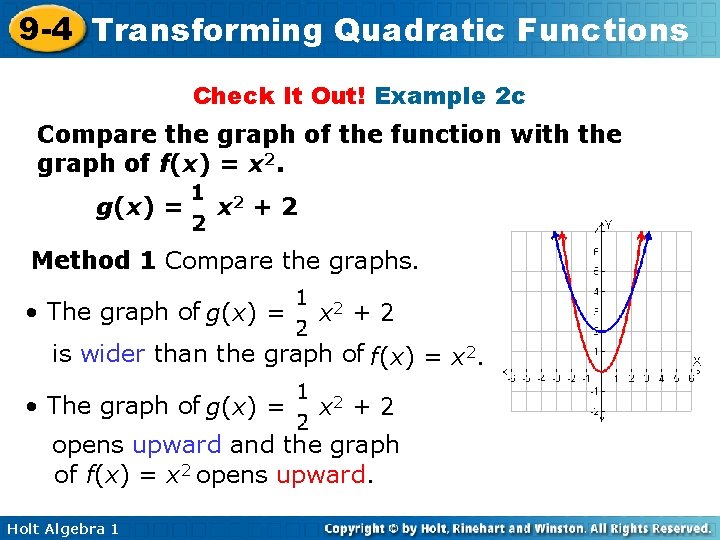
9 -4 Transforming Quadratic Functions Check It Out! Example 2 c Compare the graph of the function with the graph of f(x) = x 2. g(x) = x 2 + 2 Method 1 Compare the graphs. • The graph of g(x) = x 2 + 2 is wider than the graph of f(x) = x 2. • The graph of g(x) = x 2 + 2 opens upward and the graph of f(x) = x 2 opens upward. Holt Algebra 1

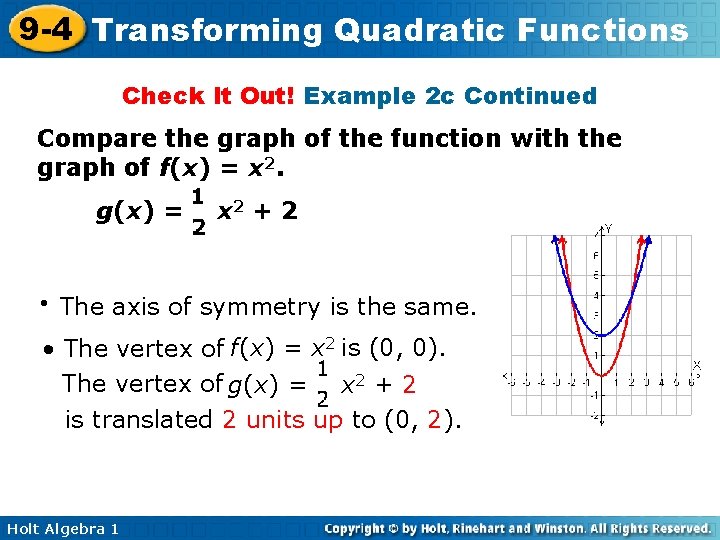
9 -4 Transforming Quadratic Functions Check It Out! Example 2 c Continued Compare the graph of the function with the graph of f(x) = x 2. g(x) = • x 2 + 2 The axis of symmetry is the same. • The vertex of f(x) = x 2 is (0, 0). The vertex of g(x) = x 2 + 2 is translated 2 units up to (0, 2). Holt Algebra 1