Quadratic Equations Quadratic Equations A basic quadratic equation

Quadratic Equations

Quadratic Equations A basic quadratic equation contains an x 2 term. Find all the possible values of x from the following: 1. x 2 = 16 x = 4 or x = - 4 2. x 2 = 81 x = 9 or x = - 9 3. x 2 + 3 = 12 x = 3 or x = -3 4. x 2 – 8 = 17 x = 5 or x = - 5 Note: Nearly all Quadratic equations have two solutions.

To solve any other quadratic equation we need to use the following principle: If Then either, Ax. B=0 A = 0 or B = 0 Example: 1. Either If Therefore x(x – 6) = 0 x = 0 or x – 6 = 0 x– 6=0 x=6 x = 6 or x = 0

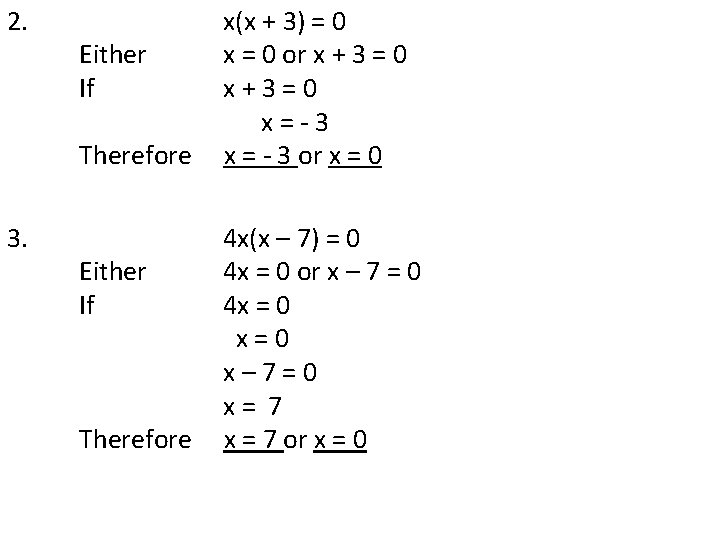
2. Either If Therefore 3. Either If Therefore x(x + 3) = 0 x = 0 or x + 3 = 0 x+3=0 x=-3 x = - 3 or x = 0 4 x(x – 7) = 0 4 x = 0 or x – 7 = 0 4 x = 0 x=0 x– 7=0 x= 7 x = 7 or x = 0

Quadratic Equations Remember: If Then either, 1. Either If or Therefore Ax. B=0 A = 0 or B = 0 (x – 2)(x + 4) = 0 x – 2 = 0 or x + 4 = 0 x– 2=0 x=2 x+4=0 x=-4 x = 2 or x = - 4

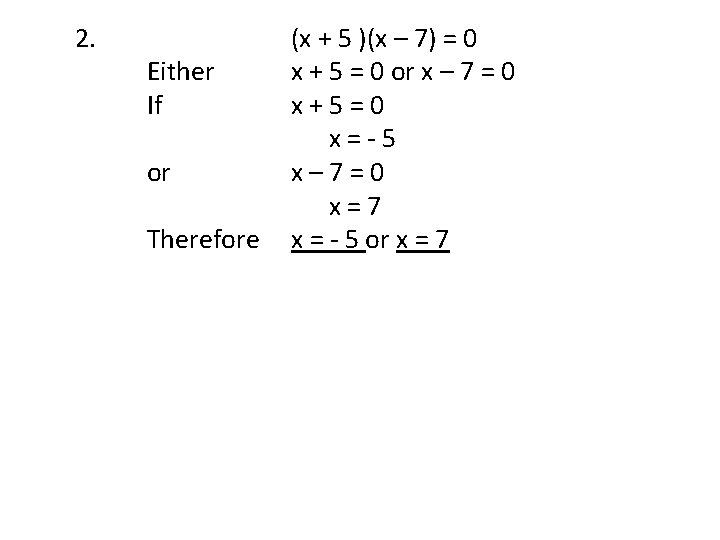
2. Either If or Therefore (x + 5 )(x – 7) = 0 x + 5 = 0 or x – 7 = 0 x+5=0 x=-5 x– 7=0 x=7 x = - 5 or x = 7

QUADRATIC EQUATIONS Most quadratic equations need to be factorised first, in order to solve them using the basic principle. Remember: x 2 – 7 x = x(x – 7) x 2 + 5 x + 6 = (x + 3)(x + 2)

Solve the following by factorisation 1. x 2 – 7 x = 0 Divide by common factor of x x(x – 7) = 0 Either x = 0 or x – 7 = 0 x=7 So x = 0 or x = 7 2. x 2 + 3 x = 0 Divide by common factor of x x(x + 3) = 0 Either x = 0 or x + 3 = 0 x=-3 So x = 0 or x = - 3

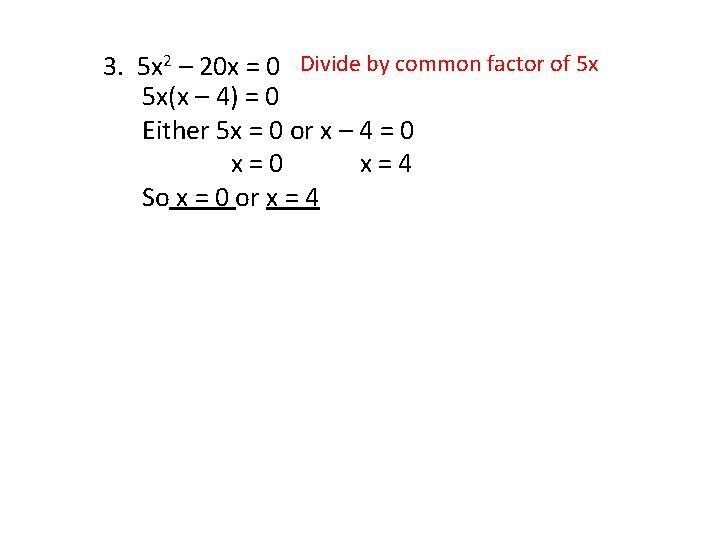
3. 5 x 2 – 20 x = 0 Divide by common factor of 5 x 5 x(x – 4) = 0 Either 5 x = 0 or x – 4 = 0 x=4 So x = 0 or x = 4

4. x 2 + 5 x + 6 = 0 Factorise into a double bracket (x + 3)(x + 2) = 0 If x + 3 = 0 or x + 2 = 0 So x=-3 x=-2 x = - 3 or x = - 2 5. x 2 – 9 x + 14 = 0 Factorise into a double bracket (x – 7)(x – 2) = 0 If x – 7 = 0 or x – 2 = 0 So x = 7 or x= 2 x = 7 or x = 2