DualUse Ballute Research Equations of Motion Part 2

Dual-Use Ballute Research Equations of Motion – Part 2 (rotating) 3/24/2006 Kristin Medlock 1

Assumptions • Atmosphere rotates with the planet • Rotating planet/ atmosphere (at constant Ω rad/sec) • Inverse-square gravity field • Spherically symmetric planet 3/24/2006 Kristin Medlock 2

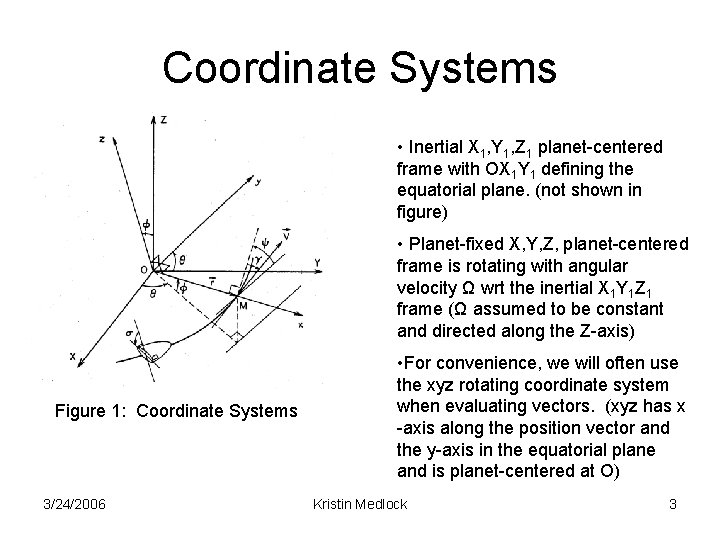
Coordinate Systems • Inertial X 1, Y 1, Z 1 planet-centered frame with OX 1 Y 1 defining the equatorial plane. (not shown in figure) • Planet-fixed X, Y, Z, planet-centered frame is rotating with angular velocity Ω wrt the inertial X 1 Y 1 Z 1 frame (Ω assumed to be constant and directed along the Z-axis) Figure 1: Coordinate Systems 3/24/2006 • For convenience, we will often use the xyz rotating coordinate system when evaluating vectors. (xyz has x -axis along the position vector and the y-axis in the equatorial plane and is planet-centered at O) Kristin Medlock 3

Newton’s 2 nd Law (X 1 Y 1 Z 1) (1) NOTE: derivatives are taken wrt inertial (X 1 Y 1 Z 1) frame In deriving the EOMs we will use the planet fixed axis as the reference frame, so Eq. (1) needs to be given as such. 3/24/2006 Kristin Medlock 4

Newton’s 2 nd Law (X 1 Y 1 Z 1 → XYZ) • Using the Basic Kinematic Equation (BKE): (2) (3) • Simplifying Eq. (3), (note: Xdω/dt=0): . 3/24/2006 (4) Kristin Medlock 5

Newton’s 2 nd Law (XYZ) • Substituting (4) into (1), we get Newton’s 2 nd Law in terms of the planet-fixed reference frame: (5) 3/24/2006 Kristin Medlock 6

Find Cross Products from Eq. (5) Looking at Fig. 1, the spacecraft’s position and velocity vectors can be expressed in the xyz-frame as follows: (6) (7) Also, the planet’s angular velocity is given by: (8) 3/24/2006 Kristin Medlock 7

Find Cross Products from Eq. (5) Using (7) & (8), we get the following cross products: (9) (10) 3/24/2006 Kristin Medlock 8

Derivative of wrt XYZ • Basic Kinematic Equation (BKE) (11) • Angular Velocity of xyz-frame wrt XYZ-frame (12) • Substitute (12) into (11) and simplify (13) . 3/24/2006 Kristin Medlock 9

Equations of Motion: • Set (13) equal to (7) and solve for (14 a) (14 b) (14 c) 3/24/2006 Kristin Medlock 10

Derivative of wrt XYZ • BKE (15) • Substitute (12) & (13) into (15) (16) 3/24/2006 Kristin Medlock 11

Derivative of • Substitute terms for wrt XYZ from (14) into (16) (17) 3/24/2006 Kristin Medlock 12

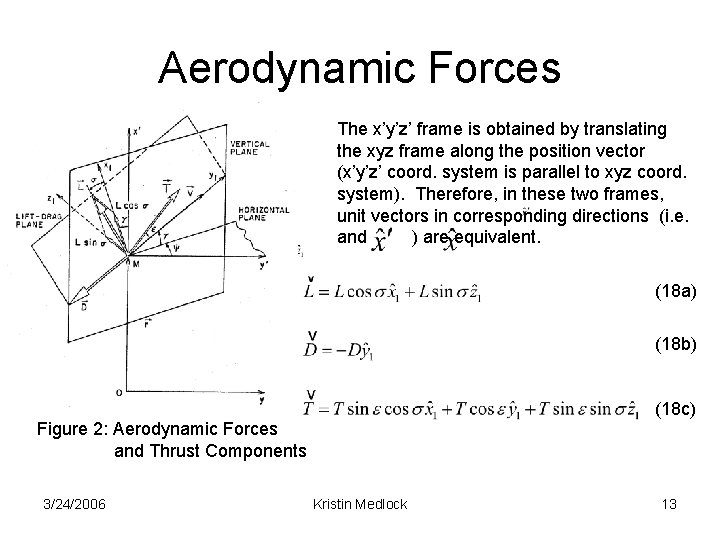
Aerodynamic Forces The x’y’z’ frame is obtained by translating the xyz frame along the position vector (x’y’z’ coord. system is parallel to xyz coord. system). Therefore, in these two frames, unit vectors in corresponding directions (i. e. and ) are equivalent. (18 a) (18 b) (18 c) Figure 2: Aerodynamic Forces and Thrust Components 3/24/2006 Kristin Medlock 13

Aerodynamic Forces • By summing the forces in each direction, we arrive at the normal, tangential, and binormal forces, respectively: (19 a) (19 b) (19 c) • So, in the x’y’z’-frame, the force vectors are: (20 a) (20 b) (20 c) 3/24/2006 Kristin Medlock 14

Gravitational Force (21) Recall: inverse-square gravity field (i. e. g is a function of r) Total Force (22) 3/24/2006 Kristin Medlock 15

Newton’s 2 nd Law (XYZ) • Recall Eq. (5) : (5) • Substitute (9), (10), (17), (20), &(21) into(5) and solve for (23 a) (23 b) (23 c) 3/24/2006 Kristin Medlock 16

Centrifugal and Coriolis Force Terms (24 a) (24 b) (24 c) (24 d) (24 e) 3/24/2006 Kristin Medlock 17

Equations of Motion: Substituting (24) into (23) the EOMs can be rewritten as: (25 a) (25 b) (25 c) 3/24/2006 Kristin Medlock 18

SUMMARY Equations 14(a-c) and 25(a-c) give the six EOMs for flight over a rotating spherical planet wrt the planet fixed reference frame (XYZ). 3/24/2006 (14 a) (25 a) (14 b) (25 b) (14 c) (25 c) Kristin Medlock 19