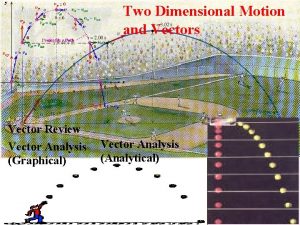
Vectors and Two Dimensional Motion Chapter 3 Constant

















- Slides: 33

Vectors and Two Dimensional Motion Chapter 3

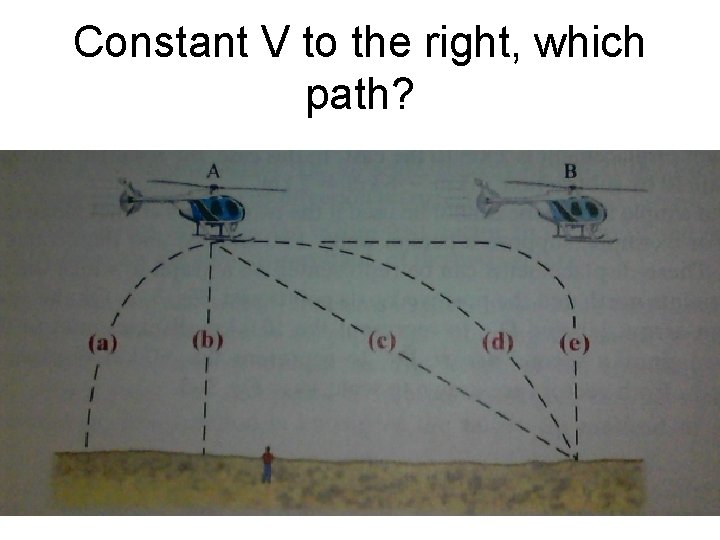
Constant V to the right, which path?

Addition of Vectors – Graphical Methods One-Dimensional Vector Addition: If two vectors are in the same direction and along the same line, the resultant vector will be the arithmetic sum of the magnitudes and the direction will be in the direction of the original vectors. + 4 = 2 + -2 6 = 5 3

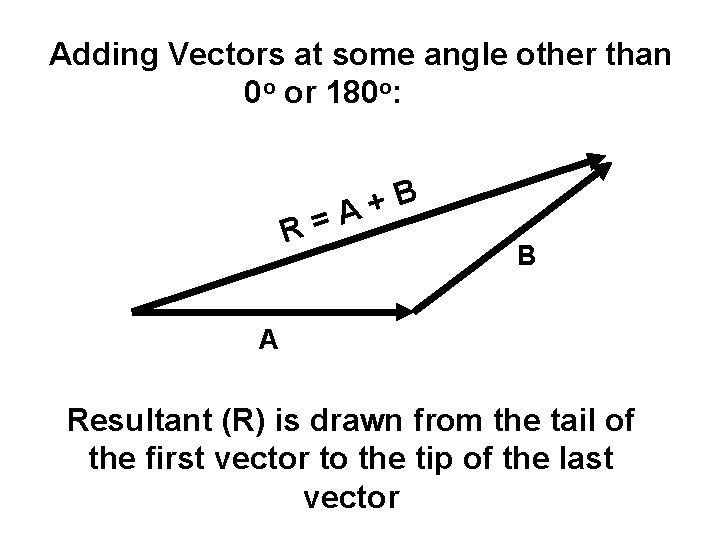
Adding Vectors at some angle other than 0 o or 180 o: R= B + A B A Resultant (R) is drawn from the tail of the first vector to the tip of the last vector

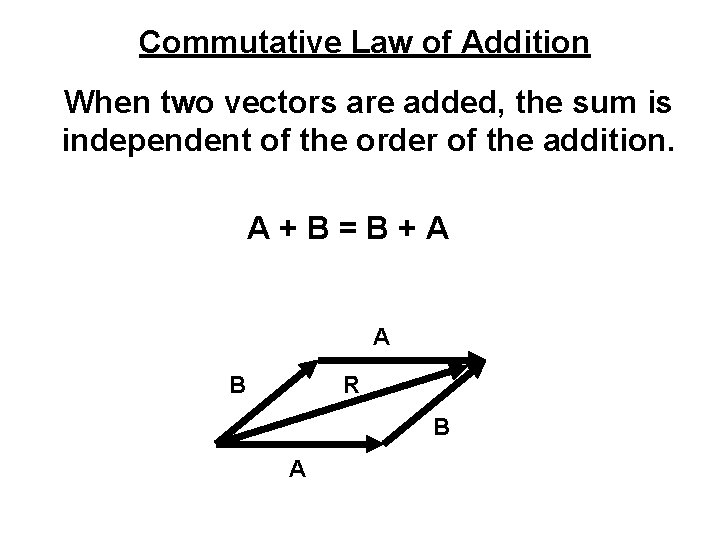
Commutative Law of Addition When two vectors are added, the sum is independent of the order of the addition. A+B=B+A A B R B A


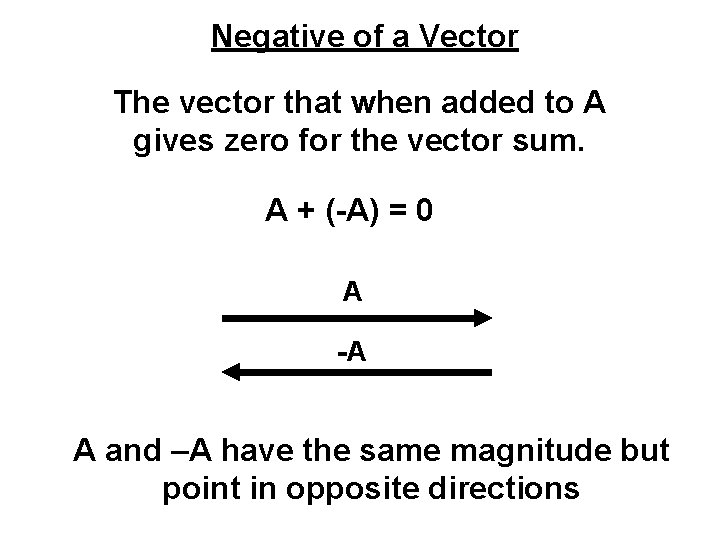
Negative of a Vector The vector that when added to A gives zero for the vector sum. A + (-A) = 0 A -A A and –A have the same magnitude but point in opposite directions

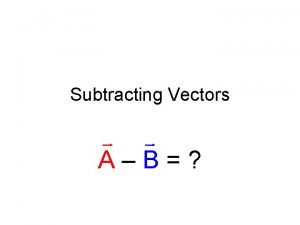
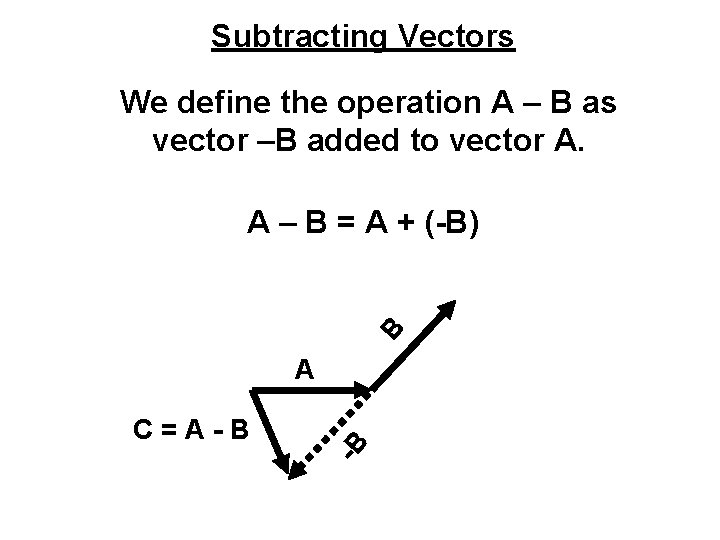
Subtracting Vectors We define the operation A – B as vector –B added to vector A. B A – B = A + (-B) C=A-B -B A

Multiplying a Vector by a Scalar When vector A is multiplied by a positive scalar quantity m, then the product m. A is a vector with the same direction of A and magnitude m. A. When vector A is multiplied by a negative scalar quantity -m, then the product -m. A is a vector directed opposite A and magnitude m. A.

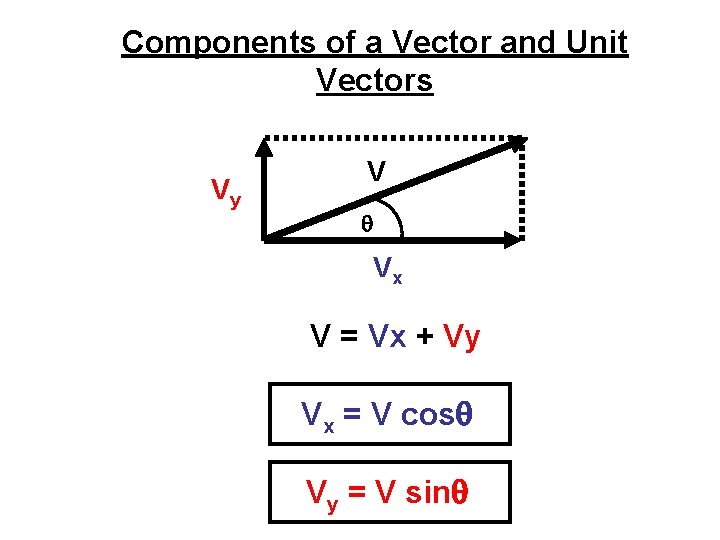
Components of a Vector and Unit Vectors Vy V Vx V = Vx + Vy Vx = V cos Vy = V sin

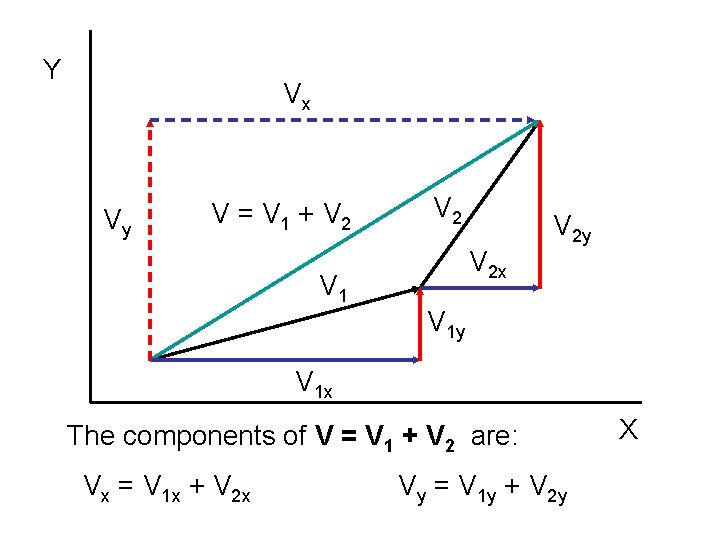
Y Vx Vy V = V 1 + V 2 V 1 V 2 x V 2 y V 1 x The components of V = V 1 + V 2 are: Vx = V 1 x + V 2 x Vy = V 1 y + V 2 y X

Two ways to specify a vector: 1. We can give its components, Vx and Vy 2. We can give its magnitude V and the angle it makes with the positive x axis. V V 2 = V x 2 + V y 2 tan = Vy / Vx Vsinθ = Vy θ Vcosθ = Vx

Analytically adding Vectors • Resolve each vector into its x and y components using sin and cos functions. V 1 x = V 1 cos V 1 y = V 1 sin • Add the x components together and get the x component of the resultant Add the y component together to get the y component of the resultant. Vx = V 1 x + V 2 x Vy = V 1 y + V 2 y

• Find the magnitude and direction using the following: V 2 = V x 2 + V y 2 tan = Vy / Vx

RELATIVE VELOCITY • When measuring the position or velocity, you must first define your frame of reference. – e. g. For a viewer on a ship or on the land. For one, the frame of reference is the ship, for the other, it is the land.

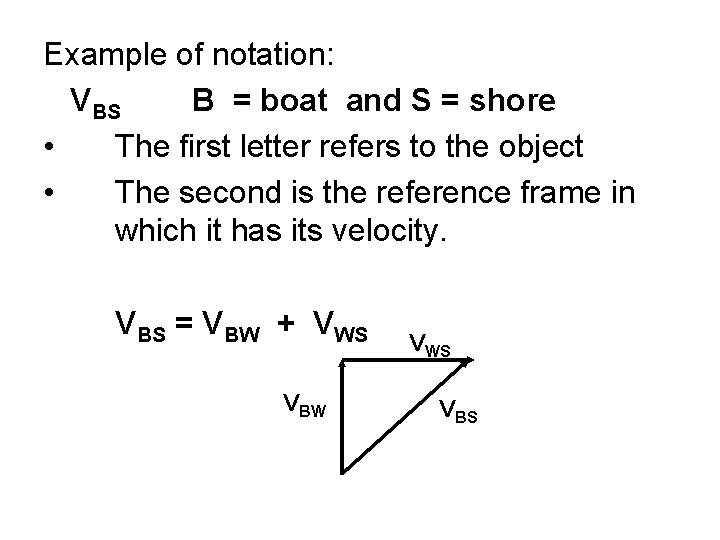
Example of notation: VBS B = boat and S = shore • The first letter refers to the object • The second is the reference frame in which it has its velocity. VBS = VBW + VWS VBW VWS VBS

Done

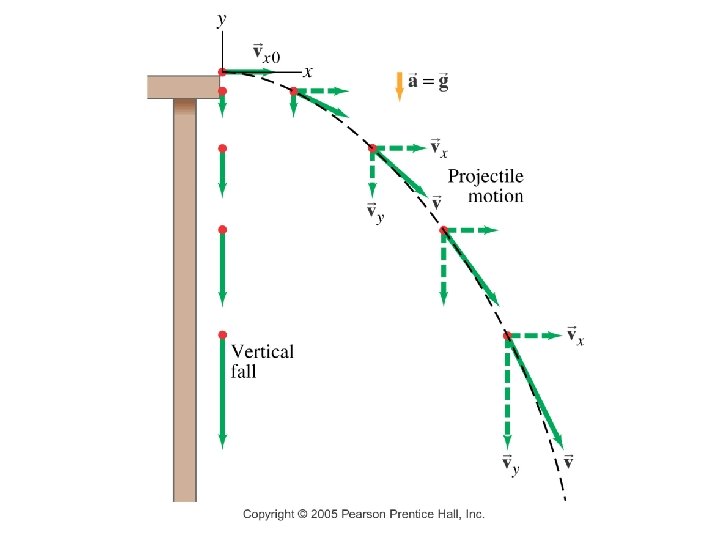
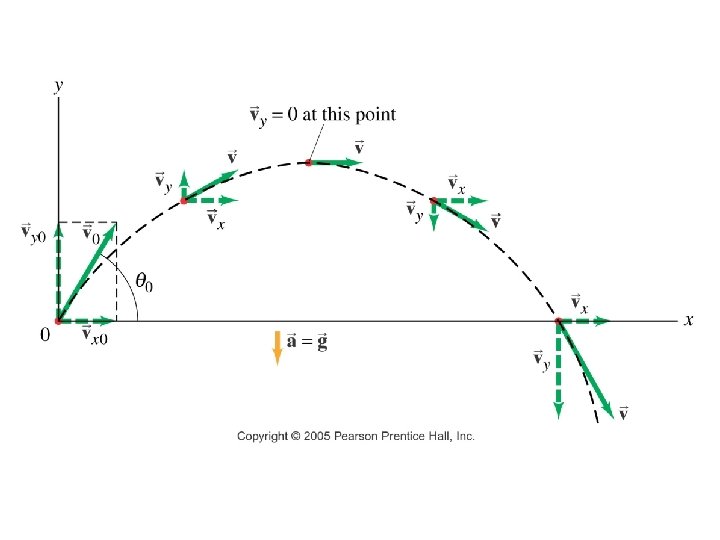
Projectile Motion • Projectiles: Motion of objects given an initial velocity that then moves only under the force of gravity • Trajectory: The path a projectile follows • Motion of a projectile: Described in terms of its position, velocity, and acceleration.



Horizontal Motion Equations vx = vxo Vertical Motion Equations vy = vyo + gt y – yo = vyot + 1/2 gt 2 x = xo + vxot vy 2 = vyo 2 + 2 g(y - yo) Define initial direction of motion as positive.

Example 3 A ball rolls off a table 1. 0 m high with a speed of 4 m/s. How far from the base of the table does it land ?

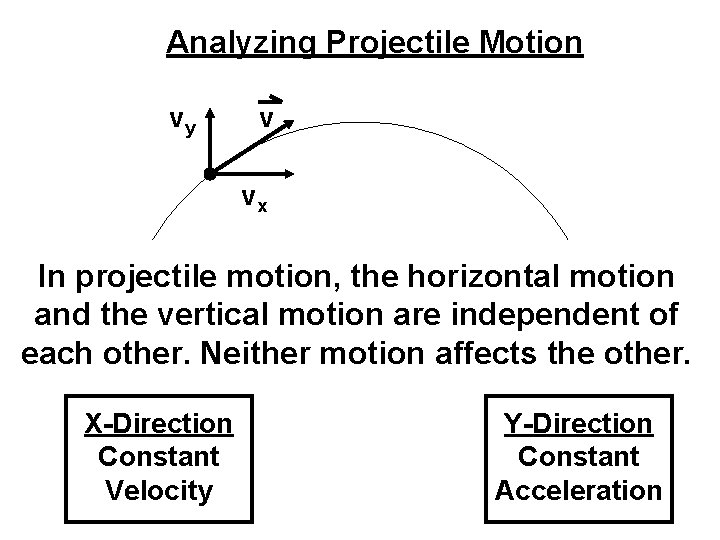
Analyzing Projectile Motion vy v vx In projectile motion, the horizontal motion and the vertical motion are independent of each other. Neither motion affects the other. X-Direction Constant Velocity Y-Direction Constant Acceleration


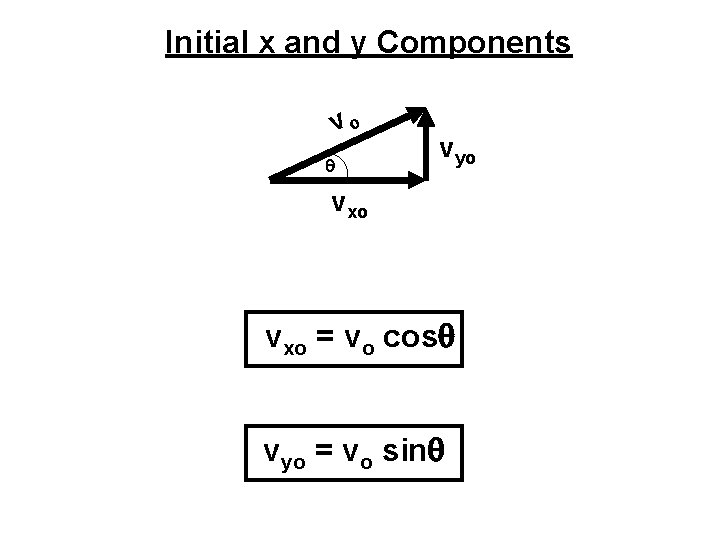
Initial x and y Components vo vyo vxo = vo cos vyo = vo sin

Horizontal Motion Equations vx = vxo Vertical Motion Equations vy = vyo + gt y – yo = vyot + 1/2 gt 2 x = xo + vxot vy 2 = vyo 2 + 2 g(y - yo) Define initial direction of motion as positive.

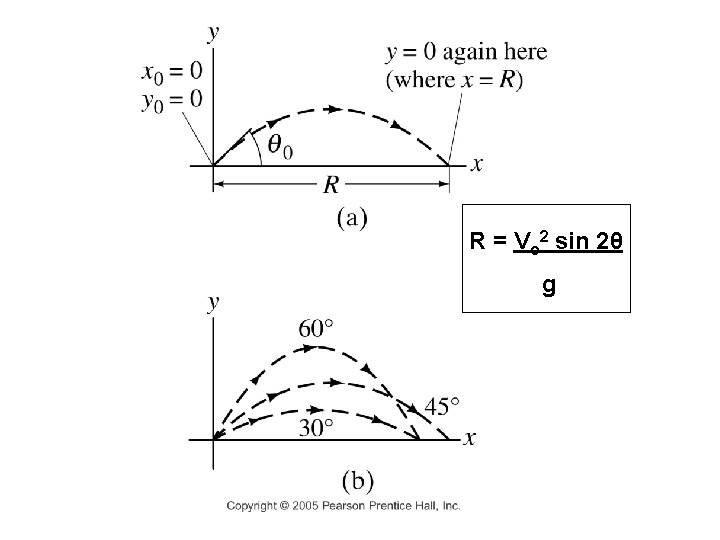
R = Vo 2 sin 2θ g

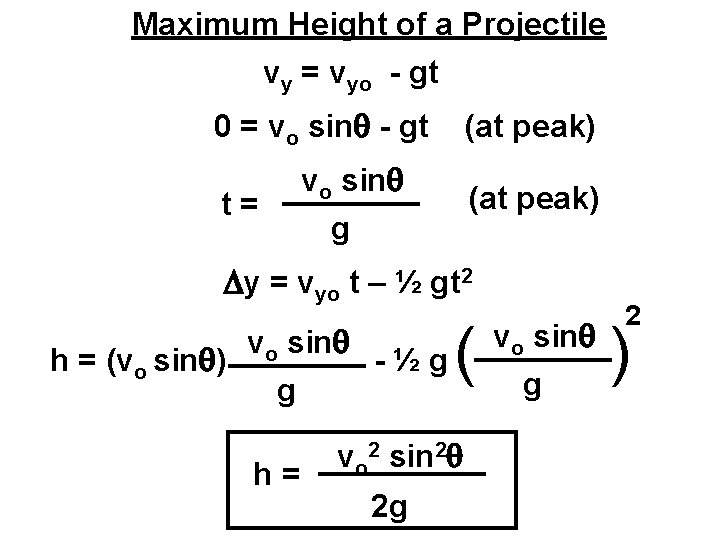
Maximum Height of a Projectile vy = vyo - gt 0 = vo sin - gt (at peak) vo sin t= (at peak) g Dy = vyo t – ½ gt 2 h = (vo sin ) vo sin g h= -½g ( vo 2 sin 2 2 g vo sin g 2 )

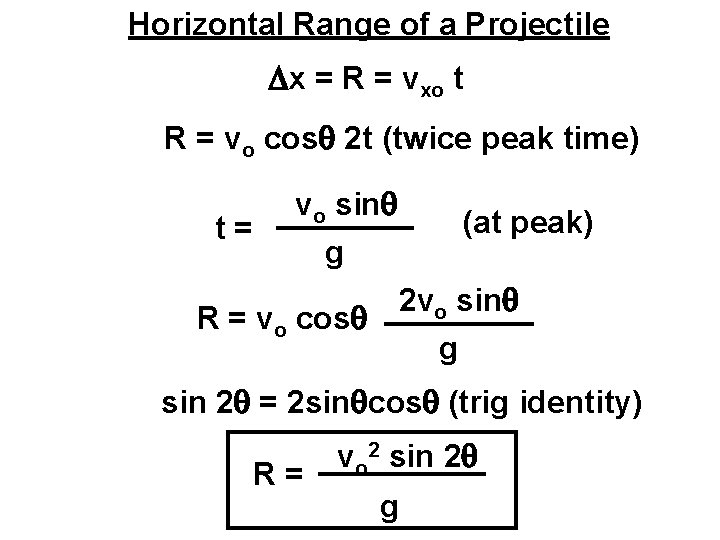
Horizontal Range of a Projectile Dx = R = vxo t R = vo cos 2 t (twice peak time) t= vo sin g (at peak) 2 vo sin R = vo cos g sin 2 = 2 sin cos (trig identity) R= vo 2 sin 2 g

Example 4 An arrow is shot from a castle wall 10. m high. It leaves the bow with a speed of 40. m/s directed 37 o above the horizontal. a) Find the initial velocity components. b) Find the maximum height of the arrow. c) Where does the arrow land ? d) How fast is the arrow moving just before impact ?

Example 5 A stone is thrown from the top of a building upward at an angle of 30 o to the horizontal with an initial speed of 20. 0 m/s. a) If the building is 45. 0 m high, how long does it take the stone to reach the ground ? b) What is the speed of the stone just before it strikes the ground ?

Example 6 : 1985 #1 A projectile is launched from the top of a cliff above level ground. At launch the projectile is 35 m above the base of the cliff and has a velocity of 50 m/s at an angle of 37 o with the horizontal. Air resistance is negligible. Consider the following two cases and use g = 10 m/s 2, sin 37 o = 0. 60, and cos 37 o = 0. 80. Case I : The projectile follows the path shown by the curved line in the following diagram. a) Calculate the total time from launch until the projectile hits the ground at point C. b) Calculate the horizontal distance R that the projectile travels before it hits the ground. c) Calculate the speed of the projectile at points A, B, and C.

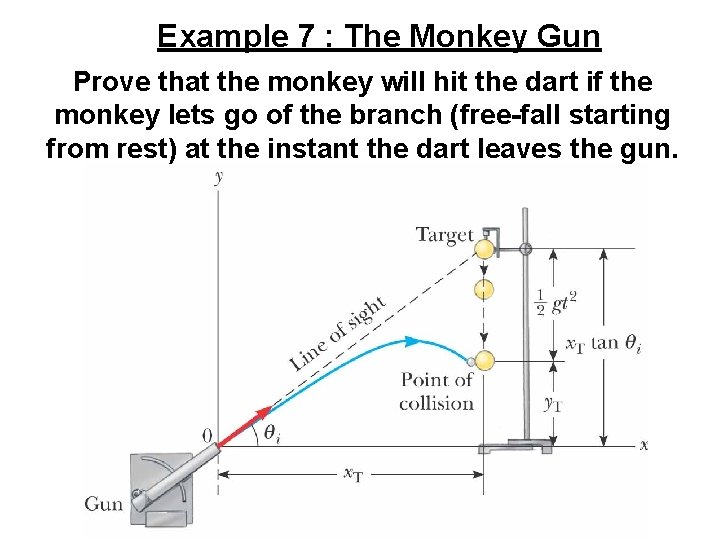
Example 7 : The Monkey Gun Prove that the monkey will hit the dart if the monkey lets go of the branch (free-fall starting from rest) at the instant the dart leaves the gun.
 Two dimensional motion examples
Two dimensional motion examples Circular motion is one dimensional or two dimensional
Circular motion is one dimensional or two dimensional Two dimensional motion
Two dimensional motion Two dimensional motion definition
Two dimensional motion definition Constant pointer and pointer to constant
Constant pointer and pointer to constant üyou
üyou 9 pointers
9 pointers Equilibrium occurs when
Equilibrium occurs when Constant to pointer in c
Constant to pointer in c Display the address of intval using cout and intptr.
Display the address of intval using cout and intptr. Filtration formula
Filtration formula Gas constants
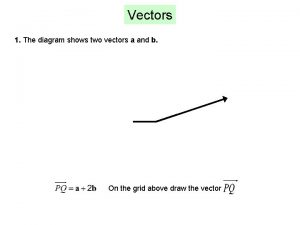
Gas constants Each part of the diagram shows two vectors, a and b.
Each part of the diagram shows two vectors, a and b. The diagram shows two vectors that point west and north.
The diagram shows two vectors that point west and north. Collinear vector
Collinear vector A student adds two vectors with magnitudes of 200 and 40
A student adds two vectors with magnitudes of 200 and 40 Chapter 2 section 1 describing motion answer key
Chapter 2 section 1 describing motion answer key Chapter 2 motion section 1 describing motion answer key
Chapter 2 motion section 1 describing motion answer key Section 1 describing motion worksheet answer key
Section 1 describing motion worksheet answer key Metals tend to be
Metals tend to be Rate constant vs equilibrium constant
Rate constant vs equilibrium constant Complex ion formation and solubility
Complex ion formation and solubility Is ag an ion
Is ag an ion Characteristics of two dimensional shapes
Characteristics of two dimensional shapes Two-dimensional structure composed of rows and columns
Two-dimensional structure composed of rows and columns Two-dimensional structure composed of rows and columns
Two-dimensional structure composed of rows and columns Find the resultant of two like parallel forces
Find the resultant of two like parallel forces Inner product of two vectors
Inner product of two vectors Vectors in one dimension
Vectors in one dimension How do you add vectors algebraically
How do you add vectors algebraically Dot product of two vectors
Dot product of two vectors Vectors parallel
Vectors parallel Cross product of two vectors
Cross product of two vectors Adding two vectors
Adding two vectors