Topic EQUATIONS Simple Equations Fractional Equations Guidelines Equations

Topic: EQUATIONS Simple Equations Fractional Equations

Guidelines • Equations must be balanced. You must respect the laws of equations. • The goals is to bring variable on the left and number to the right. • Coefficient (or number) of variable +1. For example, 1 x = 5; just put x = 5

Examples 1. #1) Solve: x = 5 + 2 x=7 2. x = 5 (2 + 7) – ( 7 – 3) x = 10 + 35 – 7 + 3 • Remember a minus before a bracket changes the sign of everything in the bracket x = 41

Guidelines con’t • Whatever you do to one side, you must do to another. If you add 5 to one side, you must add 5 to the other side. • If you have a number near the variable, always divide it by that number. For example 2 x = 10; divide both by 2. x = 5 • If -5 x = 10; divide by -5; x = -2 • When it changes signs, it changes signs

Example • 4 x + 1 = 13 4 x = 13 - 1 (the 1 changed sides so it changes signs) 4 x = 12 (divide both sides by 4) x=3

Verification • If you want to guarantee that you have the right answer you should verify. To verify: replace the number into the letter in the question. • 4 x + 1 = 13 (Original question) & x=3 4 (3) + 1 = 13 12+1=13 13=13 This is true; you have the right answer.

Guideline & Example • • 3 x – 5 = 10 x + 10 -3 x - 10 x = 10 + 5 -13 x = 15 x = -1. 15

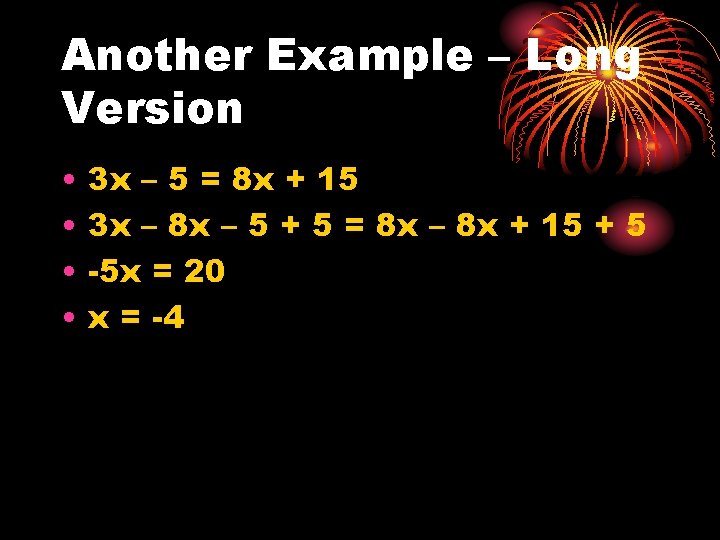
Another Example – Long Version • • 3 x – 5 = 8 x + 15 3 x – 8 x – 5 + 5 = 8 x – 8 x + 15 + 5 -5 x = 20 x = -4

Same example – Short Version • • 3 x – 5 = 8 x + 15 -5 x = 20 x = -4 We will continue with the short version ; )

More examples • • 4 x + 7 = 2 x – 11 2 x = -18 x=-9 Verify! 4 (-9) + 7 = 2 (-9) – 11 -36 + 7 = -18 – 11 - 29 = -29 (You have the right answer)

Another Example • 9 x – 5 = 2 x + 4 7 x = 9 x = 1. 29 You can still verify this! 9 (1. 29) – 5 = 2 (1. 29) + 4 6. 61 = 6. 58 (rounding error… close enough!)

More Examples • 3 x + 5 = 6 x + 25 • x = - 6. 67 • 4 x + 2 = 8 x – 31 • X = 8. 25 --- are you verifying? )

Reminders • Distributive property • 5(3 x + 2) means you multiply 5 by everything in the bracket • 15 x + 10 • A minus sign before the bracket changes the sign of everything in the bracket

Now to add some fun – and have them longer • 3 (5 x-7) – (2 x+8) = 2 (3 x-1) • 15 x – 21 – 2 x – 8 = 6 x – 2 • CLEAN IT UP BEFORE MOVING NUMBERS OR LETTERS • 13 x – 29 = 6 x – 2 • 7 x = 27 • x = 3. 86 • Verify!

Verify • 3 (5 x-7) – (2 x+8) = 2 (3 x-1) • 3 (5(3. 86) – 7) – (2(3. 86) - 8 = 2 (3(3. 86) – 1) • 3 (12. 3) – 7. 72 – 8 = 2 (10. 58) • 21. 18 = 21. 16 (rounding error – close enough!)

Quiz # 3 Equations • 1) • 2) • 3) • 4) • 5) 5 x 2 x 9 x 3 x 6 x – – – 7 5 2 7 1 = = = 3 x + 7 4 x + 7 - 40 + 5 x 8 x + 20

Quiz #3 Equation Solutions • • • 1) 7 (1 a) 2) – 6 (1 b) 3) -9. 5 (1 i) 4) – 5. 4 (1 o) 5) -10. 5 6) -1 (1 u) 7) 2 (1 w) 8) –x – 1 (minus before a bracket!) 9) 2 x + 5 (don’t mix apples & oranges!) 10) – 10

Fractional Equations • Once again we want to get rid of the fraction • Find the LCD (Lowest Common Denominator) • Multiply every term to get the LCD.

Example 1. x – 2 = 11 5 3 15 LCD of 5, 3 and 15 is LCD is 15 3 x – 10 = 11 3 x = 21 X = 7 and then yes… VERIFY

Verify 1. x – 2 = 11 5 3 15 7/5 – 2/3 = 11 / 15 0. 73 = 0. 73 it works!

Another example • 2 x – 11 = 3 x – 5 7 14 28 7 8 x – 22 = 3 x – 20 5 x = 2 x = 0. 4

Another Example • 3 – 11 x = 5 + 5 x 8 12 24 6 9 – 22 x = 5 + 20 x -42 x = -4 X = 0. 1

Final Example (Hard) • 3 x – 2 – 11 x + 8 x = 3 – 7 x + 1 5 3 30 15 2 15 30 18 x – 20 – 11 x + 16 x = 45 – 14 x +1 37 x = 66 X = 1. 78