Mr Smith DHS 1617 Simple Harmonic Motion SHM

Mr Smith DHS 16/17 Simple Harmonic Motion (SHM)

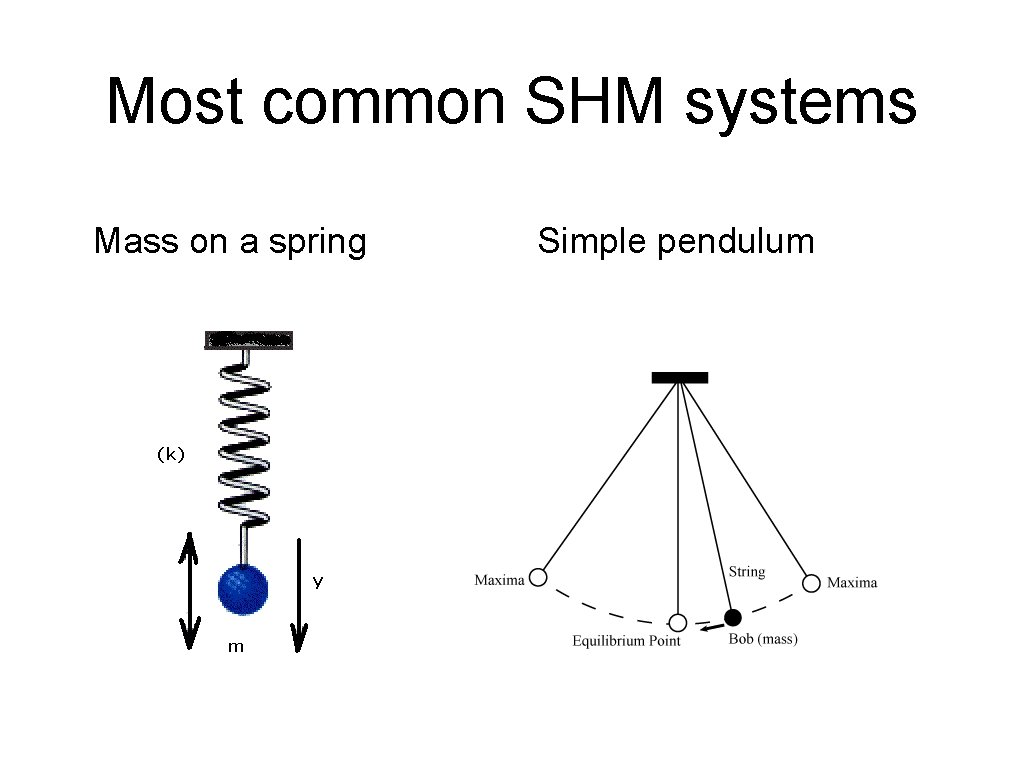
Most common SHM systems Mass on a spring Simple pendulum

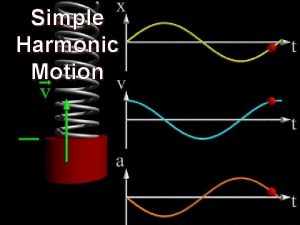
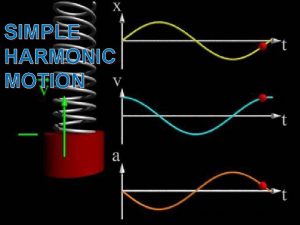
Displacement-time

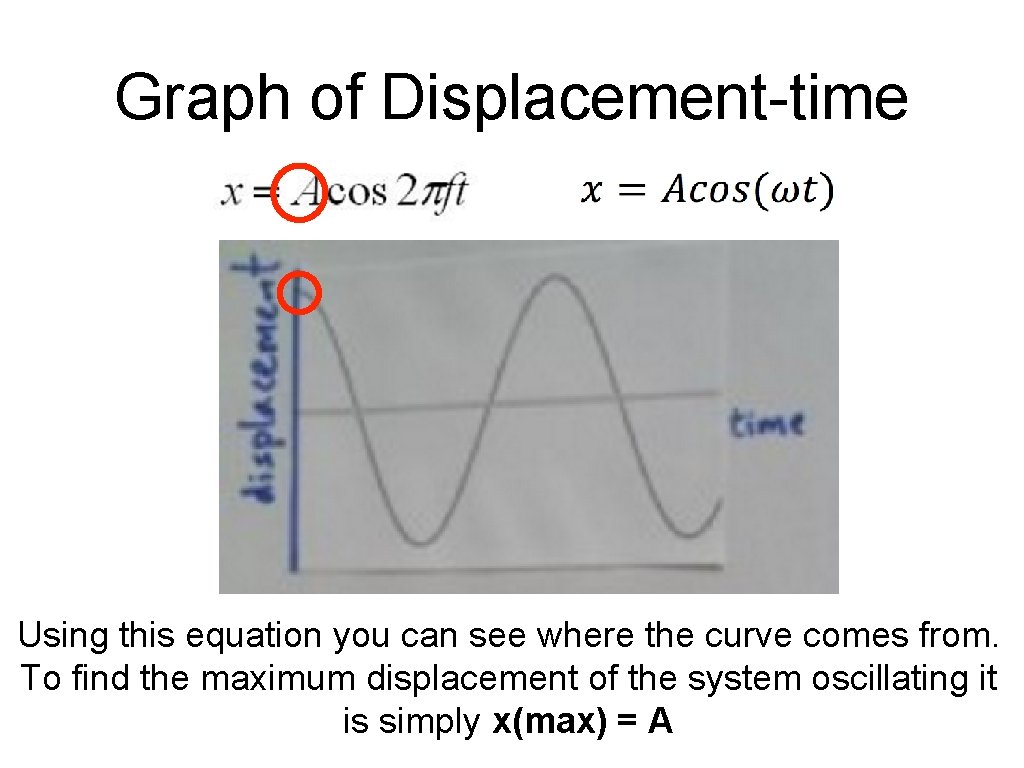
Graph of Displacement-time Using this equation you can see where the curve comes from. To find the maximum displacement of the system oscillating it is simply x(max) = A

Velocity-time The velocity-time graph is simply the gradient of the displacement-time graph! If you differentiate (because it’s a curve) x with respect to time you get…

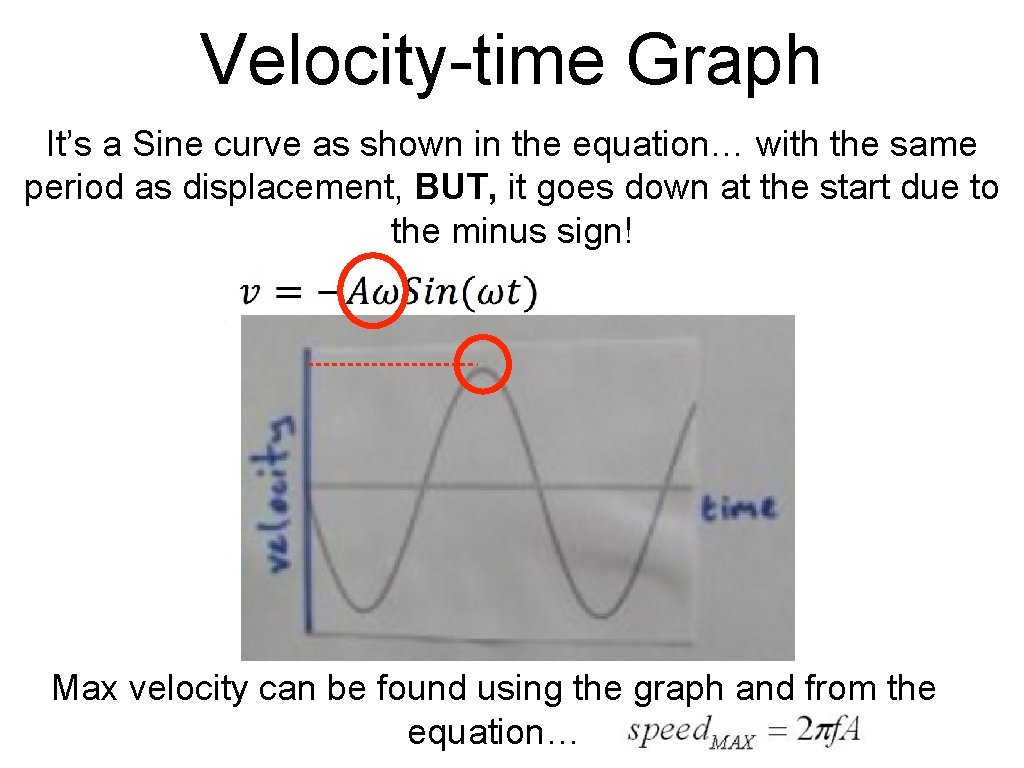
Velocity-time Graph It’s a Sine curve as shown in the equation… with the same period as displacement, BUT, it goes down at the start due to the minus sign! Max velocity can be found using the graph and from the equation…

Acceleration-time Again… Differentiate the velocity equation w. r. t time and we get… Look back at displacement…. We can substitute this equation into acceleration and we get… The SHM equation!!!!

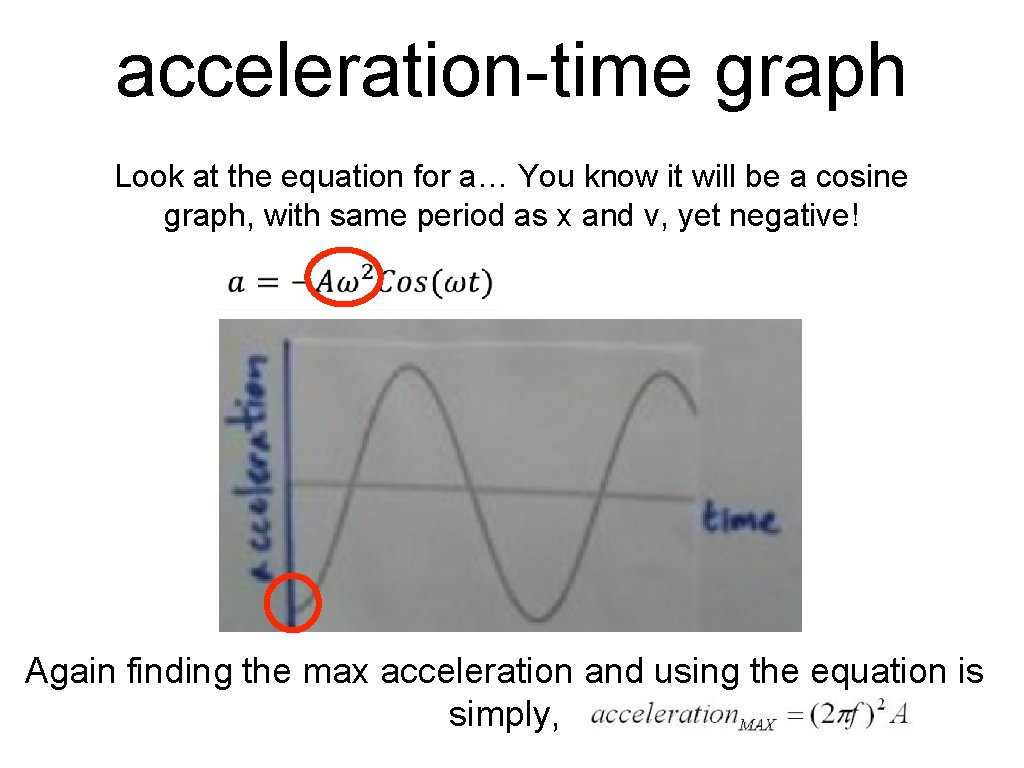
acceleration-time graph Look at the equation for a… You know it will be a cosine graph, with same period as x and v, yet negative! Again finding the max acceleration and using the equation is simply,

Maximum x, v & a Maximum displacement is simply… displacementmax = A

To Summarise… Systems that oscillate can be said to be undergoing Simple Harmonic Motion (SHM) if, and only if, the following points are true! Which can be written as the equation… We can also map the displacement, velocity and acceleration of the oscillating systems using the equations mentioned in this powerpoint. Accompanying graphs can be drawn and maximum amplitudes of x, v and a can be found!

Equations for this topic 6. 1. 2 SHM Do not forget this equation!!

Go to the link on the website to practice questions on SHM 6. 1. 2 As always… Any problems, come see me!!