Simple Harmonic Motion Simple harmonic motion Motion consisting

Simple Harmonic Motion

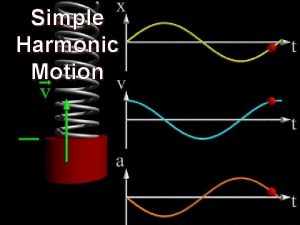
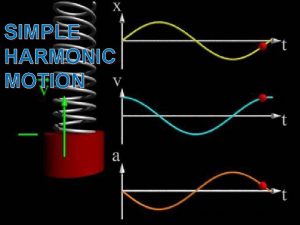
Simple harmonic motion Motion consisting of regular, periodic (each vibration making the same amount of time) back and forth oscillation In an ideal system (no friction), once simple harmonic motion is started, it would continue forever.

Examples Spring: as the spring compresses or stretches, the tension force in the spring accelerates it back toward its equilibrium position (its resting length).

Examples Pendulums: as the pendulum swings, gravity accelerates it back towards its equilibrium position Uniform circular motion: as an object moves around a circle, its vertical position (y-position) is continuously oscillating

Examples Waves: Waves passing through some medium (such as water or air) cause the medium to oscillate up and down, like a duck sitting on the water as waves pass by

Characteristics of Simple Harmonic Motion Equilibrium: the natural resting position Cycle/oscillation/wave: one complete “back and forth” from an initial point back to the same point Displacement (x): the distance moved from equilibrium position (unit=meters) Amplitude (A): the maximum displacement from equilibrium (unit=meters) Spring Constant (k): a rating of the stiffness of a spring, found using k = F ÷ x F= applied force (N) x = displacement (m) *only applies to springs

Characteristics of Simple Harmonic Motion Period (T): The time required for one cycle (unit=seconds) Frequency (f): how many complete cycles per second (unit=Hertz (Hz))

Take out. . . 1. Mass on a Spring 2. Pendulum Inquiry 3. Lab: Springs and Pendulums

On your diagrams of the pendulum and of the spring, label the following points: - Amplitude (there should be two of these points for both) - Equilibrium - Label/describe the path each travels in one time period Now, add labels for - Highest kinetic energy Lowest kinetic energy Highest potential energy Lowest potential energy Kinetic to potential conversion Potential to kinetic conversion

Energy in Simple Harmonic Motion The kinetic energy of any simple harmonic oscillator (spring, pendulum, wave) can be found using the equation KE = (½)mv 2 Pendulums have gravitational potential energy that can be found using the equation PE = mgh Springs have elastic potential energy that can be found using the equation PE = (½) kx 2 k = spring constant (stiffness of spring), measured in N/m x = displacement of spring from equilibrium (rest position) We will not do calculations with the potential energy of a wave

Waves A wave is an oscillation that travels. As energy moves through a medium ( a material), it displaces(moves) the medium. Example: A ball floating on water can oscillate up and down in harmonic motion. The surface of the water oscillates in response and the oscillation spreads outward from where it started.

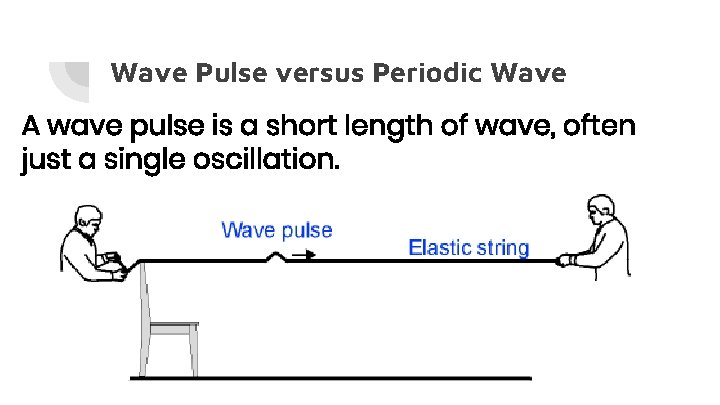
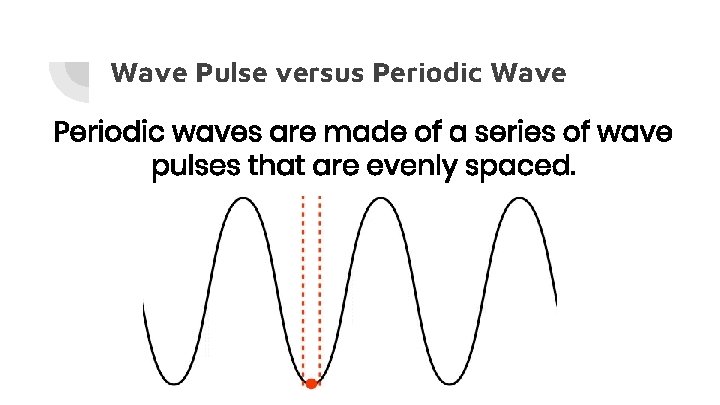
Wave Pulse versus Periodic Wave A wave pulse is a short length of wave, often just a single oscillation.

Wave Pulse versus Periodic Wave Periodic waves are made of a series of wave pulses that are evenly spaced.

Types of Waves Electromagnetic Wavewaves that do not need a medium (material) to travel Examples: radio and light waves Mechanical Wavewaves that do need a medium like wate air, or anything for it to travel. Examples: sound waves

Referring to #3 on the “Exploring Waves” interactive. . . You simulated a transverse wave. . . describe the motion of the particles in relation to the movement of the wave.

Mechanical Waves ▪ A transverse wave is created when the oscillations move perpendicular to the direction the wave moves.

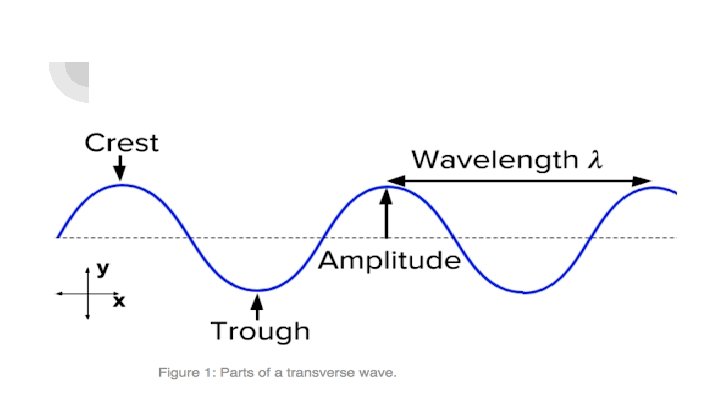
Characteristics of Transverse Waves Crest - top part of the wave Trough - bottom part of the wave The wavelength (λ) is the length of one complete cycle. Unit = meters The amplitude is the distance from the top(or bottom) to the midline of the wave. Unit = meters

On the Anatomy of a Wave sheet. . . Which wave is a transverse wave? Based on the given definitions, label the following points on the transverse wave… 1. 2. 3. 4. Crest Trough Wavelength Amplitude - draw a line to indicate what distance you would measure for an amplitude

Referring to #11 on the “Exploring Waves” interactive. . . You simulated a longitudinal wave. . . describe the motion of the particles in relation to the movement of the wave.

▪ A longitudinal wave is created when the oscillations in the same direction as the wave moves.

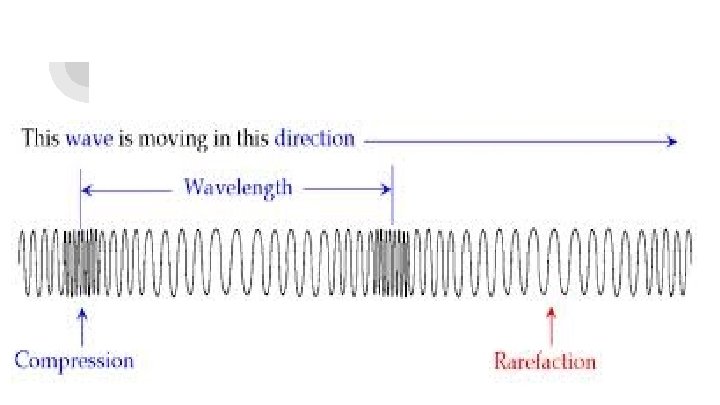
Characteristics of Longitudinal Waves Compression - particles are condensed Rarefactions - particles are stretched Wavelength - distance from one compression to the next Amplitude - how compressed or expanded the medium is

On the Anatomy of a Wave sheet. . . Which wave is a longitudinal wave? Based on the given definitions, label the following points on the longitudinal wave… 1. 2. 3. 4. Compression Rarefaction Wavelength Amplitude

Wave Speed The speed of a wave is directly related to both the frequency and the wavelength of the wave Speed of a Wave = Frequency x Wavelength