Simple Harmonic Motion Simple Harmonic Motion l Vibrations

Simple Harmonic Motion

Simple Harmonic Motion l Vibrations èVocal cords when singing/speaking èString/rubber band l Simple Harmonic Motion èRestoring force proportional to displacement èSprings F = -kx 11

Question II A mass on a spring oscillates back & forth with simple harmonic motion of amplitude A. A plot of displacement (x) versus time (t) is shown below. At what points during its oscillation is the magnitude of the acceleration of the block biggest? 1. When x = +A or -A (i. e. maximum displacement) 2. When x = 0 (i. e. zero displacement) 3. The acceleration of the mass is constant +A x t -A 17

Potential Energy in Spring l Force of spring is Conservative èF = -k x èW = -1/2 k x 2 Force work x èWork done only depends on initial and final position èDefine Potential Energy PEspring = ½ k x 2 20

***Energy in SHM*** l. A mass is attached to a spring and set to motion. The maximum displacement is x=A èEnergy = PE + KE = constant! = ½ k x 2 + ½ m v 2 èAt maximum displacement x=A, v = 0 PES 2 Energy = ½ k A + 0 èAt zero displacement x = 0 Energy = 0 + ½ mvm 2 Since Total Energy is same 0 2 2 ½ k A = ½ m vm = sqrt(k/m) A x=0 x x 25

Question 3 A mass on a spring oscillates back & forth with simple harmonic motion of amplitude A. A plot of displacement (x) versus time (t) is shown below. At what points during its oscillation is the speed of the block biggest? 1. When x = +A or -A (i. e. maximum displacement) 2. When x = 0 (i. e. zero displacement) 3. The speed of the mass is constant +A x t -A 29

Question 4 l A spring oscillates back and forth on a frictionless horizontal surface. A camera takes pictures of the position every 1/10 th of a second. Which plot best shows the positions of the mass. 1 End. Point Equilibrium End. Point 2 3 38

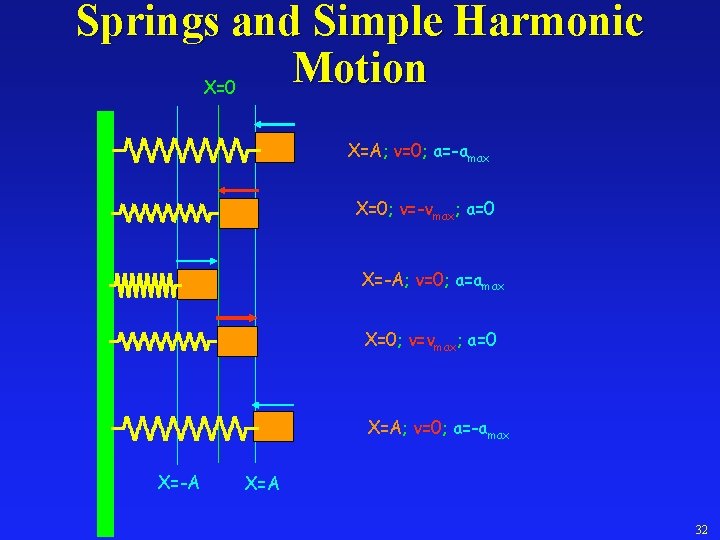
Springs and Simple Harmonic Motion X=0 X=A; v=0; a=-amax X=0; v=-vmax; a=0 X=-A; v=0; a=amax X=0; v=vmax; a=0 X=A; v=0; a=-amax X=-A X=A 32

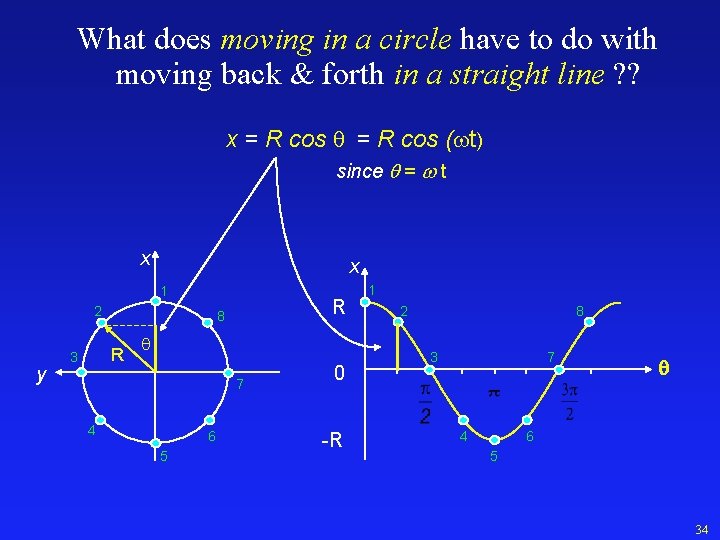
What does moving in a circle have to do with moving back & forth in a straight line ? ? x = R cos q = R cos ( t) since q = w t x x 1 2 y R 3 R 8 q 7 4 6 5 0 -R 1 2 8 7 3 4 6 5 34

SHM and Circles

Simple Harmonic Motion: x(t) = [A]cos( t) v(t) = -[A ]sin( t) a(t) = -[A 2]cos( t) x(t) = [A]sin( t) OR v(t) = [A ]cos( t) a(t) = -[A 2]sin( t) xmax = A Period = T (seconds per cycle) vmax = A Frequency = f = 1/T (cycles per second) amax = A 2 Angular frequency = = 2 f = 2 /T For spring: 2 = k/m 36

Example A 3 kg mass is attached to a spring (k=24 N/m). It is stretched 5 cm. At time t=0 it is released and oscillates. Which equation describes the position as a function of time x(t) = A) 5 sin( t) B) 5 cos( t) C) 24 sin( t) D) 24 cos( t) E) -24 cos( t) 39

Example A 3 kg mass is attached to a spring (k=24 N/m). It is stretched 5 cm. At time t=0 it is released and oscillates. What is the total energy of the block spring system? 43

Example A 3 kg mass is attached to a spring (k=24 N/m). It is stretched 5 cm. At time t=0 it is released and oscillates. What is the maximum speed of the block? 46

Example A 3 kg mass is attached to a spring (k=24 N/m). It is stretched 5 cm. At time t=0 it is released and oscillates. How long does it take for the block to return to x=+5 cm? 49

Pendulum Motion l For small angles èT = mg èTx = -mg (x/L) Note: F proportional to x! èS Fx = m ax -mg (x/L) = m ax ax = -(g/L) x èRecall for SHO a = - 2 x = sqrt(g/L) T = 2 sqrt(L/g) Period does not depend on A, or m! L T x m mg 37

Example: Clock l If we want to make a grandfather clock so that the pendulum makes one complete cycle each sec, how long should the pendulum be?

Question 1 Suppose a grandfather clock (a simple pendulum) runs slow. In order to make it run on time you should: 1. Make the pendulum shorter 2. Make the pendulum longer 38

Summary l Simple Harmonic Motion èOccurs when have linear restoring force F= -kx èx(t) = [A] cos( t) èv(t) = -[A ] sin( t) èa(t) = -[A 2] cos( t) l Springs èF = -kx èU = ½ k x 2 è = sqrt(k/m) l Pendulum (Small oscillations) è = sqrt(L/g) 50