Simple Harmonic Motion AP Physics C Mrs Coyle








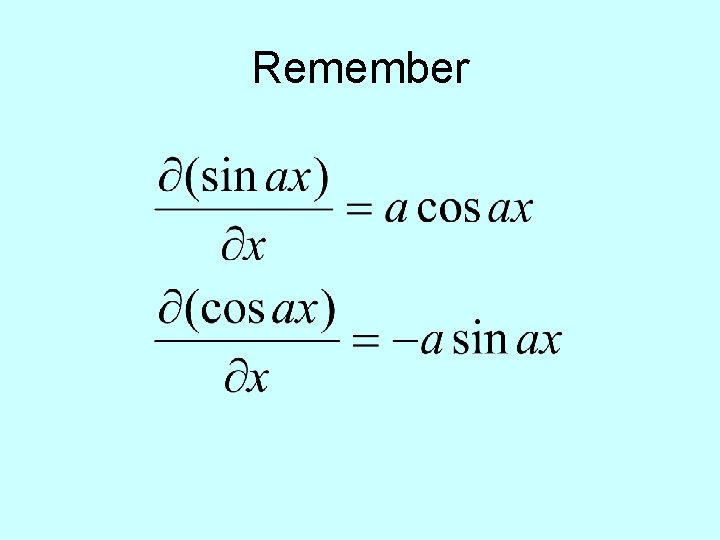

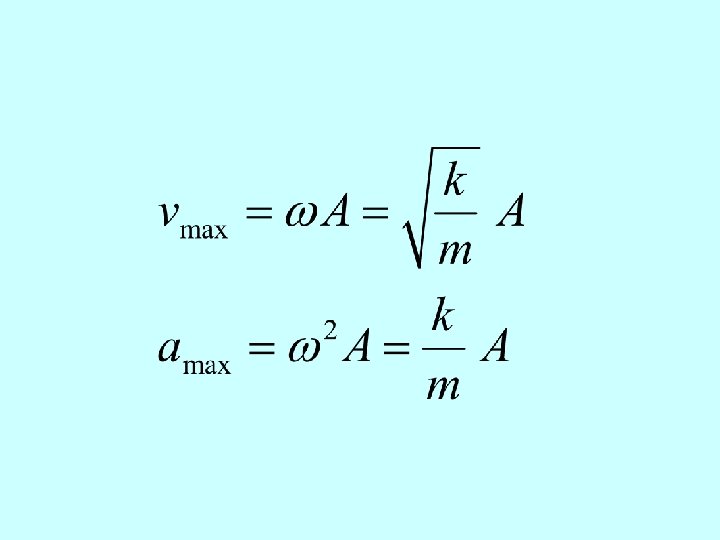



- Slides: 24

Simple Harmonic Motion AP Physics C Mrs. Coyle

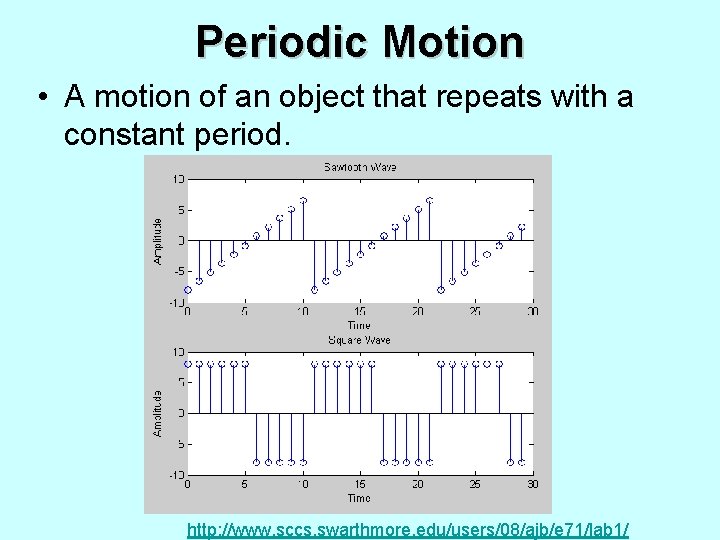
Periodic Motion • A motion of an object that repeats with a constant period. http: //www. sccs. swarthmore. edu/users/08/ajb/e 71/lab 1/

Simple Harmonic Motion • It is a periodic motion. AND • It has a restoring force that acts to restore the oscillator to equilibrium. The restoring force is given by: Hooke’s Law F=-kx x is the displacement from equilibrium and k is the force constant (spring constant). • The period of SHM oscillator does not depend on the amplitude.

Simple Harmonic Motion Simulations http: //bcs. wiley. com/hebcs/Books? action=mininav&bcs. Id=3606&it em. Id=0471758019&asset. Id=111700&reso urce. Id=10211 -SHM -Particle oscillating in SHM

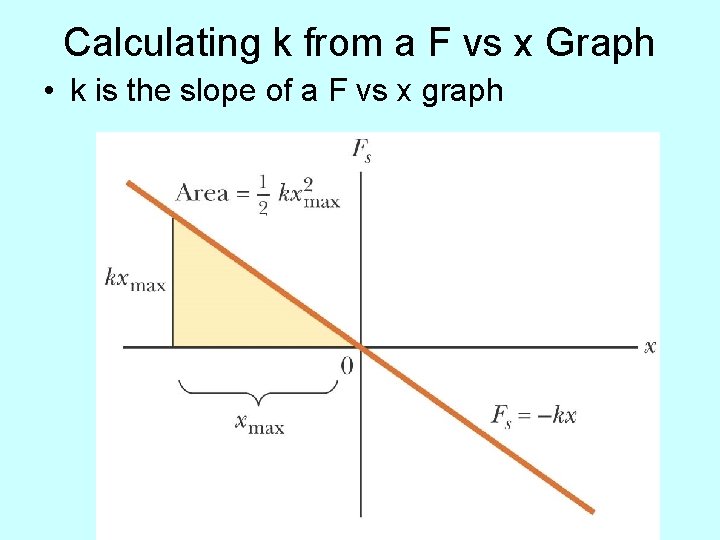
Calculating k from a F vs x Graph • k is the slope of a F vs x graph

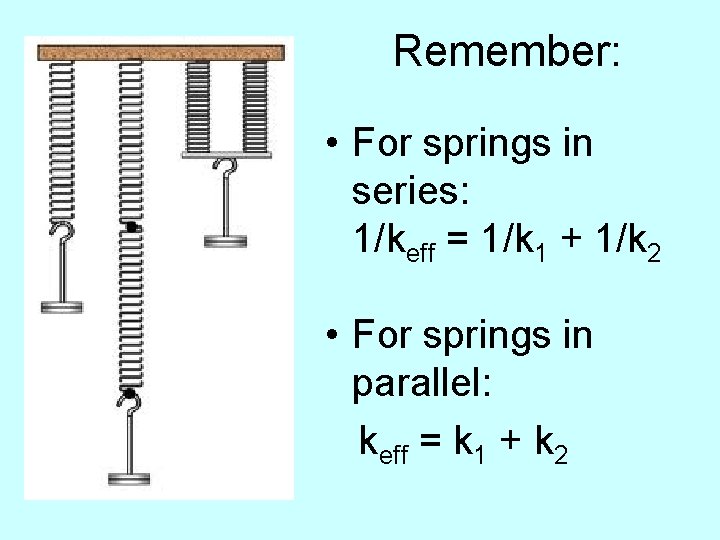
Remember: • For springs in series: 1/keff = 1/k 1 + 1/k 2 • For springs in parallel: keff = k 1 + k 2

The acceleration in SHM is not constant:

Acceleration in Simple Harmonic Motion • Acceleration • Let • a = - w 2 x

Characteristic Quantities of Simple Harmonic Motion • Displacement • Amplitude: maximum displacement • Frequency • Period • f=1/T T=1/f

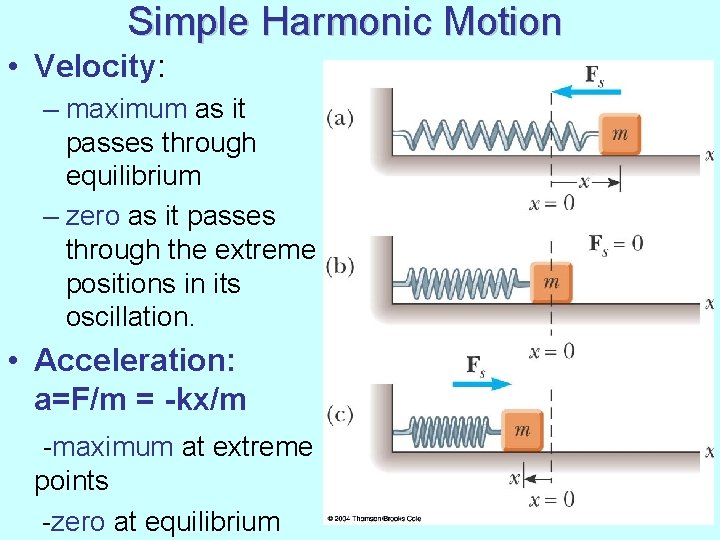
Simple Harmonic Motion • Velocity: – maximum as it passes through equilibrium – zero as it passes through the extreme positions in its oscillation. • Acceleration: a=F/m = -kx/m -maximum at extreme points -zero at equilibrium

Equations of Motion. Displacement • x=Asin(wt +f) • x=-Asin(wt +f) or x=Acos(wt +f) x=-Acos(wt +f) • w=angular frequency, rad/s • f is the phase constant

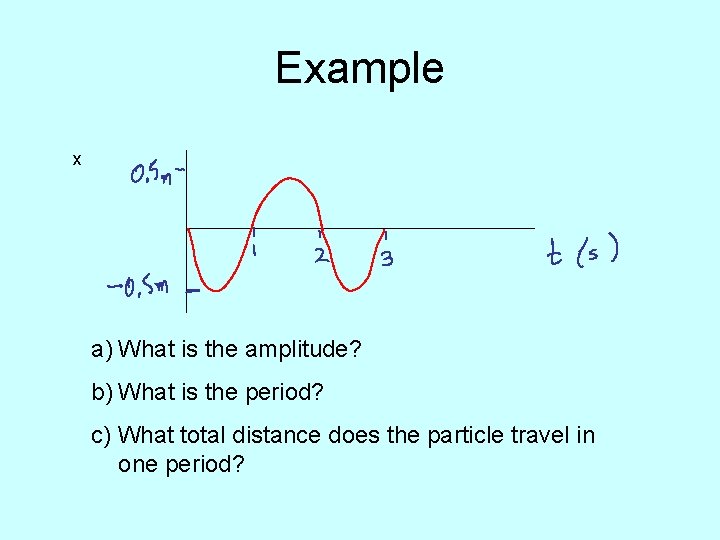
Example x a) What is the amplitude? b) What is the period? c) What total distance does the particle travel in one period?

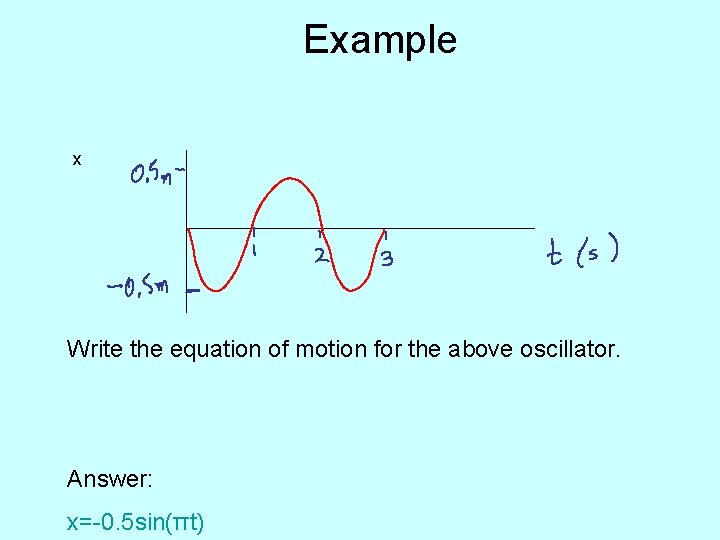
Example x Write the equation of motion for the above oscillator. Answer: x=-0. 5 sin(πt)

Note • The acceleration is not constant and therefore the kinematics equations cannot be used. There are two options: 1. Use conservation of mechanical energy to find v at a given position. E= ½ mv 2 + ½ kx 2 = constant or 2. Take the first derivative of x (equation of motion) to find v and the second derivative to find a.
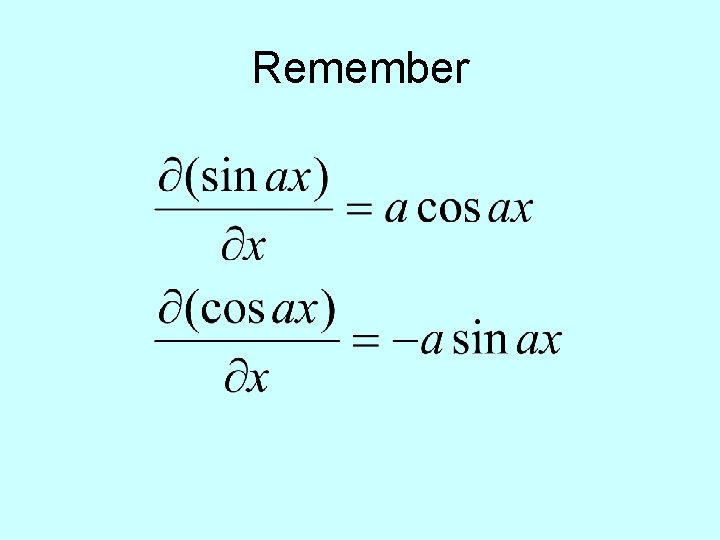
Remember

Examples of Motion Equations for Simple Harmonic Motion
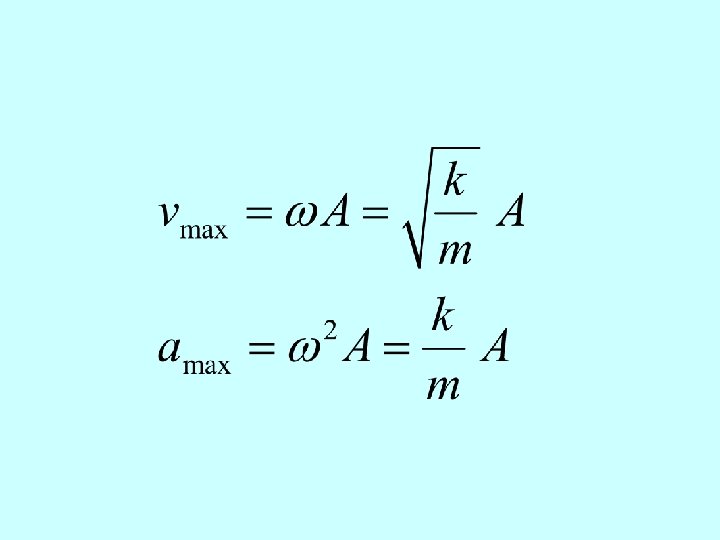

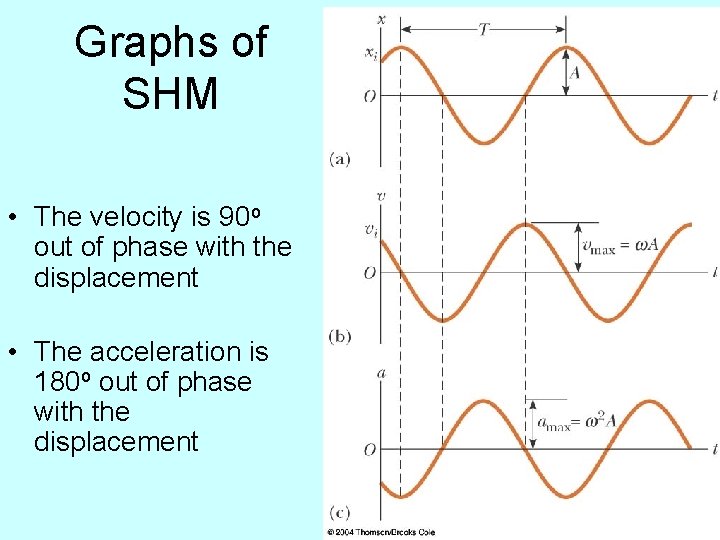
Graphs of SHM • The velocity is 90 o out of phase with the displacement • The acceleration is 180 o out of phase with the displacement

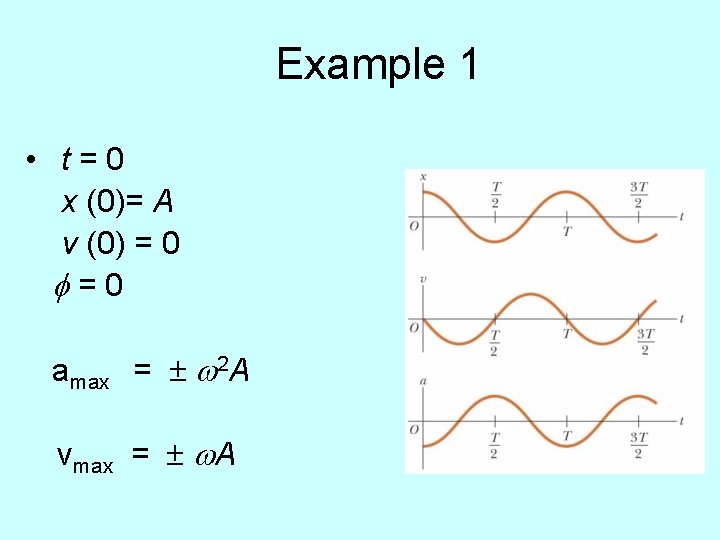
Example 1 • t=0 x (0)= A v (0) = 0 f=0 amax = ± w 2 A vmax = ± w. A

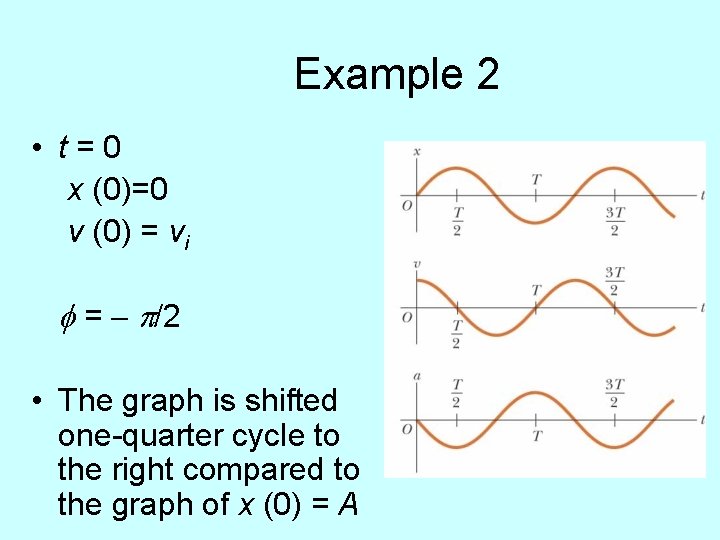
Example 2 • t=0 x (0)=0 v (0) = vi f = - p/2 • The graph is shifted one-quarter cycle to the right compared to the graph of x (0) = A

Period and Frequency

Period of A Spring Mass Oscillator ____ • T=2 p√m/k • • m mass k spring constant T does not depend on g The period is smaller for a stiffer spring (large values of k).

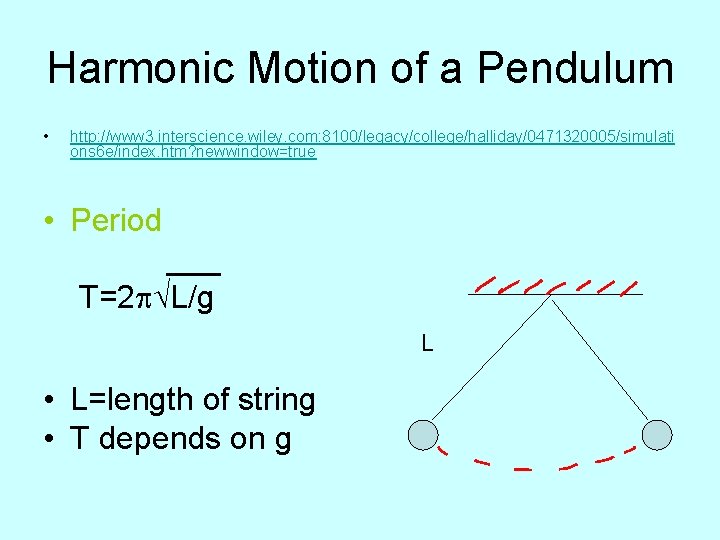
Harmonic Motion of a Pendulum • http: //www 3. interscience. wiley. com: 8100/legacy/college/halliday/0471320005/simulati ons 6 e/index. htm? newwindow=true • Period ___ T=2 p√L/g L • L=length of string • T depends on g

Question • If you had a spring-mass system on the moon, would the period be the same or different than that of this system on the earth? • What if it were a pendulum system?