String instruments and harmonic frequencies String wave Speed


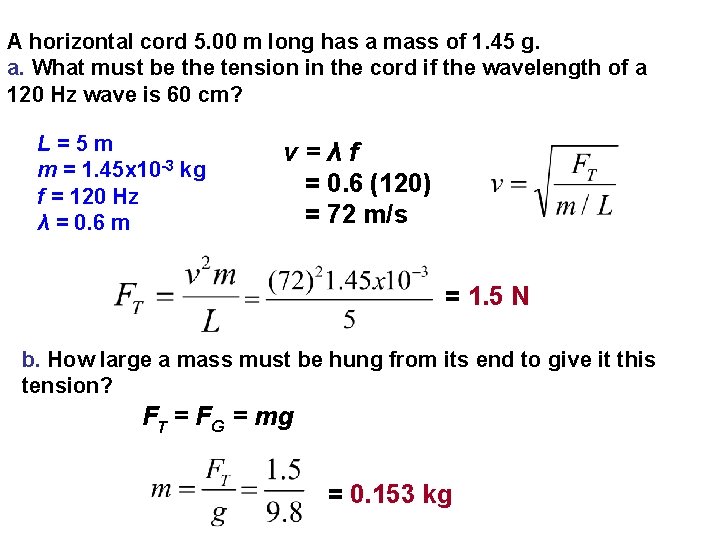



















- Slides: 32

String instruments and harmonic frequencies

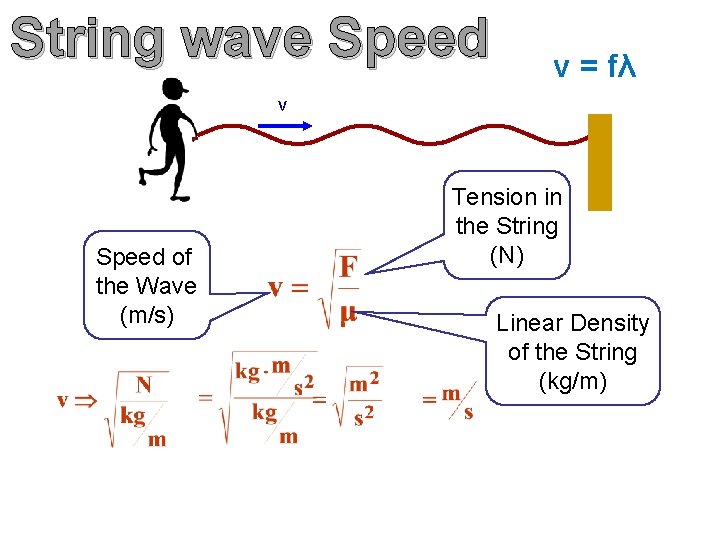
String wave Speed v = fλ v Speed of the Wave (m/s) Tension in the String (N) Linear Density of the String (kg/m)

Standing waves_tension plus

A transverse wave is moving along a string whose tension is 10 N. The speed of the wave is 200 m/s. What will the speed be if the tension is increased to 40 N? a)100 m/s b) 50 m/s c) 200 m/s d) 400 m/s e) 800 m/s
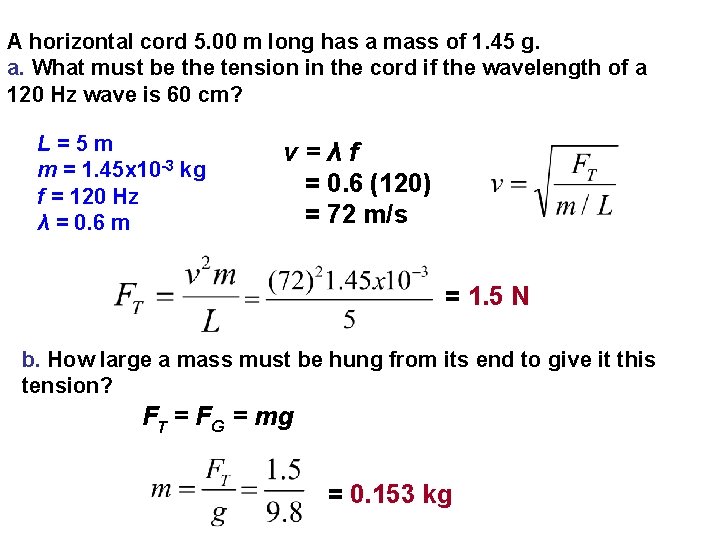
A horizontal cord 5. 00 m long has a mass of 1. 45 g. a. What must be the tension in the cord if the wavelength of a 120 Hz wave is 60 cm? L=5 m m = 1. 45 x 10 -3 kg f = 120 Hz λ = 0. 6 m v = λ f = 0. 6 (120) = 72 m/s = 1. 5 N b. How large a mass must be hung from its end to give it this tension? FT = FG = mg = 0. 153 kg

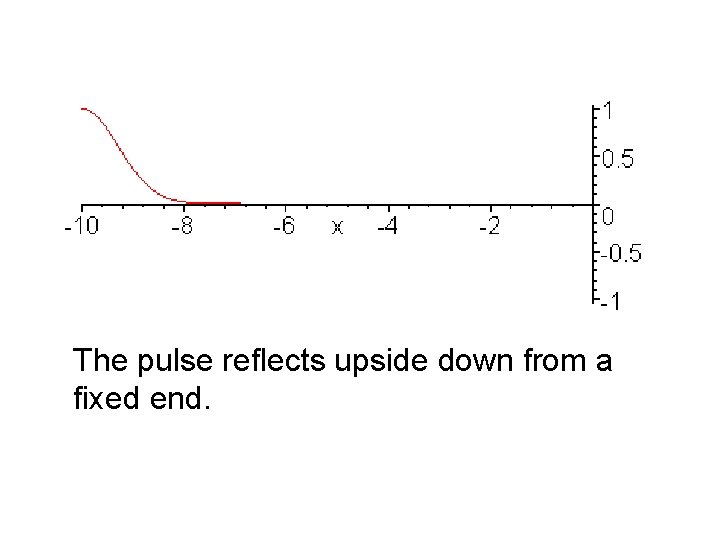
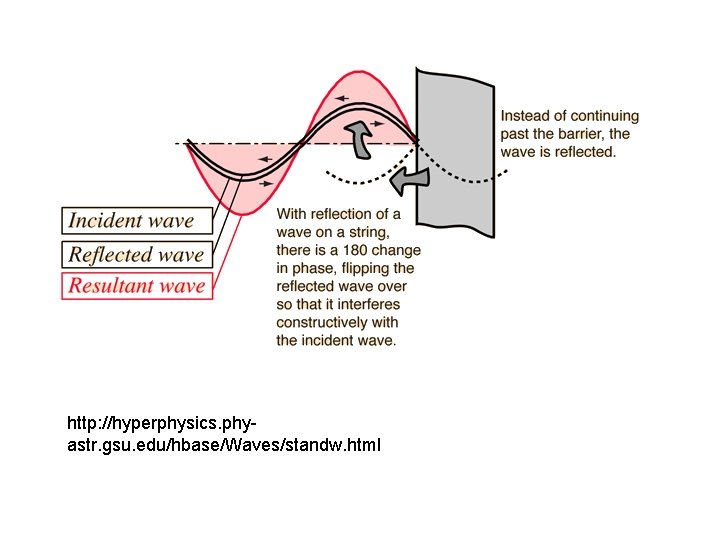
The pulse reflects upside down from a fixed end.

http: //hyperphysics. phyastr. gsu. edu/hbase/Waves/standw. html

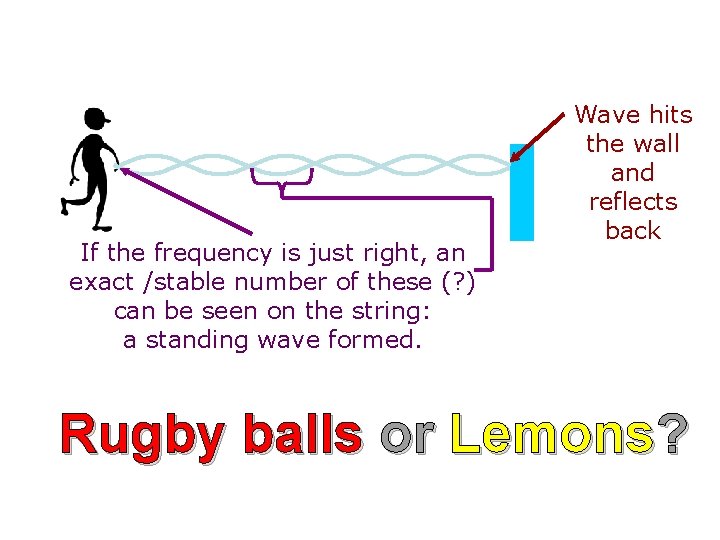
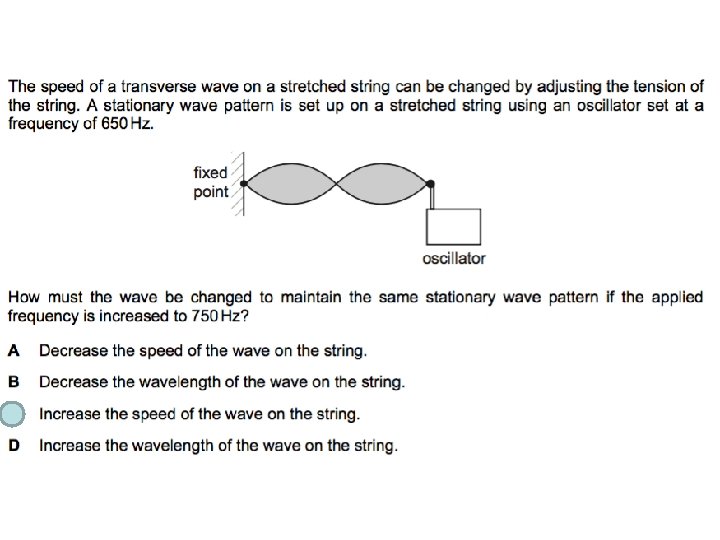
If the frequency is just right, an exact /stable number of these (? ) can be seen on the string: a standing wave formed. Wave hits the wall and reflects back Rugby balls or Lemons?

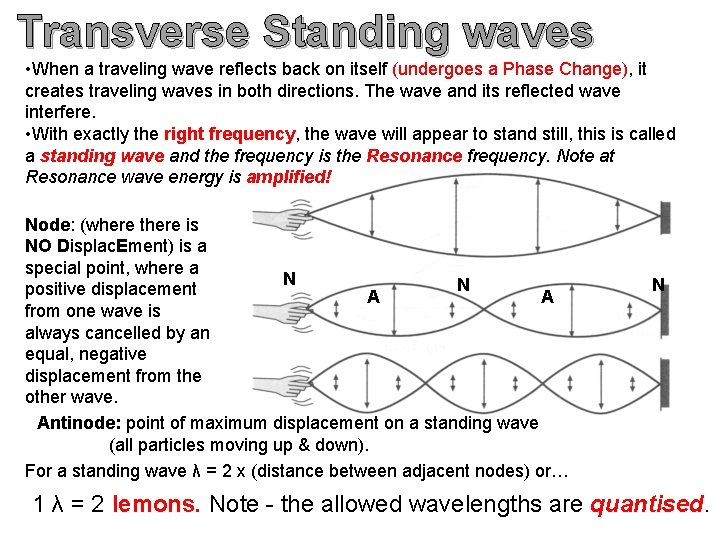
Transverse Standing waves • When a traveling wave reflects back on itself (undergoes a Phase Change), it creates traveling waves in both directions. The wave and its reflected wave interfere. • With exactly the right frequency, the wave will appear to stand still, this is called a standing wave and the frequency is the Resonance frequency. Note at Resonance wave energy is amplified! Node: (where there is NO Displac. Ement) is a special point, where a N N positive displacement A A from one wave is always cancelled by an equal, negative displacement from the other wave. Antinode: point of maximum displacement on a standing wave (all particles moving up & down). For a standing wave λ = 2 x (distance between adjacent nodes) or… N 1 λ = 2 lemons. Note - the allowed wavelengths are quantised.


Sources of Sound: Vibrating Strings The length of string that vibrates is determined by finger placement. The placement determines the wavelength and pitch (frequency) of the sound formed. The pitch of a string of a given length can also be altered by changing the string density or tension that the string is under. Physics Guitar demo


A standing wave is produced by the superposition of two periodic waves having identical frequencies which are traveling in opposite directions. In stringed musical instruments, the standing wave is produced by waves reflecting off a fixed end and interfering with oncoming waves as they travel back through the medium.

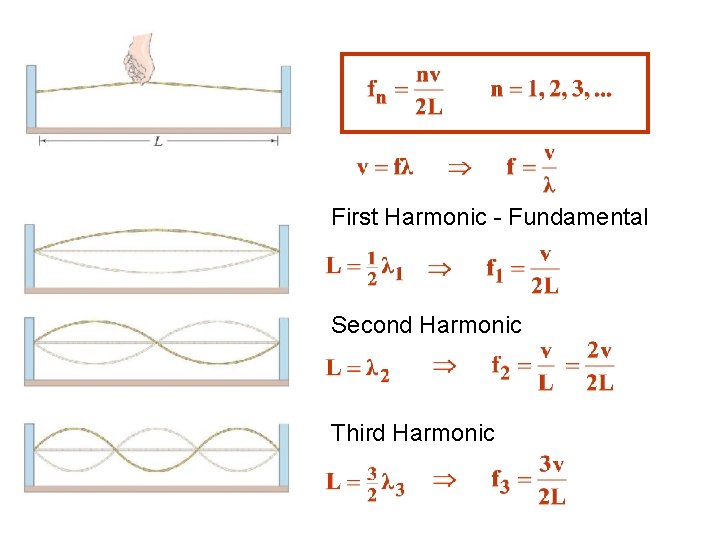
There can be more than one frequency for standing waves. Frequencies at which standing waves can be produced are called the resonant (harmonic) frequencies. When a string on an instrument is plucked, vibrations, that is, waves, travel back and forth through the medium being reflected at each fixed end. Certain sized waves can survive on the medium. These certain sized waves will not cancel each other out as they reflect back upon themselves. These certain sized waves are called the harmonics of the vibration. They are standing waves. That is, they produce patterns which do not move.


First Harmonic - Fundamental Second Harmonic Third Harmonic

Thingee Activity: Determine the wave frequency of a Thingee wave TTD: • Derive your own method • Algebraic expression • Variables • IDV • CVs or constants • Use V= fλ & • Enquiry: solve for 1 st or 2 nd Harmonic?


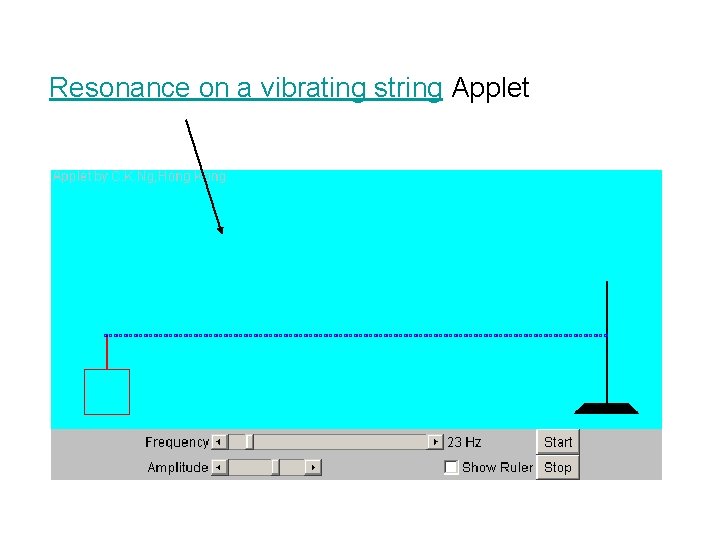
Resonance on a vibrating string Applet

Guitar String If I press my finger on a string, it makes the string shorter. What does that do to the frequency, and the perceived pitch (note)? A. Frequency: increases Pitch: raises B. Frequency: increases Pitch: lowers C. Frequency: decreases. Pitch: raises D. Frequency: decreases. Pitch: lowers E. None of these

Guitar String When I tighten a string, what does that do to the frequency, and why? A. Increases, because the speed of the wave increases B. Increases, because it is a higher harmonic C. Increases because the length of the string increases D. Decreases because the length of the string increases E. None of these

What is the fundamental frequency of a viola string that is 35. 0 cm long when the speed of waves on this string is 346 m/s? L = 0. 35 m v = 346 m/s L= 1/2 λ and λ = 2 L = 494. 2 Hz



A metal string is under a tension of 88. 2 N. Its length is 50 cm and its mass is 0. 500 g. a. Find the velocity of the waves on the string. m = 5 x 10 -4 kg FT = 88. 2 N L = 0. 5 m = 297 m/s b. Determine the frequencies of its fundamental, first overtone and second overtone. Fundamental: L = 1/2 λ λ = 2 L = 2(0. 5) =1 m = 297 Hz

First overtone fn = n f' f 2 = 2(297) = 594 Hz Second overtone fn = n f' f 3 = 3(297) = 891 Hz

A string 2. 0 m long is driven by a 240 Hz vibrator at its end. The string resonates in four segments. What is the speed of the waves on the string? L = 2 m f = 240 Hz 4 segments: 4 th Harmonic L = 4/2 λ = 2 λ λ = ½ L = ½ (2) = 1 m v = f λ = 240 (1) = 240 m/s

A banjo string 30 cm long resonates in its fundamental to a frequency of 256 Hz. What is the speed of the waves on the string? L = 0. 3 m f = 256 Hz Fundamental: L = ½ λ λ = 2 L = 2(0. 3) = 0. 6 m v = f λ = 256 (0. 6) = 154 m/s

A string vibrates in five segments to a frequency of 460 Hz. a. What is its fundamental frequency? f 5 = 460 Hz fn = n f' = 92 Hz b. What frequency will cause it to vibrate in three segments? fn = n f' f 3 = 3(92) = 276 Hz



Closed End Transverse waves N N A Meter ruler demo # of Rugby balls ? A