Rotation Kinematics NEED FOR ANGULAR QUANTITIES In rotation












- Slides: 16

Rotation Kinematics

NEED FOR ANGULAR QUANTITIES In rotation the axis of rotation is physically located on the object. All points on a rotating system have different velocities. All points on a radial line (along a radius) have the same instantaneous direction, but different speeds. All points the same distance from the axis have the same speeds, but have different directions.

NEED FOR ANGULAR QUANTITIES Examine four points. The time required to move the distances shown is the same for all four points. However, points more distant from the axis must travel farther. A B C These points must have greater speed. Therefore, linear distance and tangential speed cannot be used to describe the motion of all the points simultaneously. However, there is a quantity that all points on a rotating system share. All points on a rotating system move through the same angle in a time t. D

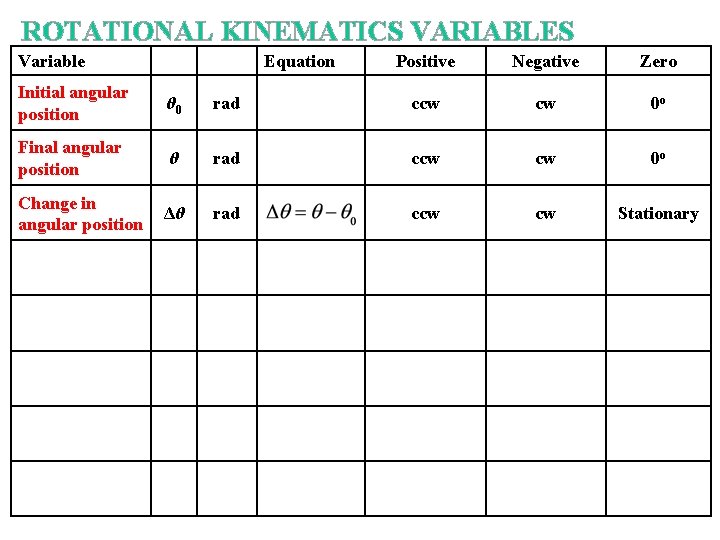
NEED FOR ANGULAR QUANTITIES During rotation, objects move θ from in initial angle θ 0 to a final angle θ Experiencing and angular displacement Δθ. All angular quantities are in radians. Δθ θ 0

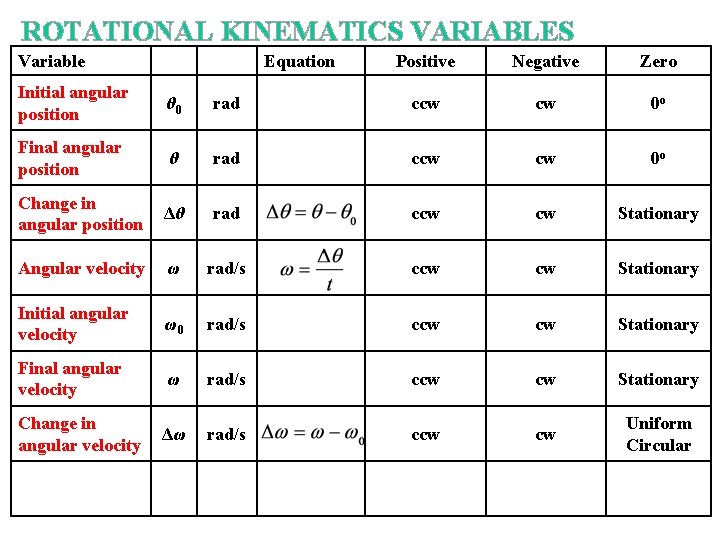
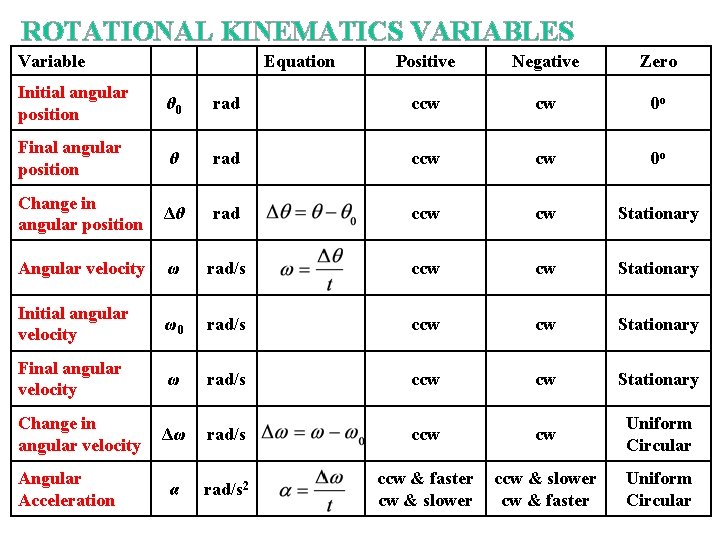
ROTATIONAL KINEMATICS VARIABLES Variable Equation Positive Negative Zero

ROTATIONAL KINEMATICS VARIABLES Variable Equation Positive Negative Zero Initial angular position θ 0 rad ccw cw 0 o Final angular position θ rad ccw cw 0 o Δθ rad ccw cw Stationary Change in angular position

ROTATIONAL KINEMATICS VARIABLES Variable Equation Positive Negative Zero Initial angular position θ 0 rad ccw cw 0 o Final angular position θ rad ccw cw 0 o Change in angular position Δθ rad ccw cw Stationary Angular velocity ω rad/s ccw cw Stationary Initial angular velocity ω0 rad/s ccw cw Stationary Final angular velocity ω rad/s ccw cw Stationary Δω rad/s ccw cw Uniform Circular Change in angular velocity

ROTATIONAL KINEMATICS VARIABLES Variable Equation Positive Negative Zero Initial angular position θ 0 rad ccw cw 0 o Final angular position θ rad ccw cw 0 o Change in angular position Δθ rad ccw cw Stationary Angular velocity ω rad/s ccw cw Stationary Initial angular velocity ω0 rad/s ccw cw Stationary Final angular velocity ω rad/s ccw cw Stationary Δω rad/s ccw cw Uniform Circular α rad/s 2 ccw & faster cw & slower cw & faster Uniform Circular Change in angular velocity Angular Acceleration

ROTATIONAL KINEMATIC EQUATIONS Kinematic Equation

ROTATIONAL KINEMATIC EQUATIONS Kinematic Equation In terms of Δθ When ω0 = 0 Strategy Not relevant Use if problem states uniform circular motion (constant speed) Time is not mentioned, or the variables to solve time are missing Time and angular displacement (or angular position) are mentioned Time and angular velocity are mentioned

CONVERSIONS θ The angle of the rotation (rad) ω The angular velocity (rad/s) α The angular acceleration (rad/s 2) The number of cycles (revolutions, rotations, orbits, etc. ) is tied to the angular displacement. To convert between cycles and Δθ … rpm’s (revolutions per minute) is tied to angular velocity. Converting angular quantities into tangential quantities.

Example 1 An object rotates with a constant angular speed. It completes 10 rev in 2. 0 s. Determine each of the following for a point P, that is 4. 0 m from the axis. (A) angular displacement (B) tangential displacement (C) angular velocity (D) tangential velocity

Example 1 An object rotates with a constant angular speed. It completes 10 rev in 2. 0 s. Determine the object’s (E) angular acceleration (F) tangential acceleration (G) radial acceleration

Example 2 Δθ ω0 ω α t An object initially at rest rotates with an angular acceleration of 6. 0 rad/s 2. How many revolutions has the object completed when it reaches the point where it is spinning at 120 rpm? = = 0 rad/s = 12. 6 rad/s = 6. 0 rad/s 2 = 120 rpm’s can be converted into angular velocity. Angular displacement can be converted into revolutions.

Example 3 An object with an initial angular velocity of 20 rad/s accelerates at 10 rad/s 2 for 5. 0 s. Determine the object’s (A) angular displacement Δθ 230=rad ω0 = 20 rad/s ω = α = 10 rad/s 2 (B) of a point 3. 0 m from the axis t radial = acceleration 5. 0 s Need tangential velocity, but have radial variables. Now you can solve for radial accel.

Example 4 An object initially at rest rotates with a uniform angular acceleration. After 10 seconds a point 3. 0 m from the axis has a tangential speed of 20 m/s. Determine the object’s (A) final angular velocity Δθ (B) angular acceleration = ω0 =0 rad/s 5. 0 rad/s ω 0. 5 =rad/s 2 α = t = 10 s (C) radial acceleration (D) angular displacement