Solving Quadratics Quadratic Formula Discriminant Nature of the






































- Slides: 50

Solving Quadratics Quadratic Formula Discriminant – Nature of the Roots

Warm Up – Question 1 o Given o and o find an expression for the composite function and state its domain restrictions.

Warm Up Answer

Warm Up – Question 2 o Given a) b)



Solve by Quadratic Formula

Derive the Quadratic Formula by Completing the Square

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

Solve using the Quadratic Formula

The Discriminant The nature of the roots

The Discriminant o o It comes from the quadratic formula. =

o When you apply the quadratic formula to any quadratic equation, you will find that the value of b²-4 ac is either positive, negative, or 0. o The value of the discriminant is what tells us the nature of the roots (solutions) to the quadratic.

Solutions of a Quadratic Equation o If

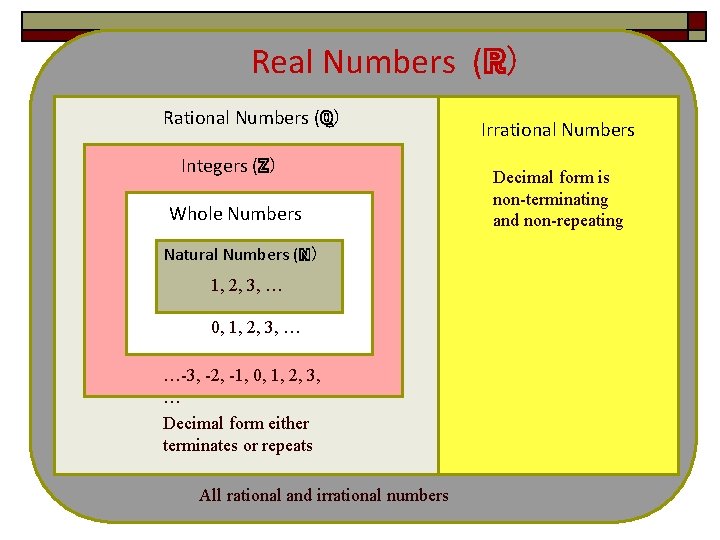
Real Numbers (ℝ) Rational Numbers (ℚ) Integers (ℤ) Whole Numbers Natural Numbers (ℕ) 1, 2, 3, … 0, 1, 2, 3, … …-3, -2, -1, 0, 1, 2, 3, … Decimal form either terminates or repeats All rational and irrational numbers Irrational Numbers Decimal form is non-terminating and non-repeating

Find the Discriminant and Describe its Roots. o Nature of the Roots

Find the Discriminant and Describe its Roots. o Nature of the Roots

Find the Discriminant and Describe its Roots o Nature of the Roots

Graphs of Polynomial Functions

Explore – Look at the relationship between the degree & sign of the leading coefficient and the right- and left-hand behavior of the graph of the function.

Explore – Look at the relationship between the degree & sign of the leading coefficient and the right- and left-hand behavior of the graph of the function.

Explore – Look at the relationship between the degree & sign of the leading coefficient and the right- and left-hand behavior of the graph of the function.

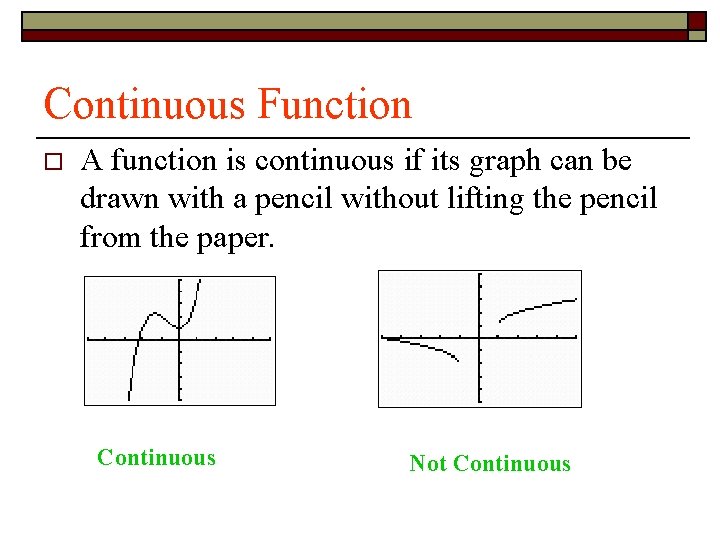
Continuous Function o A function is continuous if its graph can be drawn with a pencil without lifting the pencil from the paper. Continuous Not Continuous

Polynomial Function o Polynomial Functions have continuous graphs with smooth rounded turns. o Written: o Example:

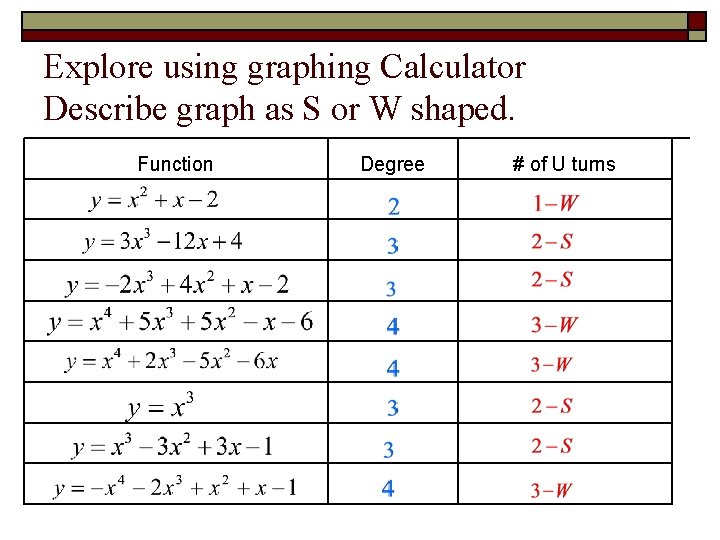
Explore using graphing Calculator Describe graph as S or W shaped. Function Degree # of U turns

Generalizations? o The number of turns is one less than the degree. o Even degree → “W” Shape o Odd degree → “S” Shape

Describe the Shape and Number of Turns.

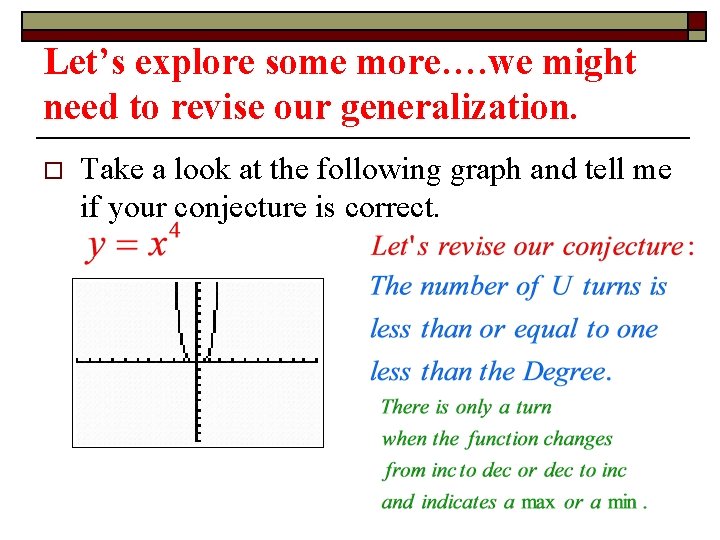
Let’s explore some more…. we might need to revise our generalization. o Take a look at the following graph and tell me if your conjecture is correct.

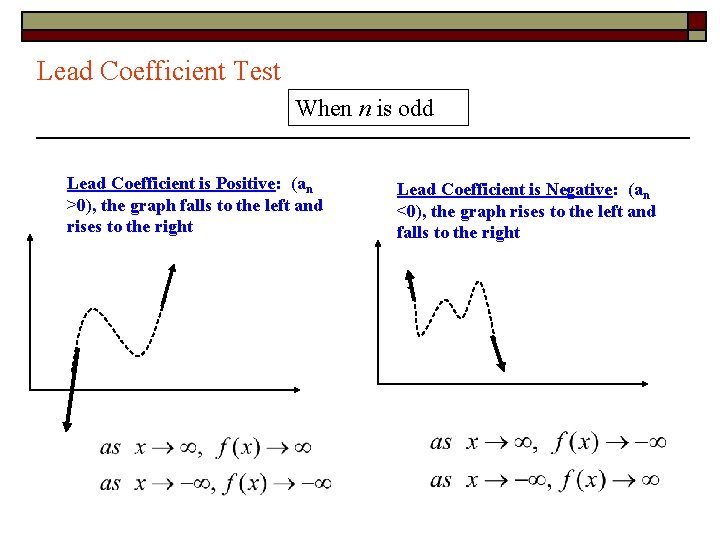
Lead Coefficient Test When n is odd Lead Coefficient is Positive: (an >0), the graph falls to the left and rises to the right Lead Coefficient is Negative: (an <0), the graph rises to the left and falls to the right

Lead Coefficient Test When n is even Lead Coefficient is Positive: (an >0), the graph rises to the left and rises to the right Lead Coefficient is Negative: (an <0), the graph falls to the left and falls to the right

Leading Coefficient: an End Behavior - a>0 a<0 left right n - even n - odd

Use the Leading Coeffiicent Test to describe the right-hand left-hand behavior of the graph of each polynomial function:

Use the Leading Coeffiicent Test to describe the right-hand left-hand behavior of the graph of each polynomial function:

Use the Leading Coeffiicent Test to describe the right-hand left-hand behavior of the graph of each polynomial function:

Use the Leading Coeffiicent Test to describe the right-hand left-hand behavior of the graph of each polynomial function:

A polynomial function (f) of degree n , the following are true o The function has at most n real zeros o The graph has at most (n-1) relative extrema (relative max/min)

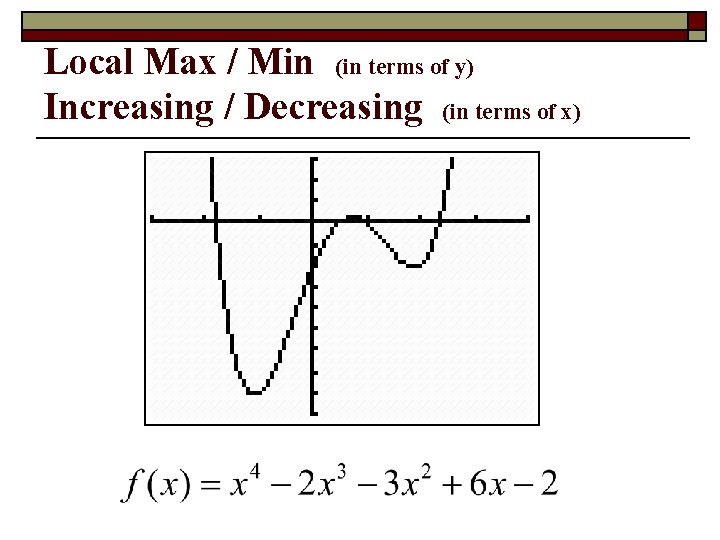
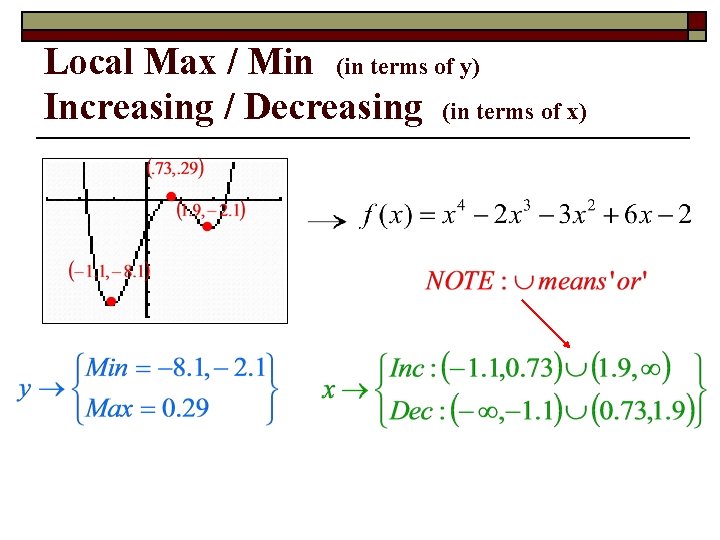
Local Max / Min (in terms of y) Increasing / Decreasing (in terms of x)

Local Max / Min (in terms of y) Increasing / Decreasing (in terms of x)

Approximate any local maxima or minima to the nearest tenth. Find the intervals over which the function is increasing and decreasing.

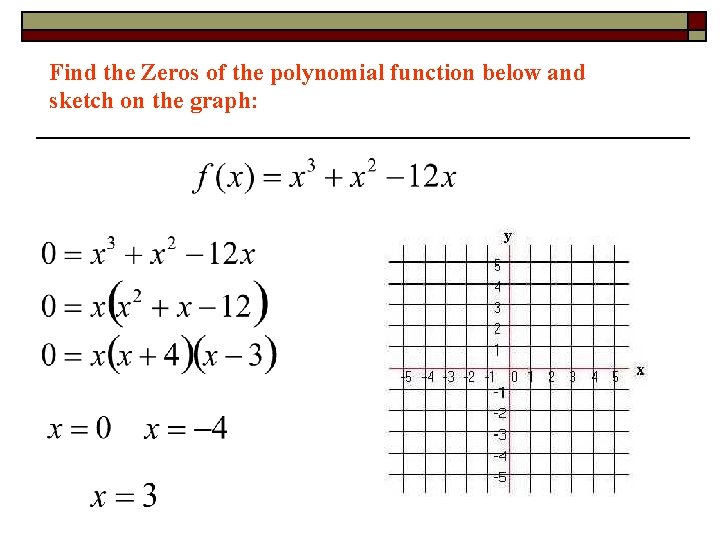
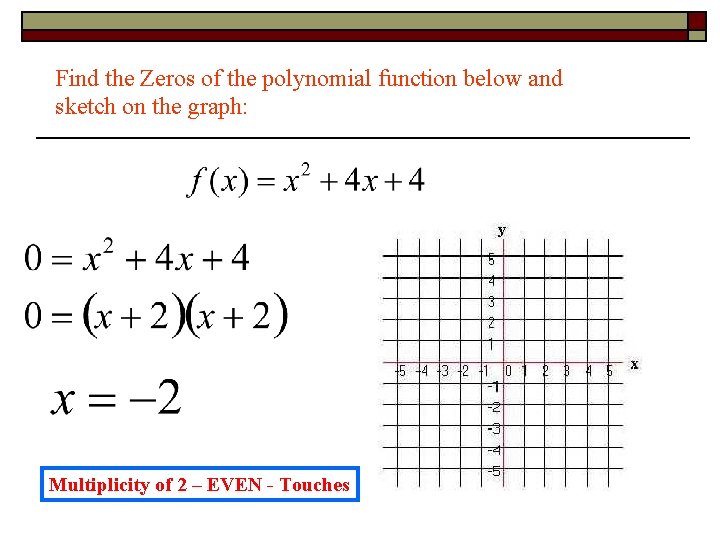
Find the Zeros of the polynomial function below and sketch on the graph:

Find the Zeros of the polynomial function below and sketch on the graph: Multiplicity of 2 – EVEN - Touches

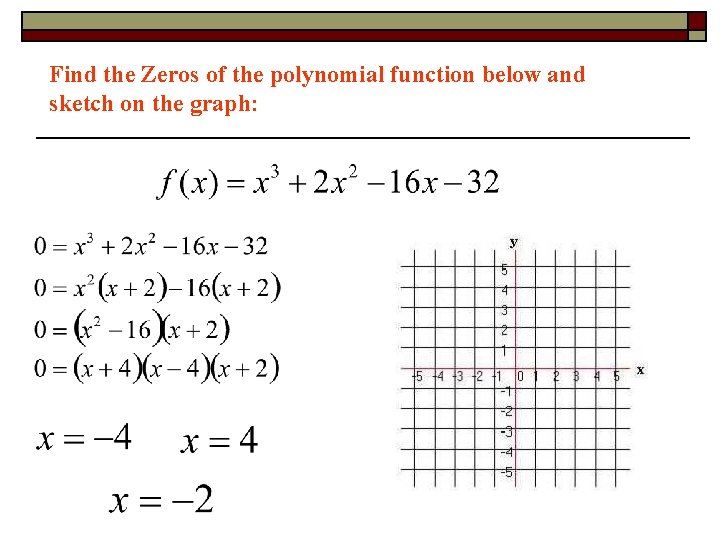
Find the Zeros of the polynomial function below and sketch on the graph:

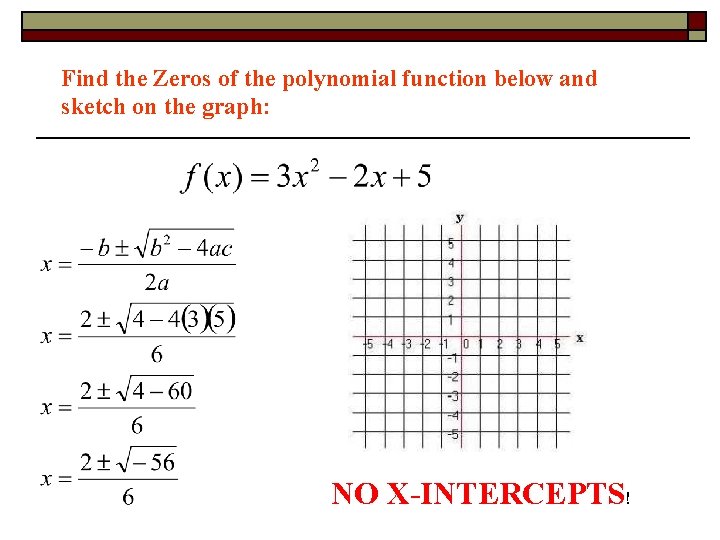
Find the Zeros of the polynomial function below and sketch on the graph: NO X-INTERCEPTS!

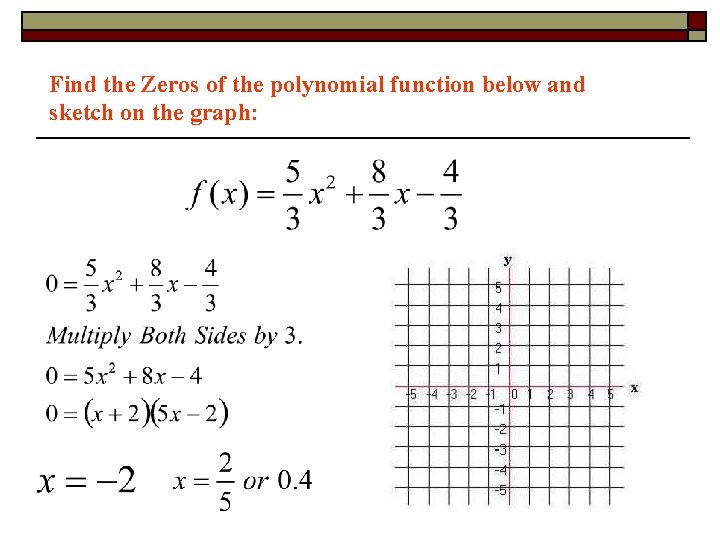
Find the Zeros of the polynomial function below and sketch on the graph: