Notes Graphing Quadratic Functions and solving quadratic linear

Notes: Graphing Quadratic Functions and solving quadratic linear systems algebraically Aim: Students will be able to solve quadratic linear systems graphically and algebraically. Grab your foldable that I gave you from class today and start filling in your notes. Happy “foldabling”.

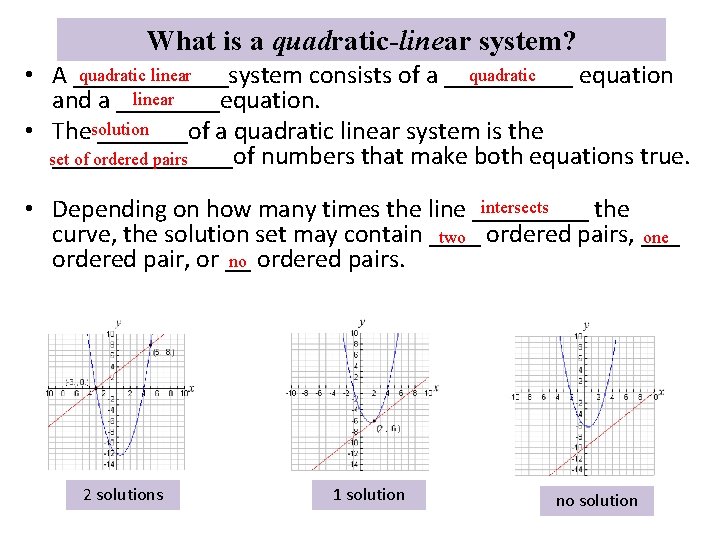
What is a quadratic-linear system? quadratic linear quadratic • A ______system consists of a _____ equation linear and a ____equation. • Thesolution _______of a quadratic linear system is the _______of numbers that make both equations true. set of ordered pairs intersects • Depending on how many times the line _____ the curve, the solution set may contain ____ two ordered pairs, ___ one ordered pair, or __ no ordered pairs. 2 solutions 1 solution no solution

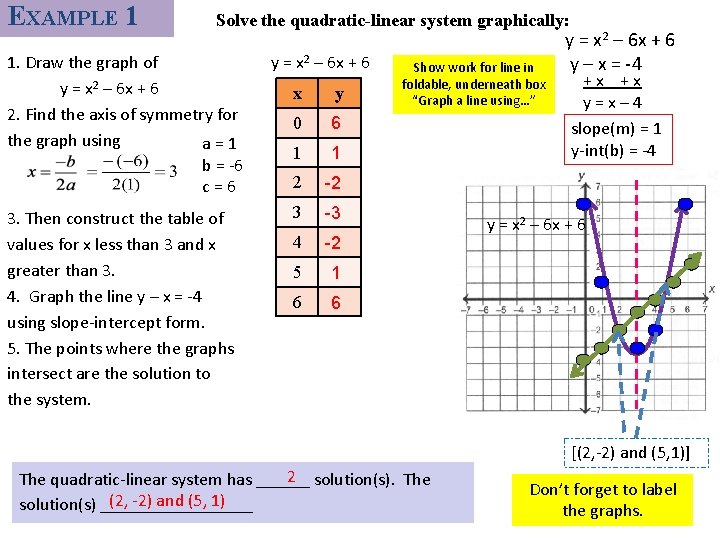
EXAMPLE 1 Solve the quadratic-linear system graphically: 1. Draw the graph of y = x 2 – 6 x + 6 2. Find the axis of symmetry for the graph using a=1 b = -6 c=6 3. Then construct the table of values for x less than 3 and x greater than 3. 4. Graph the line y – x = -4 using slope-intercept form. 5. The points where the graphs intersect are the solution to the system. y = x 2 – 6 x + 6 x y 0 6 1 1 2 -2 3 -3 4 -2 5 1 6 6 Show work for line in foldable, underneath box “Graph a line using…” y = x 2 – 6 x + 6 y – x = -4 +x +x y=x– 4 slope(m) = 1 y-int(b) = -4 y = x 2 – 6 x + 6 [(2, -2) and (5, 1)] 2 solution(s). The quadratic-linear system has ______ (2, -2) and (5, 1) solution(s) _________ Don’t forget to label the graphs.

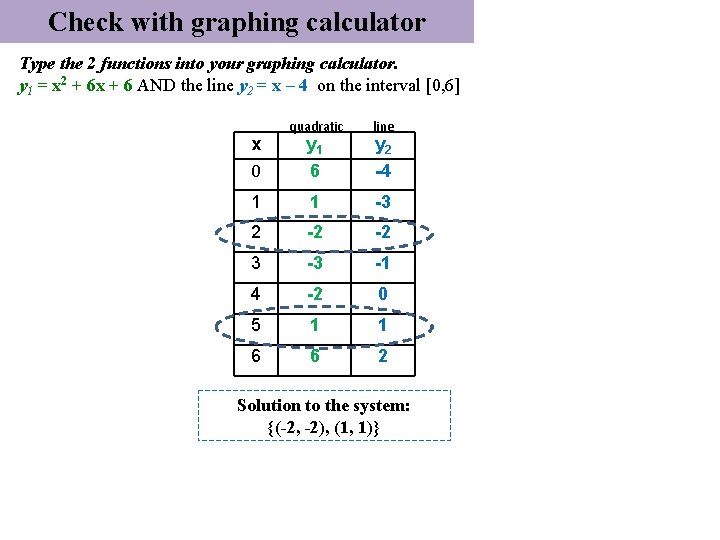
Check with graphing calculator Type the 2 functions into your graphing calculator. y 1 = x 2 + 6 x + 6 AND the line y 2 = x – 4 on the interval [0, 6] quadratic line 0 6 -4 1 1 -3 2 -2 -2 3 -3 -1 4 -2 0 5 1 1 6 6 2 x y 1 y 2 Solution to the system: {(-2, -2), (1, 1)}

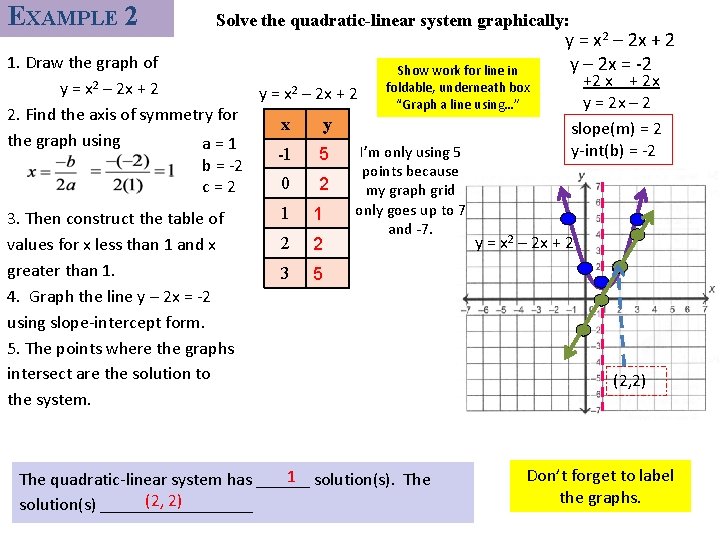
EXAMPLE 2 Solve the quadratic-linear system graphically: 1. Draw the graph of Show work for line in foldable, underneath box y = x 2 – 2 x + 2 “Graph a line using…” 2. Find the axis of symmetry for x y the graph using a=1 I’m only using 5 -1 5 b = -2 points because 0 2 c=2 my graph grid only goes up to 7 1 1 3. Then construct the table of values for x less than 1 and x greater than 1. 4. Graph the line y – 2 x = -2 using slope-intercept form. 5. The points where the graphs intersect are the solution to the system. 2 2 3 5 and -7. 1 solution(s). The quadratic-linear system has ______ (2, 2) solution(s) _________ y = x 2 – 2 x + 2 y – 2 x = -2 +2 x + 2 x y = 2 x – 2 slope(m) = 2 y-int(b) = -2 y = x 2 – 2 x + 2 (2, 2) Don’t forget to label the graphs.

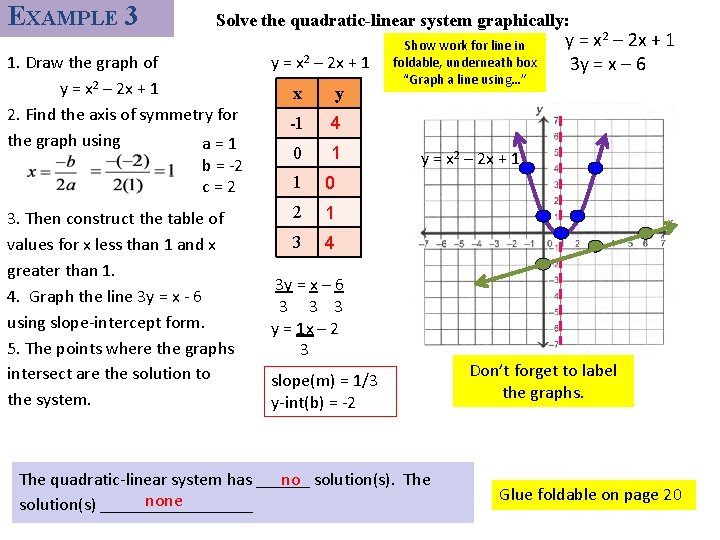
EXAMPLE 3 Solve the quadratic-linear system graphically: 1. Draw the graph of y = x 2 – 2 x + 1 2. Find the axis of symmetry for the graph using a=1 b = -2 c=2 3. Then construct the table of values for x less than 1 and x greater than 1. 4. Graph the line 3 y = x - 6 using slope-intercept form. 5. The points where the graphs intersect are the solution to the system. y = x 2 – 2 x + 1 x y -1 4 0 1 1 0 2 1 3 4 Show work for line in foldable, underneath box “Graph a line using…” y = x 2 – 2 x + 1 3 y = x – 6 3 3 3 y = 1 x – 2 3 slope(m) = 1/3 y-int(b) = -2 no solution(s). The quadratic-linear system has ______ none solution(s) _________ Don’t forget to label the graphs. Glue foldable on page 20

Now in your notebook Pag e 21 Title it: Solving Quadratic-Linear Systems Algebraically 1. Solve: y = x 2 – 6 x + 6 y – x = -4 (x 2 – 6 x + 6) – x = -4 x 2 – 7 x + 6 = -4 +4 +4 x 2 – 7 x + 10 = 0 (x – 5 ) (x – 2) = 0 x=5 x=2 y – x = -4 y – 5 = -4 y – 2 = -4 + 5 +5 + 2 +2 y=1 y = -2 Solution: (5, 1) and (2, -2) Steps: 1. Substitute “x 2 – 6 x + 6” into the linear equation for “y”. 2. Solve for x. 3. Plug the value of x into either equation. ((I’m picking the linear equation) to get y. 4. Check with your calculator. Now look back at #1 in the foldable that you just created. Compare the answers. Yay, they are the same.

Pag 2. Solve: y = x 2 – 2 x + 2 y – 2 x = -2 e 22 (x 2 – 2 x + 2) – 2 x = -2 x 2 – 4 x + 2 = -2 +2 +2 x 2 – 4 x + 4 = 0 Can’t factor a=1 b = -4 c=4 y – 2 x = -2 y – 2(2) = -2 y – 4 = -2 + 4 +4 y=2 Steps: 1. Substitute “x 2 – 2 x + 2” into the linear equation for “y”. 2. Solve for x. 3. Plug the value of x into either equation. ((I’m picking the linear equation) to get y. 4. Check with your calculator. Solution: (2, 2)

Pag 3. Solve: y = x 2 – 2 x + 1 3 y = x – 6 3(x 2 – 2 x + 1) = x – 6 3 x 2 – 6 x + 3 = x – 6 -x +6 3 x 2 – 7 x + 9 = 0 e 23 Can’t factor a=3 b = -7 c=9 Does not work therefore no solution Solution: no solution Steps: 1. Substitute “x 2 – 2 x + 1” into the linear equation for “y”. 2. Solve for x.

• What are three important characteristics of a parabola? • Describe the two ways of finding the roots of a quadratic equation. • What is one way to solve a system with a quadratic and a linear equation?