Chapter 8 Quadratic Functions and Equations Quadratic Function

Chapter 8 Quadratic Functions and Equations

Quadratic. Function A quadratic equation is an equation that can be written as f(x) = ax 2 + bx + c , where a, b, c are real numbers, with a = Axis of symmetry 0. (0, 2) -2 1 (0, 0) Vertex 0 -2 -1 0 -1 1 2 (2, -1) x=2

Vertex Formula The x-coordinate of the vertex of the graph of y = ax 2 +bx +c, a = 0, is given by x = -b/2 a To find the y-coordinate of the vertex, substitute this x-value into the equation

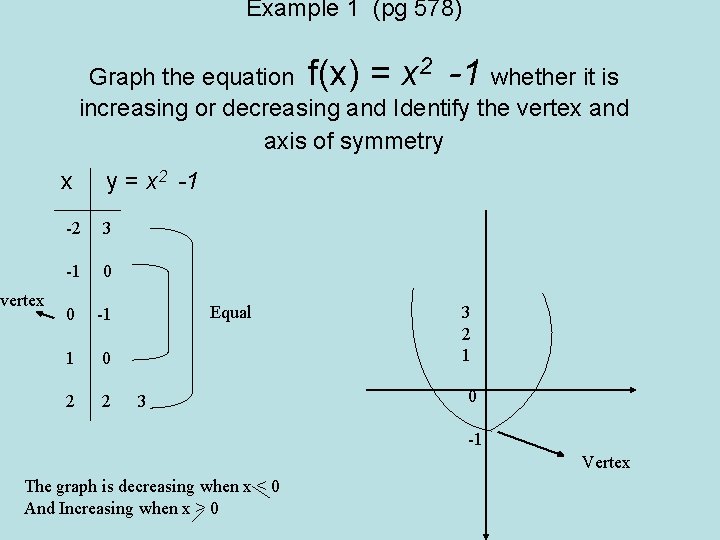
Example 1 (pg 578) Graph the equation f(x) = x 2 -1 whether it is increasing or decreasing and Identify the vertex and axis of symmetry vertex x y = x 2 -1 -2 3 -1 0 0 -1 1 0 2 2 Equal 3 3 2 1 0 -1 Vertex The graph is decreasing when x < 0 And Increasing when x > 0

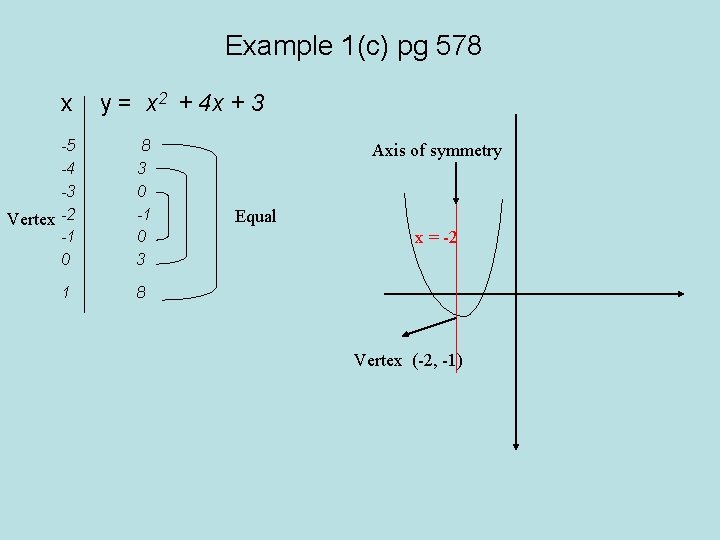
Example 1(c) pg 578 x -5 -4 -3 Vertex -2 -1 0 1 y = x 2 + 4 x + 3 8 3 0 -1 0 3 Axis of symmetry Equal x = -2 8 Vertex (-2, -1)

Find the vertex of a parabola f(x) = 2 x 2 - 4 x + 1 Symbolically f(x) = 2 x 2 – 4 x + 1 a=2 , b=-4 x = -b/2 a = - (-4)/2. 2 = 4/4 = 1 To find the y-value of the vertex, Substitute x = 1 in the given formula f(1) = 2. 12 - 4. 1 + 1= -1 The vertex is (1, -1) Graphically [ -4. 7, 1] , [-3. 1, 1]

Example 7 (Pg 583) Maximizing Revenue The regular price of a hotel room is $ 80, Each room rented the price decreases by $2 900 800 700 600 500 400 (20, 800) Maximum revenue 0 5 10 15 20 25 30 35 40 If x rooms are rented then the price of each room is 80 – 2 x The revenue equals the number of rooms rented times the price of each room. Thus f(x) = x(80 – 2 x) = 80 x - 2 x 2 = -2 x 2 + 80 x The x-coordinate of the vertex x = - b/2 a = - 80/ 2(-2) = 20 Y coordinate f(20) = -2(20)2 + 80 (20) = 800

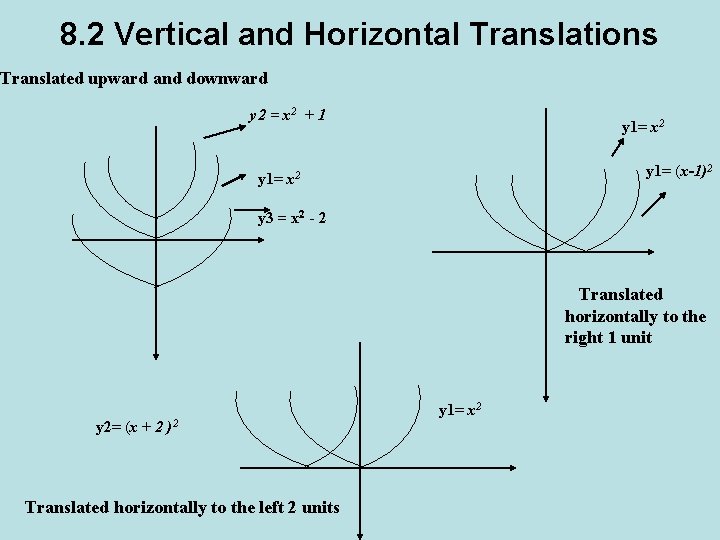
8. 2 Vertical and Horizontal Translations Translated upward and downward y 2 = x 2 + 1 y 1= x 2 y 1= (x-1)2 x 2 y 3 = x 2 - 2 Translated horizontally to the right 1 unit y 2= (x + 2 )2 Translated horizontally to the left 2 units y 1= x 2

Vertical and Horizontal Translations Of Parabolas (pg 591) Let h , k be positive numbers. To graph y = x 2 + k y = x 2 – k y = (x – k)2 y = (x +k)2 shift the graph of y = x 2 by k units upward downward right left

Vertex Form of a Parabola (Pg 592) The vertex form of a parabola with vertex (h, k) is y = a (x – h)2 + k, where a = 0 is a constant. If a > 0, the parabola opens upward; if a < 0, the parabola opens downward.

Ch 8. 3 Quadratic Equations A quadratic equation is an equation that can be written as ax 2 +bx +c= 0, where a, b, c are real numbers with a = 0

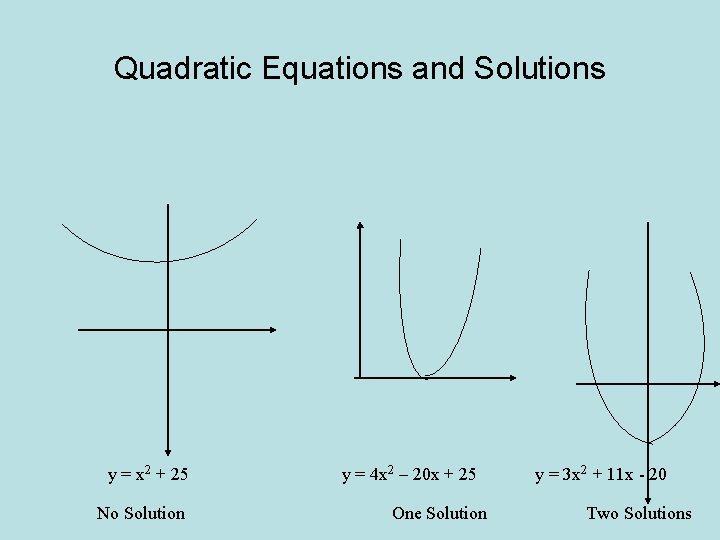
Quadratic Equations and Solutions y = x 2 + 25 No Solution y = 4 x 2 – 20 x + 25 One Solution y = 3 x 2 + 11 x - 20 Two Solutions

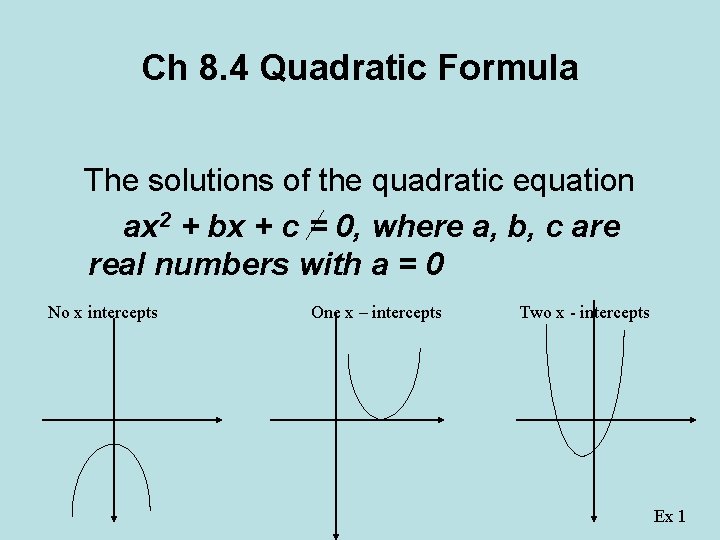
Ch 8. 4 Quadratic Formula The solutions of the quadratic equation ax 2 + bx + c = 0, where a, b, c are real numbers with a = 0 No x intercepts One x – intercepts Two x - intercepts Ex 1

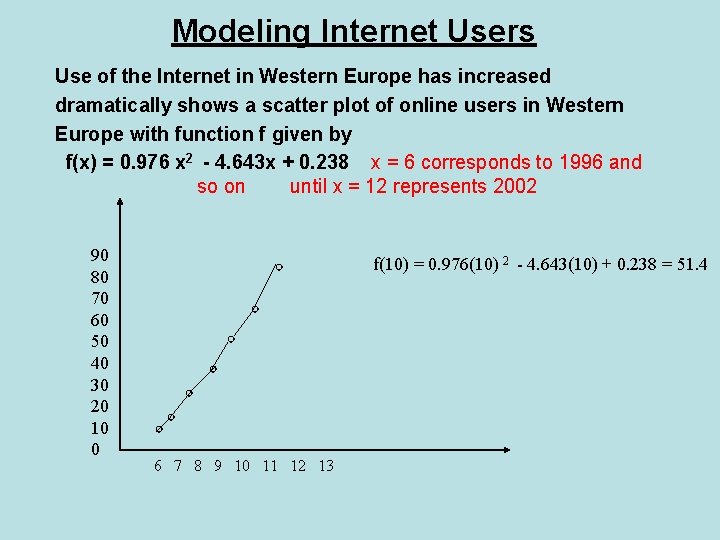
Modeling Internet Users Use of the Internet in Western Europe has increased dramatically shows a scatter plot of online users in Western Europe with function f given by f(x) = 0. 976 x 2 - 4. 643 x + 0. 238 x = 6 corresponds to 1996 and so on until x = 12 represents 2002 90 80 70 60 50 40 30 20 10 0 f(10) = 0. 976(10) 2 - 4. 643(10) + 0. 238 = 51. 4 6 7 8 9 10 11 12 13

8. 4 Quadratic Formula The solutions to ax 2 + bx + c = 0 with a = 0 are given by - b + b 2 – 4 ac X= 2 a

The Discriminant and Quadratic Equation To determine the number of solutions to ax 2 + bx + c = 0 , evaluate the discriminant b If If If 2 2 – 4 ac > 0, b – 4 ac > 0, there are two real solutions 2 b – 4 ac = 0, there is one real solution 2 b – 4 ac < 0, there are no real solutions , but two complex solution