Grade C Graphs of quadratic functions Recognise sketch

Grade C Graphs of quadratic functions Recognise, sketch and interpret graphs of quadratic functions If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key Vocabulary Co-ordinates Function Parabola Plot Quadratic Equation Expression Solve Factorise Substitute

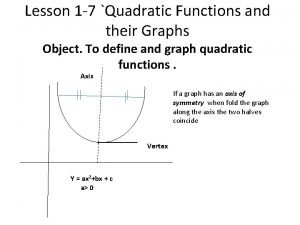
What is a Quadratic Function? Quadratic function is a function that can be described by an equation of the form y = ax 2 + bx + c, where a ≠ 0. The graph of a quadratic function will look like a ‘U’ shape. Note: This shaped graph is called a parabola.

How to recognise Quadratic Functions? Which of these are Quadratic Functions? 1) y = 2 x 2 - 3 x + 7 2) y = 7 x + 6 3) y = x 2 - 7 x 4) y = x 2 5) y = x 3 - 2 x - 7 Hint: y = ax 2 + bx + c

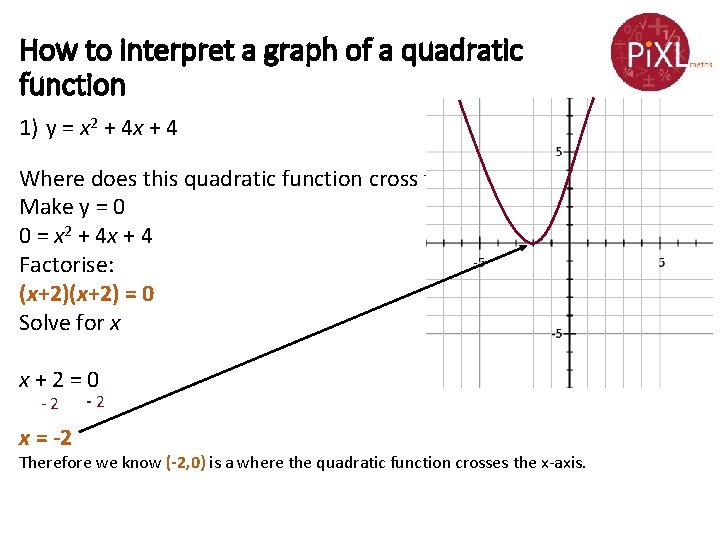
How to interpret a graph of a quadratic function 1) y = x 2 + 4 x + 4 Where does this quadratic function cross the x-axis? Make y = 0 0 = x 2 + 4 x + 4 Factorise: (x+2) = 0 Solve for x x + 2 = 0 - 2 x = -2 - 2 Therefore we know (-2, 0) is a where the quadratic function crosses the x-axis.

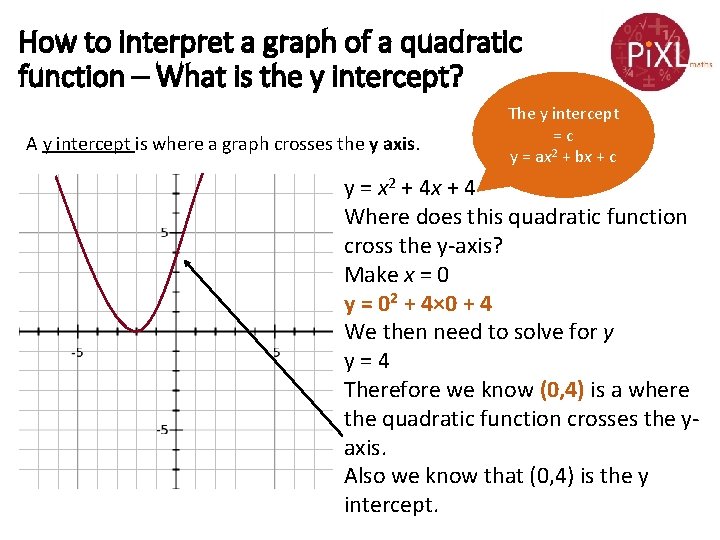
How to interpret a graph of a quadratic function – What is the y intercept? A y intercept is where a graph crosses the y axis. The y intercept = c y = ax 2 + bx + c y = x 2 + 4 x + 4 Where does this quadratic function cross the y-axis? Make x = 0 y = 02 + 4× 0 + 4 We then need to solve for y y = 4 Therefore we know (0, 4) is a where the quadratic function crosses the yaxis. Also we know that (0, 4) is the y intercept.

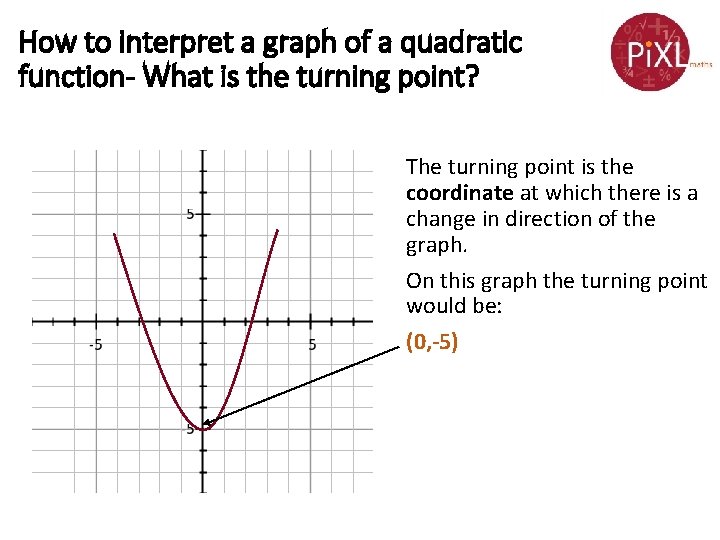
How to interpret a graph of a quadratic function- What is the turning point? The turning point is the coordinate at which there is a change in direction of the graph. On this graph the turning point would be: (0, -5)

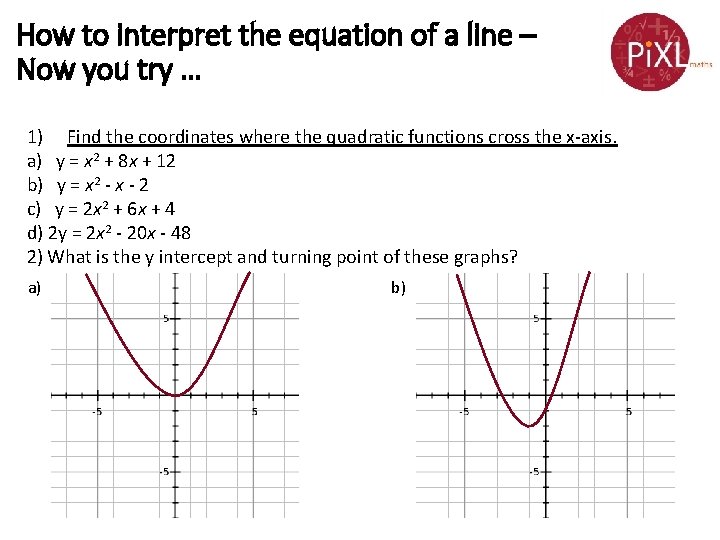
How to interpret the equation of a line – Now you try … 1) Find the coordinates where the quadratic functions cross the x-axis. a) y = x 2 + 8 x + 12 b) y = x 2 - x - 2 c) y = 2 x 2 + 6 x + 4 d) 2 y = 2 x 2 - 20 x - 48 2) What is the y intercept and turning point of these graphs? a) b)

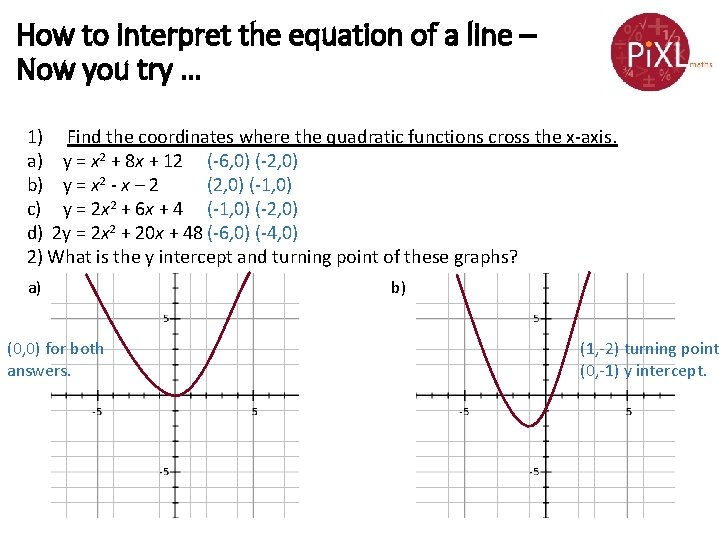
How to interpret the equation of a line – Now you try … 1) Find the coordinates where the quadratic functions cross the x-axis. a) y = x 2 + 8 x + 12 (-6, 0) (-2, 0) b) y = x 2 - x – 2 (2, 0) (-1, 0) c) y = 2 x 2 + 6 x + 4 (-1, 0) (-2, 0) d) 2 y = 2 x 2 + 20 x + 48 (-6, 0) (-4, 0) 2) What is the y intercept and turning point of these graphs? a) (0, 0) for both answers. b) (1, -2) turning point (0, -1) y intercept.

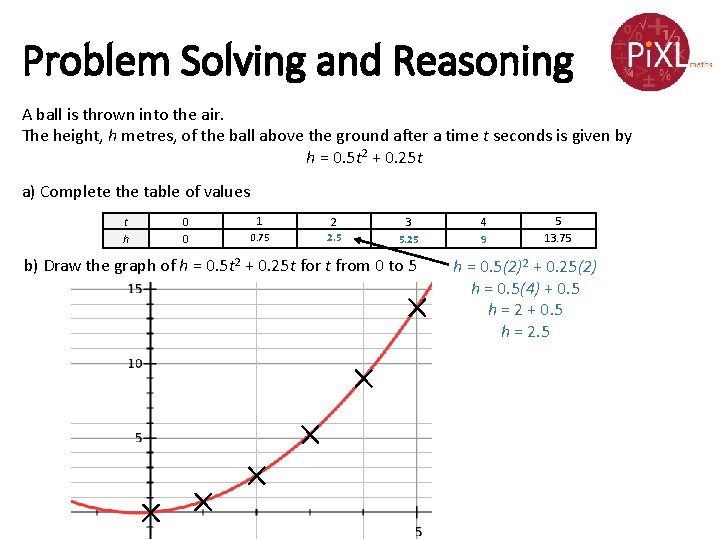
Problem Solving and Reasoning A ball is thrown into the air. The height, h metres, of the ball above the ground after a time t seconds is given by h = 0. 5 t 2 + 0. 25 t a) Complete the table of values t h 0 0 1 2 0. 75 b) Draw the graph of h = 0. 5 t 2 + 0. 25 t for t from 0 to 5 3 4 5 13. 75

Problem Solving and Reasoning A ball is thrown into the air. The height, h metres, of the ball above the ground after a time t seconds is given by h = 0. 5 t 2 + 0. 25 t a) Complete the table of values t h 0 0 1 2 3 4 0. 75 2. 5 5. 25 9 b) Draw the graph of h = 0. 5 t 2 + 0. 25 t for t from 0 to 5 5 13. 75 h = 0. 5(2)2 + 0. 25(2) h = 0. 5(4) + 0. 5 h = 2. 5

Reason and explain § What will the quadratic function graph look like if the coefficient of x 2 was to be negative? E. G y = -x 2 + 2 x + 1 § What does this quadratic function, y = 2 x 2 + 5 x, suggest about the graphically? § What does this quadratic function, y = x 2 + 6 x + 9, suggest about the graphically? Hint: Think about the number of solutions there are for x