Algebra 9 3 Graphing Quadratic Functions CLASSIFYING EQUATIONS

Algebra 9. 3 Graphing Quadratic Functions

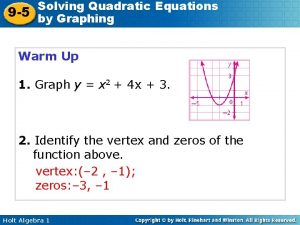
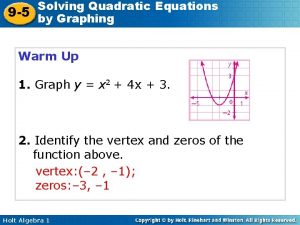
CLASSIFYING EQUATIONS yy == 2 x²+ 2 x + 47 x + 3 What isyythe == 5 x² 5 x pattern ? yy == x² x --44 LINEAR QUADRATIC

Standard Form of a Quadratic Equation y = ax²+ bx + c (a ≠ 0) An equation is called QUADRATIC if it has a squared variable There MUST be a squared variable. There may or may not be the “middle term” or the constant.

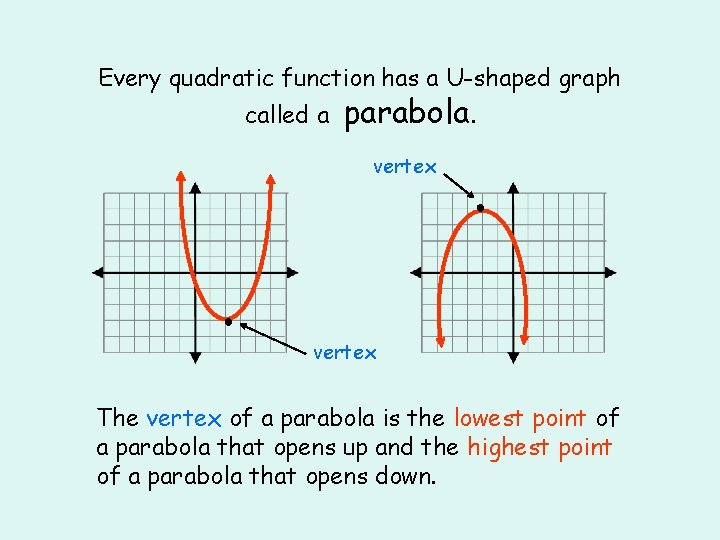
Every quadratic function has a U-shaped graph called a parabola. vertex ● ● vertex The vertex of a parabola is the lowest point of a parabola that opens up and the highest point of a parabola that opens down.

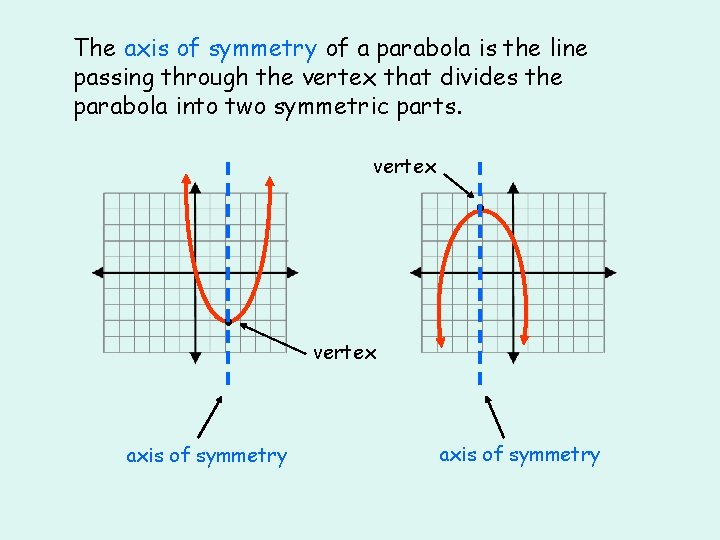
The axis of symmetry of a parabola is the line passing through the vertex that divides the parabola into two symmetric parts. vertex ● ● vertex axis of symmetry

Identifying a, b and c y = ax²+ bx + c (a ≠ 0) In y = 2 x²+ 3 x – 5 a= 2 b= 3 c = -5 In y = -x²- 5 x + 2 a = -1 b = -5 c = 2 In y = x²- 3 x a= 1 In y = -x²+ 4 a = -1 b = 0 c= 4 In y = -3 x² a = -3 b = 0 c= 0 b = -3 c = 0

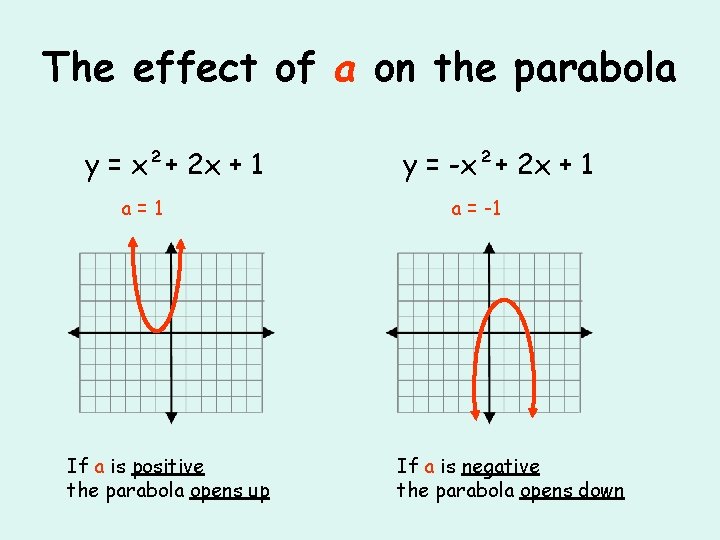
The effect of a on the parabola y = x²+ 2 x + 1 a=1 If a is positive the parabola opens up y = -x²+ 2 x + 1 a = -1 If a is negative the parabola opens down

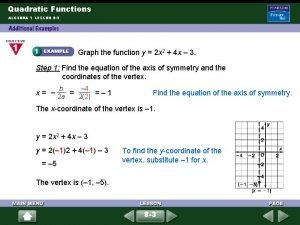
Finding the vertex ● In the equation y = ax²+ bx + c the x coordinate of the vertex can be found using the formula: Then substitute the x value into the original equation to find the y coordinate In y = x²+ 4 x + 8 VERTEX: x = a= 1 b= 4 c= 8 y = (-2)² + 4(-2) + 8 y = 4 -8 + 8 = 4 VERTEX: (-2, 4)

Graphing a Quadratic Function STEPS 1. Find the x coordinate of the vertex: x= Draw the line of symmetry at the x-value. Then substitute the x value to find y. The vertex will be an ordered pair (x, y). 2. Make an x/y table. Choose x values to the left and right of the vertex. Plot as you go. 3. 3. Connect the points as a smooth curve.

Graph: y = x²- 2 x - 3 Vertex: x = = y =1 y = (1)² - 2(1) – 3 = -4 x y -1 0 0 -3 1 -4 2 -3 3 0 ● ● ● x

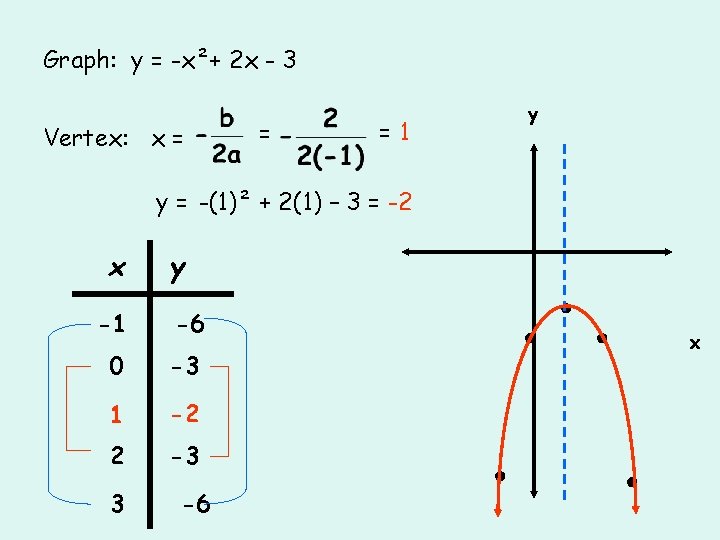
Graph: y = -x²+ 2 x - 3 Vertex: x = = y =1 y = -(1)² + 2(1) – 3 = -2 x y -1 -6 0 -3 1 -2 2 -3 3 -6 ● ● x ●

A Few together from the Homework pg. 521 # 5 and #15

Homework pg. 521 # 1 -15