Solving Quadratic Equations 9 5 by Graphing Warm

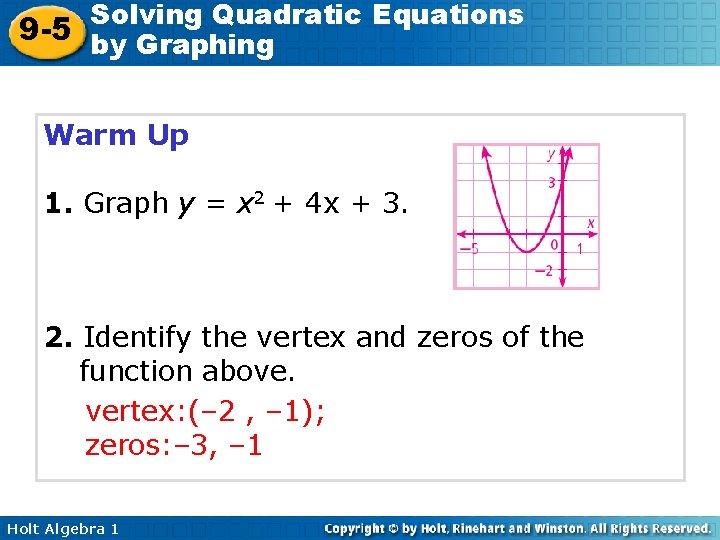
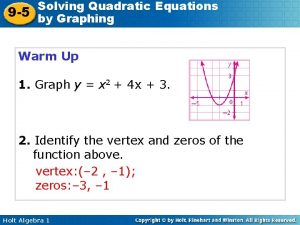
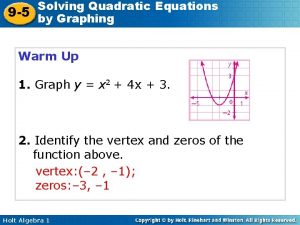
Solving Quadratic Equations 9 -5 by Graphing Warm Up 1. Graph y = x 2 + 4 x + 3. 2. Identify the vertex and zeros of the function above. vertex: (– 2 , – 1); zeros: – 3, – 1 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Learning Target Students will be able to: Solve quadratic equations by graphing. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Every quadratic function has a related quadratic equation. A quadratic equation is an equation that can be written in the standard form ax 2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax 2 + bx + c 0 = ax 2 + bx + c = 0 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing One way to solve a quadratic equation in standard form is to graph the related function and find the x -values where y = 0. In other words, find the zeros of the related function. Recall that a quadratic function may have two, one, or no zeros. Holt Algebra 1

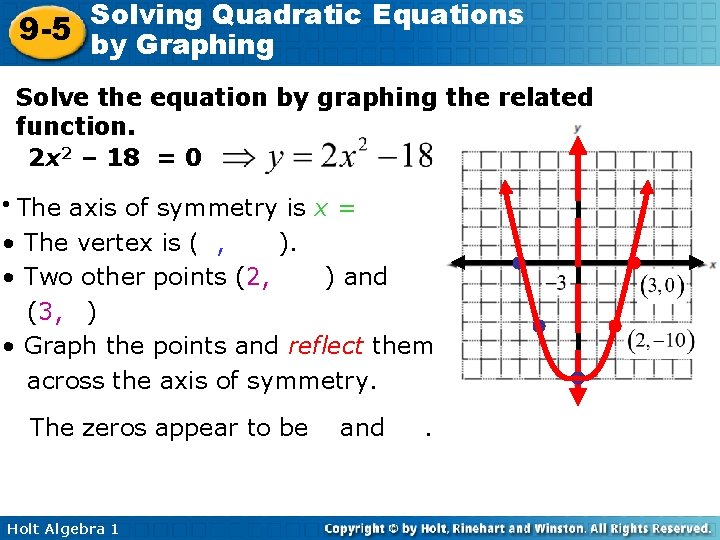
Solving Quadratic Equations 9 -5 by Graphing Solve the equation by graphing the related function. 2 x 2 – 18 = 0 The axis of symmetry is x = 0. • The vertex is (0, – 18). • Two other points (2, – 10) and (3, 0) • Graph the points and reflect them across the axis of symmetry. • The zeros appear to be 3 and – 3. Holt Algebra 1

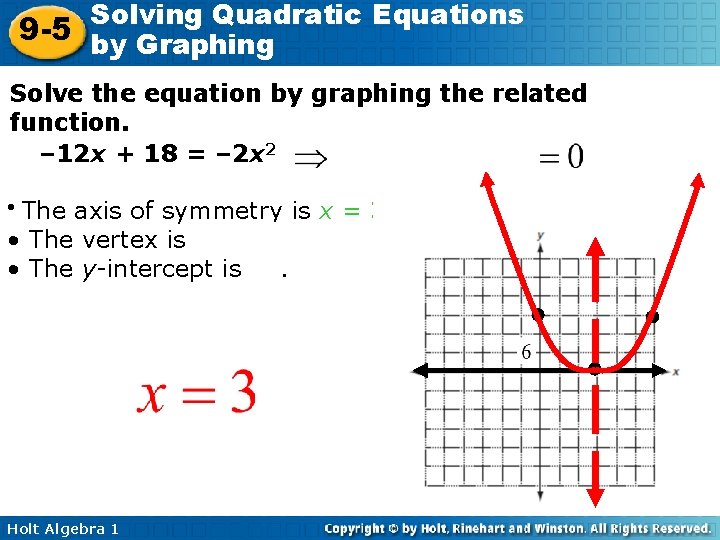
Solving Quadratic Equations 9 -5 by Graphing Solve the equation by graphing the related function. – 12 x + 18 = – 2 x 2 The axis of symmetry is x = 3. • The vertex is (3, 0). • The y-intercept is 18. • Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Solve the equation by graphing the related function. x 2 – 8 x – 16 = 2 x 2 The axis of symmetry is x = – 4. • The vertex is (– 4, 0). • The y-intercept is 16. • Two other points are (– 3, 1) and (– 2, 4). • Graph the points and reflect them across the axis of symmetry. • The only zero appears to be – 4. Holt Algebra 1

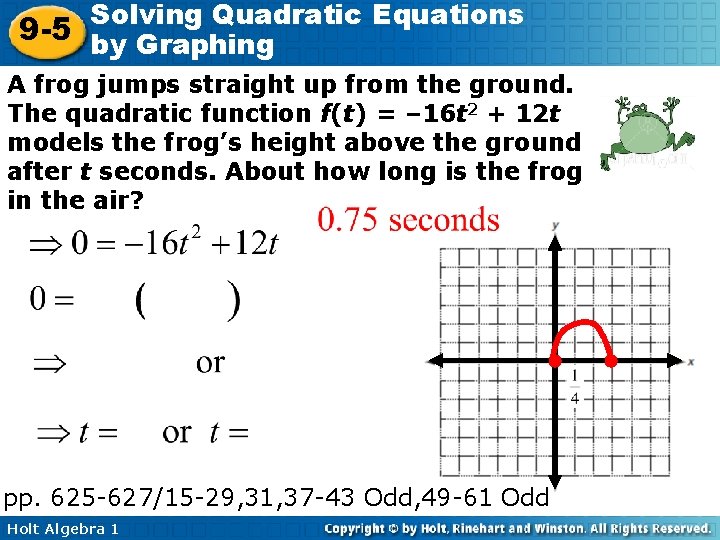
Solving Quadratic Equations 9 -5 by Graphing A frog jumps straight up from the ground. The quadratic function f(t) = – 16 t 2 + 12 t models the frog’s height above the ground after t seconds. About how long is the frog in the air? pp. 625 -627/15 -29, 31, 37 -43 Odd, 49 -61 Odd Holt Algebra 1