Solving Quadratic Equations 9 5 by Graphing Warm

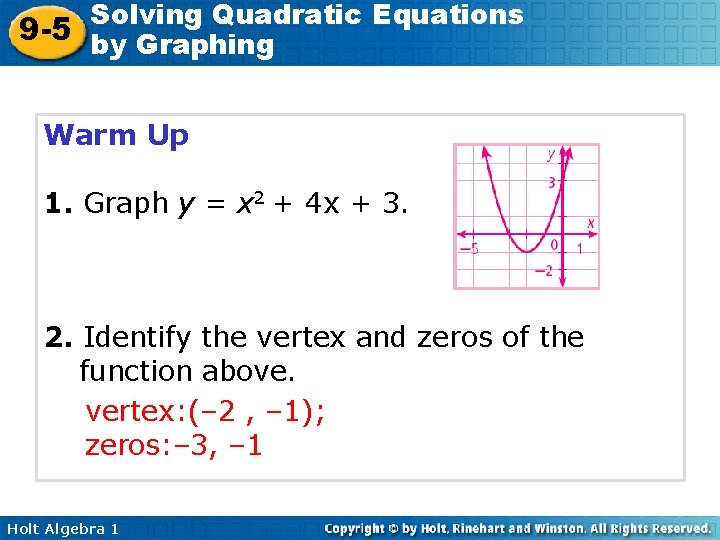
Solving Quadratic Equations 9 -5 by Graphing Warm Up 1. Graph y = x 2 + 4 x + 3. 2. Identify the vertex and zeros of the function above. vertex: (– 2 , – 1); zeros: – 3, – 1 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing 9 -5 Solving Quadratic Equations by Graphing Holt Algebra 11

Solving Quadratic Equations 9 -5 by Graphing A quadratic equation is an equation that can be written in the standard form ax 2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax 2 + bx + c 0 = ax 2 + bx + c = 0 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 1 A: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. 2 x 2 – 18 = 0 Step 1 Write the related function. 2 x 2 – 18 = y, or y = 2 x 2 + 0 x – 18 Step 2 Graph the function. The axis of symmetry is x = 0. • The vertex is (0, – 18). • Two other points (2, – 10) and (3, 0) • Graph the points and reflect them across the axis of symmetry. • Holt Algebra 1 x=0 ● ● (3, 0) ● ● (2, – 10) ● (0, – 18)

Solving Quadratic Equations 9 -5 by Graphing Example 1 A Continued Solve the equation by graphing the related function. 2 x 2 – 18 = 0 Step 3 Find the zeros. The zeros appear to be 3 and – 3. Check 2 x 2 – 18 = 0 2(3)2 – 18 2(9) – 18 18 – 18 0 Holt Algebra 1 2 x 2 – 18 = 0 0 2(– 3)2 – 18 0 0 Substitute 3 and – 3 2(9) – 18 0 0 for x in the quadratic 18 – 18 0 0 equation.

Solving Quadratic Equations 9 -5 by Graphing Example 1 B: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. – 12 x + 18 = – 2 x 2 Step 1 Write the related function. y = – 2 x 2 + 12 x – 18 x=3 Step 2 Graph the function. The axis of symmetry is x = 3. • The vertex is (3, 0). • Two other points (5, – 8) and (4, – 2). • Graph the points and reflect them across the axis of symmetry. ● • Holt Algebra 1 ● ● ● (3, 0) ● (4, – 2) ● (5, – 8)

Solving Quadratic Equations 9 -5 by Graphing Example 1 B Continued Solve the equation by graphing the related function. – 12 x + 18 = – 2 x 2 Step 3 Find the zeros. The only zero appears to be 3. Check y = – 2 x 2 + 12 x – 18 0 – 2(3)2 + 12(3) – 18 0 – 18 + 36 – 18 0 0 You can also confirm the solution by using the Table function. Enter the function and press When y = 0, x = 3. The x-intercept is 3. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 a Continued Solve the equation by graphing the related function. x 2 – 8 x – 16 = 2 x 2 Step 3 Find the zeros. The only zero appears to be – 4. Check Holt Algebra 1 y = x 2 + 8 x + 16 0 (– 4)2 + 8(– 4) + 16 0 16 – 32 + 16 0 0

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 c Solve the equation by graphing the related function. –x 2 + 4 = 0 Step 1 Write the related function. y = –x 2 + 4 Step 2 Graph the function. Use a graphing calculator. Step 3 Find the zeros. The function appears to have zeros at (2, 0) and (– 2, 0). Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 c Continued Solve the equation by graphing the related function. –x 2 + 4 = 0 The equation has two real-number solutions. Check reasonableness Use the table function. There are two zeros in the Y 1 column. The function appears to have zeros at – 2 and 2. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2: Application A frog jumps straight up from the ground. The quadratic function f(t) = – 16 t 2 + 12 t models the frog’s height above the ground after t seconds. About how long is the frog in the air? When the frog leaves the ground, its height is 0, and when the frog lands, its height is 0. So solve 0 = – 16 t 2 + 12 t to find the times when the frog leaves the ground and lands. Step 1 Write the related function 0 = – 16 t 2 + 12 t y = – 16 t 2 + 12 t Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2 Continued Step 2 Graph the function. Use a graphing calculator. Step 3 Use to estimate the zeros. The zeros appear to be 0 and 0. 75. The frog leaves the ground at 0 seconds and lands at 0. 75 seconds. The frog is off the ground for about 0. 75 seconds. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2 Continued Check 0 = 0 0 Holt Algebra 1 – 16 t 2 + 12 t – 16(0. 75)2 + 12(0. 75) – 16(0. 5625) + 9 – 9 + 9 0 Substitute 0. 75 for x in the quadratic equation.

Solving Quadratic Equations 9 -5 by Graphing Lesson Quiz Solve each equation by graphing the related function. 1. 3 x 2 – 12 = 0 2, – 2 2. x 2 + 2 x = 8 – 4, 2 3. 3 x – 5 = x 2 no solution 4. 3 x 2 + 3 = 6 x 1 5. A rocket is shot straight up from the ground. The quadratic function f(t) = – 16 t 2 + 96 t models the rocket’s height above the ground after t seconds. How long does it take for the rocket to return to the ground. 6 s Holt Algebra 1