9 2 Solving Quadratic Equations by Graphing Algebra

9 -2 Solving Quadratic Equations by Graphing Algebra 1 Glencoe Mc. Graw-Hill Linda Stamper and Jo. Ann Evans

Factoring can be used to determine whether the graph of a quadratic functions intersects the x-axis in one or two points. The graph intersects the x-axis when f(x) equals 0. function Factor. Identify the roots. related equation – 12 4 – 3 1 The graph of the function intersects the x-axis two times.

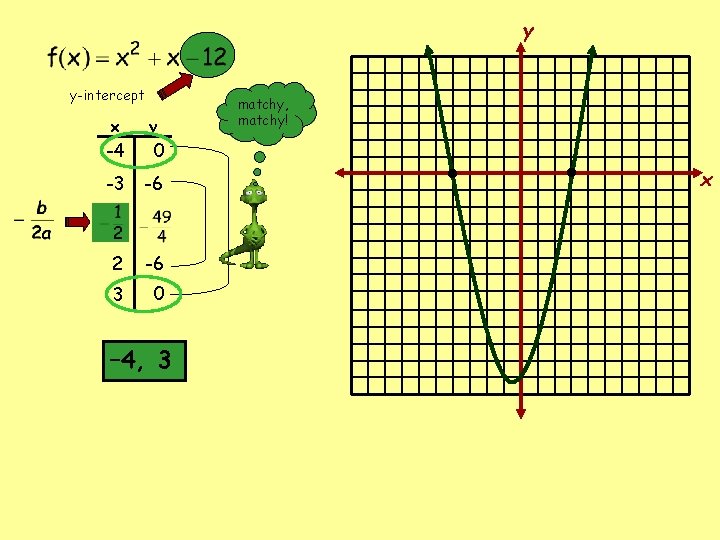
y y-intercept x y -4 0 -3 -6 2 -6 3 0 – 4, 3 matchy, matchy! • • x

Use factoring to determine how many times the graph of each function intersects the x-axis. Identify each root. Remember: The graph intersects the x-axis when f(x) equals 0. Example 1 Two roots; -5, 2 Example 2 One root; 5 Example 3 Two roots; -1, Example 4 Two roots; -11,

In previous graphing to find solutions, the roots of the equations were integers. Usually the roots of a quadratic equation are not integers. In these cases, use estimation to approximate the roots of the equation. Solve x 2 + 6 x + 7 by graphing. If integral roots cannot be found, estimate the roots by stating the consecutive integers between which the roots lie. Integral roots are roots that are integers (positive and negative whole numbers).

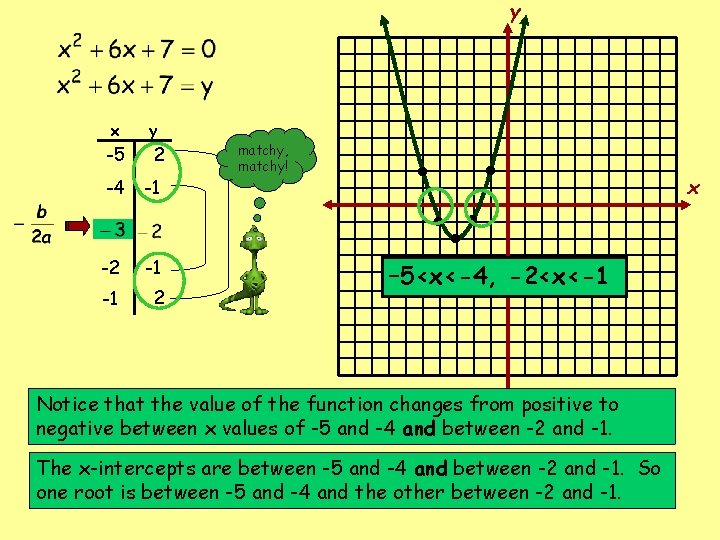
y x y -5 2 -4 -1 -2 -1 -1 2 matchy, matchy! • • • • • – 5<x<-4, -2<x<-1 Notice that the value of the function changes from positive to negative between x values of -5 and -4 and between -2 and -1. The x-intercepts are between -5 and -4 and between -2 and -1. So one root is between -5 and -4 and the other between -2 and -1. x

Solve by graphing. If integral roots cannot be found, estimate the roots by stating the consecutive integers between which the roots lie. Example 5 Example 6 Example 7 Example 8 Example 9

Example 5 x y 0 -3 -1 matchy, matchy! -7 -1. 5 -7. 5 -2 -7 -3 -3 – 4 < x < -3, 0 < x < 1

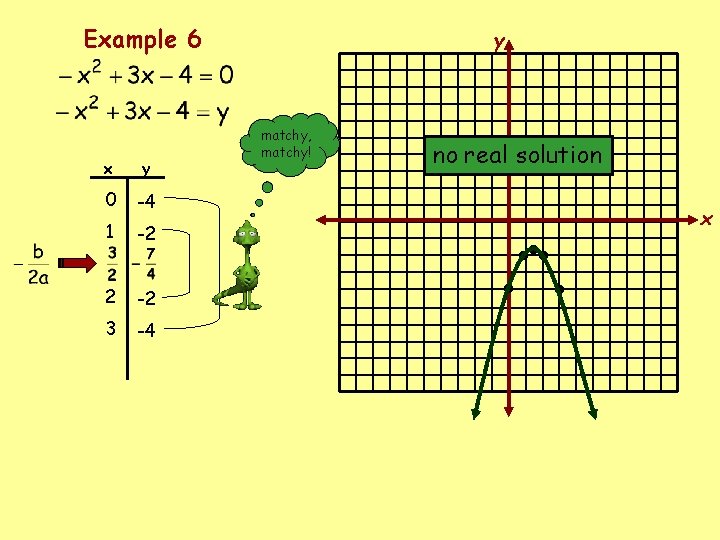
Example 6 x y 0 -4 1 -2 2 -2 3 -4 y matchy, matchy! no real solution • • • • • x

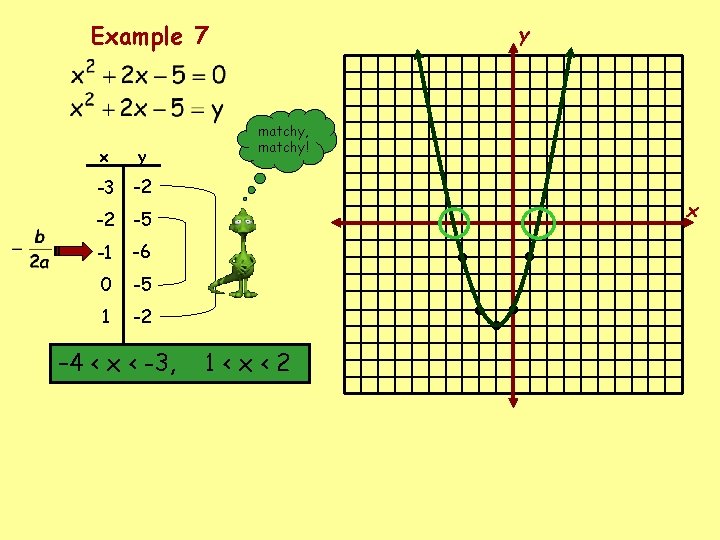
Example 7 x y -3 -2 -2 -5 -1 -6 0 -5 1 -2 – 4 < x < -3, y matchy, matchy! 1<x<2 • • • • • x

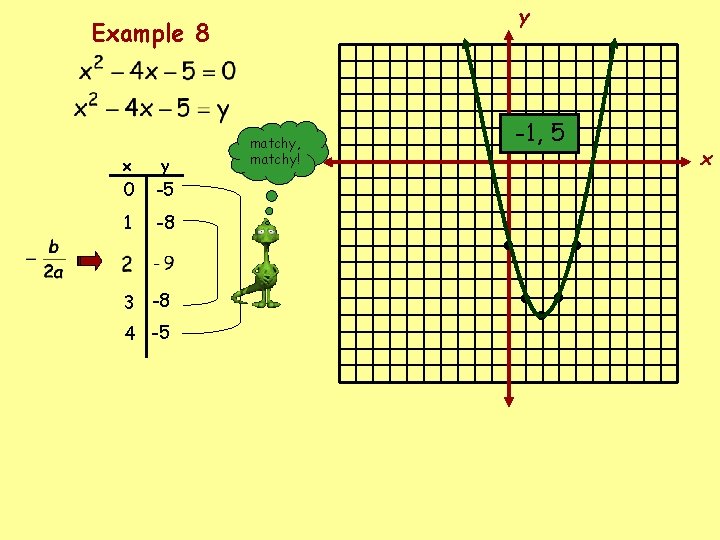
y Example 8 x y 0 -5 1 -8 3 -8 4 -5 matchy, matchy! -1, 5 • • • • • x

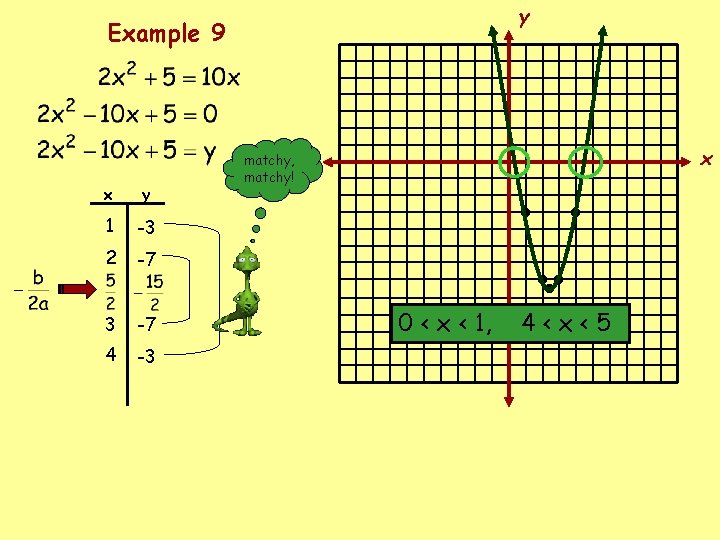
y Example 9 x y 1 -3 2 -7 3 -7 4 -3 x matchy, matchy! 0 < x < 1, • • • • • 4<x<5

Solve by graphing. If integral roots cannot be found, estimate the roots by stating the consecutive integers between which the roots lie. Example 5 – 4 < x < -3, 0 < x < 1 Example 6 no real solution Example 7 – 5 < x < -4, 1 < x < 2 Example 8 -1, 5 Example 9 0 < x < 1, 4 < x < 5

9 -A 4 Handout A 4. All graphs must be completed on graph paper – check out the LCMS website to download coordinate planes.