SOLVING QUADRATIC EQUATIONS GRAPH ICALLY SOLVING QUADRATIC EQUATIONS

Checking a Solution Using a Graph Solve 1 2 x = 8 algebraically. 2

Checking a Solution Using a Graph CHECK Check these solutions using a graph. 1

Checking a Solution Using a Graph CHECK Check these solutions using a graph. 2

Solving an Equation Graphically Solve x 2 – x = 2 graphically. Check your

Solving an Equation Graphically 2 Write the related function y = ax 2 +

Solving an Equation Graphically From the graph, the x-intercepts appear to be x =

USING QUADRATIC MODELS IN REAL LIFE Comparing Two Quadratic Models A shot put champion

Comparing Two Quadratic Models SOLUTION Begin by graphing both models in the same coordinate

Comparing Two Quadratic Models PARABOLIC MOTION An angle of 45 º produces the maximum

Slides: 10

Download presentation

SOLVING QUADRATIC EQUATIONS GRAPH ICALLY SOLVING QUADRATIC EQUATIONS USING GRAPHS The solution of a quadratic equation in one variable x can be solved or checked graphically with the following steps: STEP 1 Write the equation in the form ax 2 + bx + c = 0. STEP 2 Write the related function y = ax 2 + bx + c. STEP 3 Sketch the graph of the function y = ax 2 + bx + c. The solutions, or roots, of ax 2 + bx + c = 0 are the x-intercepts.

Checking a Solution Using a Graph Solve 1 2 x = 8 algebraically. 2 Check your solution graphically. SOLUTION 1 2 x = 8 2 CHECK Write original equation. x 2 = 16 Multiply each side by 2. x= 4 Find the square root of each side. Check these solutions using a graph.

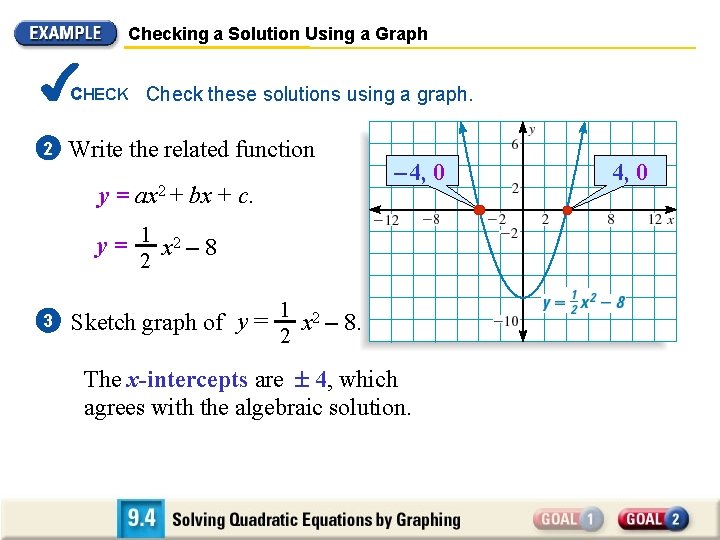
Checking a Solution Using a Graph CHECK Check these solutions using a graph. 1 Write the equation in the form ax 2 + bx + c = 0 1 2 x =8 2 1 2 x – 8=0 2 2 Rewrite original equation. Subtract 8 from both sides. Write the related function y = ax 2 + bx + c. y = 1 x 2 – 8 2

Checking a Solution Using a Graph CHECK Check these solutions using a graph. 2 Write the related function y = ax 2 + bx + c. – 4, 0 y = 1 x 2 – 8 2 3 1 Sketch graph of y = x 2 – 8. 2 The x-intercepts are 4, which agrees with the algebraic solution. 4, 0

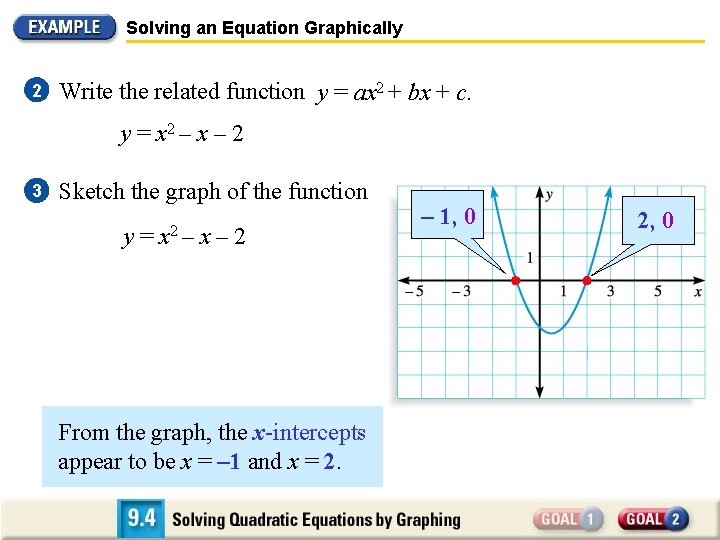
Solving an Equation Graphically Solve x 2 – x = 2 graphically. Check your solution algebraically. SOLUTION 1 Write the equation in the form ax 2 + bx + c = 0 x 2 – x = 2 x 2 – x – 2 = 0 2 Write original equation. Subtract 2 from each side. Write the related function y = ax 2 + bx + c. y = x 2 – x – 2

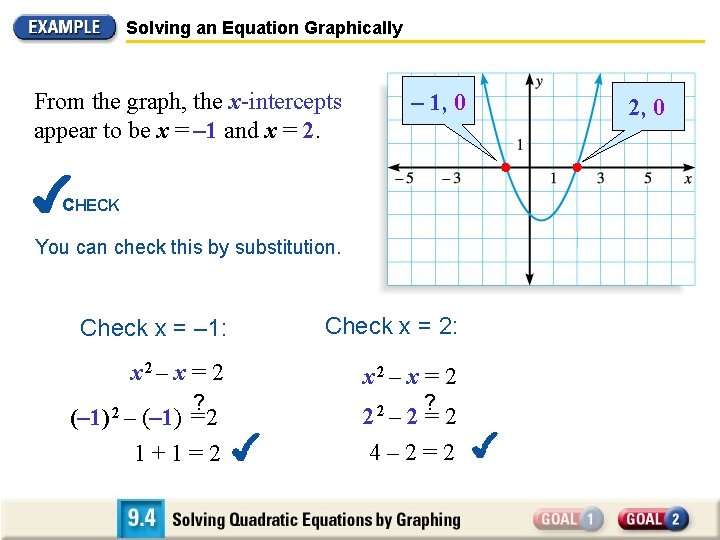
Solving an Equation Graphically 2 Write the related function y = ax 2 + bx + c. y = x 2 – x – 2 3 Sketch the graph of the function y = x 2 – x – 2 From the graph, the x-intercepts appear to be x = – 1 and x = 2. – 1, 0 2, 0

Solving an Equation Graphically From the graph, the x-intercepts appear to be x = – 1 and x = 2. – 1, 0 CHECK You can check this by substitution. Check x = – 1: Check x = 2: x 2 – x = 2 ? ? (– 1) = 2 22 – 2 = 2 1+1=2 4– 2=2 (– 1) 2 – 2, 0

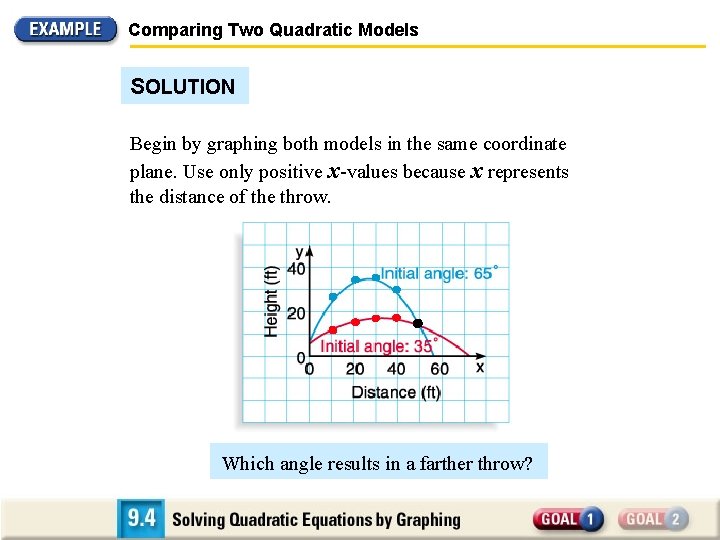
USING QUADRATIC MODELS IN REAL LIFE Comparing Two Quadratic Models A shot put champion performs an experiment for your math class. Assume that both times he releases the shot with the same initial speed but at different angles. The path of each put can be modeled by one of the equations below, where x represents the horizontal distance (in feet) and y represents the height (in feet). Initial angle of 35º: y = – 0. 010735 x 2 + 0. 700208 x + 6 Initial angle of 65º: y = – 0. 040330 x 2 + 2. 144507 x + 6 Which angle results in a farther throw?

Comparing Two Quadratic Models SOLUTION Begin by graphing both models in the same coordinate plane. Use only positive x-values because x represents the distance of the throw. Which angle results in a farther throw?

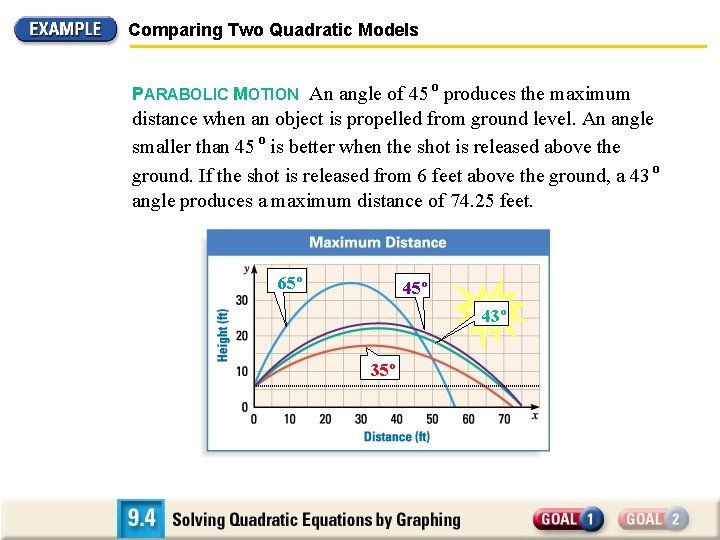
Comparing Two Quadratic Models PARABOLIC MOTION An angle of 45 º produces the maximum distance when an object is propelled from ground level. An angle smaller than 45 º is better when the shot is released above the ground. If the shot is released from 6 feet above the ground, a 43 º angle produces a maximum distance of 74. 25 feet. 65º 43º 35º