Solving Quadratic Equations 9 5 byby Graphing Warm

Solving Quadratic Equations 9 -5 byby Graphing Warm Up Lesson Presentation Lesson Quiz Holt Algebra 11

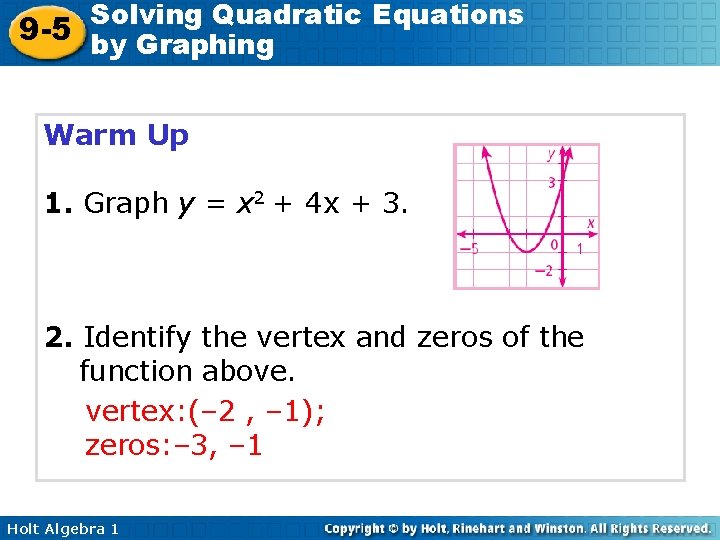
Solving Quadratic Equations 9 -5 by Graphing Warm Up 1. Graph y = x 2 + 4 x + 3. 2. Identify the vertex and zeros of the function above. vertex: (– 2 , – 1); zeros: – 3, – 1 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Objective Solve quadratic equations by graphing. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Vocabulary quadratic equation Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Every quadratic function has a related quadratic equation. A quadratic equation is an equation that can be written in the standard form ax 2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax 2 + bx + c 0 = ax 2 + bx + c = 0 Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing One way to solve a quadratic equation in standard form is to graph the related function and find the x -values where y = 0. In other words, fine the zeros of the related function. Recall that a quadratic function may have two, one, or no zeros. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 1 A: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. 2 x 2 – 18 = 0 Step 1 Write the related function. 2 x 2 – 18 = y, or y = 2 x 2 + 0 x – 18 Step 2 Graph the function. The axis of symmetry is x = 0. • The vertex is (0, – 18). • Two other points (2, – 10) and (3, 0) • Graph the points and reflect them across the axis of symmetry. • Holt Algebra 1 x=0 ● ● (3, 0) ● ● (2, – 10) ● (0, – 18)

Solving Quadratic Equations 9 -5 by Graphing Example 1 A Continued Solve the equation by graphing the related function. 2 x 2 – 18 = 0 Step 3 Find the zeros. The zeros appear to be 3 and – 3. Check 2 x 2 – 18 = 0 2(3)2 – 18 2(9) – 18 18 – 18 0 Holt Algebra 1 2 x 2 – 18 = 0 0 2(– 3)2 – 18 0 0 Substitute 3 and – 3 2(9) – 18 0 0 for x in the quadratic 18 – 18 0 0 equation.

Solving Quadratic Equations 9 -5 by Graphing Example 1 B: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. – 12 x + 18 = – 2 x 2 Step 1 Write the related function. y = – 2 x 2 + 12 x – 18 x=3 Step 2 Graph the function. The axis of symmetry is x = 3. • The vertex is (3, 0). • Two other points (5, – 8) and (4, – 2). • Graph the points and reflect them across the axis of symmetry. ● • Holt Algebra 1 ● ● ● (3, 0) ● (4, – 2) ● (5, – 8)

Solving Quadratic Equations 9 -5 by Graphing Example 1 B Continued Solve the equation by graphing the related function. – 12 x + 18 = – 2 x 2 Step 3 Find the zeros. The only zero appears to be 3. Check y = – 2 x 2 + 12 x – 18 0 – 2(3)2 + 12(3) – 18 0 – 18 + 36 – 18 0 0 You can also confirm the solution by using the Table function. Enter the function and press When y = 0, x = 3. The x-intercept is 3. Holt Algebra 1

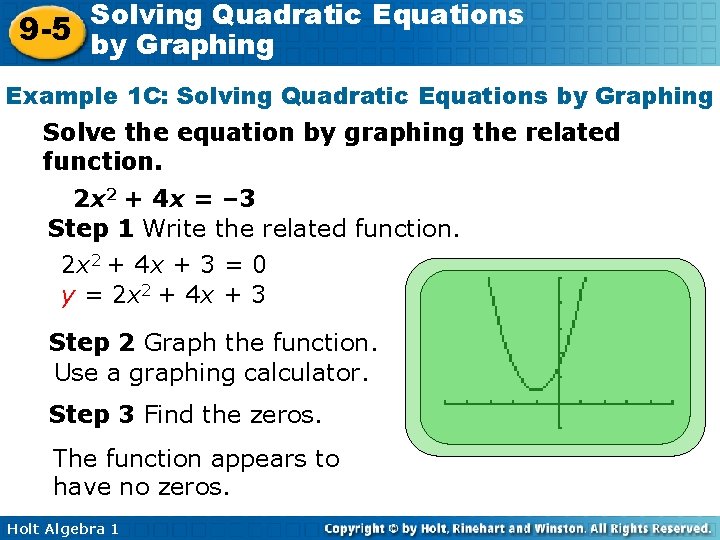
Solving Quadratic Equations 9 -5 by Graphing Example 1 C: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. 2 x 2 + 4 x = – 3 Step 1 Write the related function. 2 x 2 + 4 x + 3 = 0 y = 2 x 2 + 4 x + 3 Step 2 Graph the function. Use a graphing calculator. Step 3 Find the zeros. The function appears to have no zeros. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 1 C: Solving Quadratic Equations by Graphing Solve the equation by graphing the related function. 2 x 2 + 4 x = – 3 The equation has no real-number solutions. Check reasonableness Use the table function. There are no zeros in the Y 1 column. Also, the signs of the values in this column do not change. The function appears to have no zeros. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 a Solve the equation by graphing the related function. x 2 – 8 x – 16 = 2 x 2 Step 1 Write the related function. y = x 2 + 8 x + 16 Step 2 Graph the function. • The axis of symmetry is x = – 4. • The vertex is (– 4, 0). • The y-intercept is 16. • Two other points are (– 3, 1) and (– 2, 4). • Graph the points and reflect them across the axis of symmetry. Holt Algebra 1 x = – 4 ●(– 2 , 4) ● ● (– 3, 1) (– 4, 0)

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 a Continued Solve the equation by graphing the related function. x 2 – 8 x – 16 = 2 x 2 Step 3 Find the zeros. The only zero appears to be – 4. Check Holt Algebra 1 y = x 2 + 8 x + 16 0 (– 4)2 + 8(– 4) + 16 0 16 – 32 + 16 0 0

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 b Solve the equation by graphing the related function. 6 x + 10 = –x 2 Step 1 Write the related function. y = x 2 + 6 x + 10 Step 2 Graph the function. • The axis of symmetry is x = – 3. • The vertex is (– 3 , 1). • The y-intercept is 10. • Two other points (– 1, 5) and (– 2, 2) • Graph the points and reflect them across the axis of symmetry. Holt Algebra 1 x = – 3 ● (– 1, 5) ● ● (– 2, 2) (– 3, 1)

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 b Continued Solve the equation by graphing the related function. 6 x + 10 = –x 2 Step 3 Find the zeros. There appears to be no zeros. You can confirm the solution by using the Table function. Enter the function and press There are no negative terms in the Y 1 table. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 c Solve the equation by graphing the related function. –x 2 + 4 = 0 Step 1 Write the related function. y = –x 2 + 4 Step 2 Graph the function. Use a graphing calculator. Step 3 Find the zeros. The function appears to have zeros at (2, 0) and (– 2, 0). Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 1 c Continued Solve the equation by graphing the related function. –x 2 + 4 = 0 The equation has two real-number solutions. Check reasonableness Use the table function. There are two zeros in the Y 1 column. The function appears to have zeros at – 2 and 2. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2: Application A frog jumps straight up from the ground. The quadratic function f(t) = – 16 t 2 + 12 t models the frog’s height above the ground after t seconds. About how long is the frog in the air? When the frog leaves the ground, its height is 0, and when the frog lands, its height is 0. So solve 0 = – 16 t 2 + 12 t to find the times when the frog leaves the ground and lands. Step 1 Write the related function 0 = – 16 t 2 + 12 t y = – 16 t 2 + 12 t Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2 Continued Step 2 Graph the function. Use a graphing calculator. Step 3 Use to estimate the zeros. The zeros appear to be 0 and 0. 75. The frog leaves the ground at 0 seconds and lands at 0. 75 seconds. The frog is off the ground for about 0. 75 seconds. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Example 2 Continued Check 0 = 0 0 Holt Algebra 1 – 16 t 2 + 12 t – 16(0. 75)2 + 12(0. 75) – 16(0. 5625) + 9 – 9 + 9 0 Substitute 0. 75 for x in the quadratic equation.

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 2 What if…? A dolphin jumps out of the water. The quadratic function y = – 16 x 2 + 32 x models the dolphin’s height above the water after x seconds. About how long is the dolphin out of the water? When the dolphin leaves the water, its height is 0, and when the dolphin reenters the water, its height is 0. So solve 0 = – 16 x 2 + 32 x to find the times when the dolphin leaves and reenters the water. Step 1 Write the related function 0 = – 16 x 2 + 32 x y = – 16 x 2 + 32 x Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 2 Continued Step 2 Graph the function. Use a graphing calculator. Step 3 Use to estimate the zeros. The zeros appear to be 0 and 2. The dolphin leaves the water at 0 seconds and reenters at 2 seconds. The dolphin is out of the water for about 2 seconds. Holt Algebra 1

Solving Quadratic Equations 9 -5 by Graphing Check It Out! Example 2 Continued Check 0 = – 16 x 2 + 32 x 0 – 16(2)2 + 32(2) 0 – 16(4) + 64 0 – 64 + 64 0 Holt Algebra 1 0 Substitute 2 for x in the quadratic equation.

Solving Quadratic Equations 9 -5 by Graphing Lesson Quiz Solve each equation by graphing the related function. 1. 3 x 2 – 12 = 0 2, – 2 2. x 2 + 2 x = 8 – 4, 2 3. 3 x – 5 = x 2 no solution 4. 3 x 2 + 3 = 6 x 1 5. A rocket is shot straight up from the ground. The quadratic function f(t) = – 16 t 2 + 96 t models the rocket’s height above the ground after t seconds. How long does it take for the rocket to return to the ground. 6 s Holt Algebra 1