5 1 GRAPHING QUADRATIC FUNCTIONS I can graph

5. 1 GRAPHING QUADRATIC FUNCTIONS I can graph quadratic functions in standard form. I can graph quadratic functions in vertex form. I can graph quadratic functions in intercept form. You NEED graph paper today!

QUADRATIC FUNCTION? We’ve been working with functions in the form y = mx + b. This was called a linear function because the graph was a straight line. A quadratic function is the form: y = ax 2 + bx + c where a ≠ 0 The graph of a quadratic function is: A parabola What’s d ifferent between a linear function and a quadrati c functio n?

QUADRATIC FUNCTION IN STANDARD FORM Y = AX 2 + BX + C Vertex Can either be the minimum of the parabola or the maximum of the parabola. If a is positive… The parabola goes up (like a cup) If a is negative… The parabola goes down (like a frown)

QUADRATIC FUNCTION Y = AX 2 + BX + C Axis of symmetry Parabolas are always symmetric. Makes a vertical ‘imaginary’ line at the x coordinate of the vertex that cuts the parabola into equal halves.

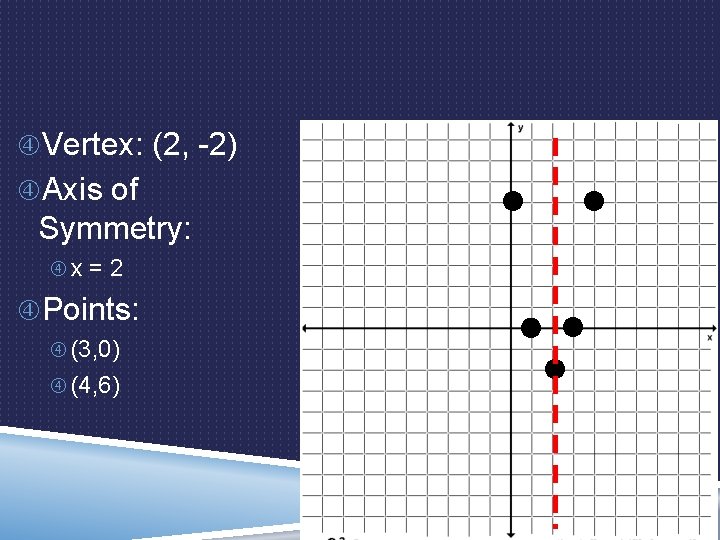
EXAMPLE 1: Standard Form: GRAPHING A QUADRATIC FUNCTION y = ax 2 + bx + c IN STANDARD FORM a= 2 b= -8 c= 6 y = 2(2)2 – 8(2) + 6 y = 2(4) – 16 + 6 y = 8 -10 y = -2 ) 2 , (2

Axis of Symmetry: x = 2 y = 2(3)2 – 8(3) + 6 y = 2(9) – 24 + 6 y = 18 – 24 + 6 You also need two more points to be able to make the graph. y = 0 (3, 0) 2 – 8(4) + 6 y = 2(4) Choose x = 3 and x = 4 because they are right after the Axis of Symmetry y = 2(16) – 32 + 6 y = 32 – 32 + 6 y = 6 (4, 6)

Vertex: (2, -2) Axis of Symmetry: x = 2 Points: (3, 0) (4, 6)

INDIVIDUAL PRACTICE ON GRAPHING QUADRATICS IN STANDARD FORM Pg 253 20 -25 You have 15 minutes to work on this section of problems. List the vertex Axis of symmetry At least 2 extra points I will do the next part of notes in 15 minutes.

QUADRATIC FUNCTION IN VERTEX FORM y = a(x – h)2 + k Vertex: (h, k) Axis of Symmetry: x = h You still also need to find two more points to plot.

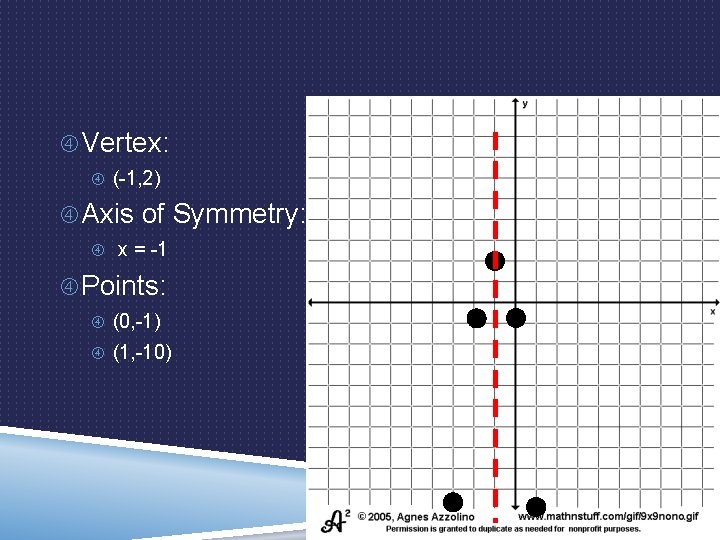
Vertex Form: EXAMPLE 2: GRAPHING A QUADRATIC 2 + k y = a(x – h) FUNCTION IN VERTEX FORM y = -3(x + 1)2 + 2 Vertex: (-1, 2) Axis of Symmetry: x = -1 Points: x = 0 y = -3(0+1)2 + 2 y = -3(1) + 2 y = -3 + 2 y = -1 x = 1 y = -3(1+1)2 + 2 (0, -1) y = -3(2)2 + 2 (1, -10) y = -3(4) + 2 y = -12 + 2 y = -10

Vertex: (-1, 2) Axis of Symmetry: x = -1 Points: (0, -1) (1, -10)

INDIVIDUAL PRACTICE ON GRAPHING QUADRATICS IN VERTEX FORM Pg. 253 26 -31 You have 15 minutes to work on this section of problems. List the vertex Axis of symmetry At least 2 extra points I will do the next part of notes in 15 minutes.

QUADRATIC FUNCTIONS IN INTERCEPT FORM y = a(x – p)(x – q) The x-intercepts are p and q. The axis of symmetry is halfway between p and q. The vertex is found by plugging the axis of symmetry back in to the function and solve for y.

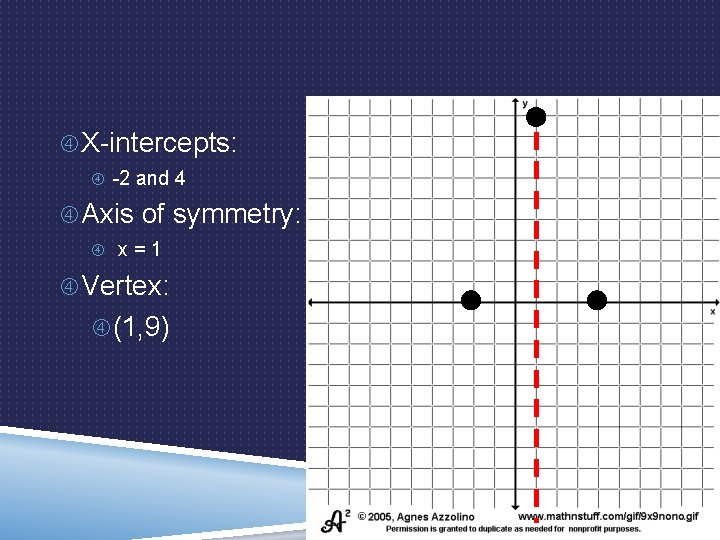
Intercept Form: EXAMPLE 3: GRAPHING QUADRATICS y = a(x – p)(x – q) IN INTERCEPT FORM y = -(x + 2)(x - 4) X-intercepts: -2 and 4 Axis of symmetry: x = 1 Vertex: (1, 9) x = 1 y = -(1+2)(1 -4) y = -(3)(-3) y = -(-9) y = 9

X-intercepts: -2 and 4 Axis of symmetry: x = 1 Vertex: (1, 9)

INDIVIDUAL PRACTICE ON GRAPHING QUADRATICS IN INTERCEPT FORM Pg. 254 32 -37 List the vertex Axis of symmetry Intercepts