1 Quadratic functions A Quadratic functions B Quadratic

1 Quadratic functions A. Quadratic functions B. Quadratic equations C. Quadratic inequalities

2 A. Quadratic functions

3 A. Quadratic functions Example Remember exercise 4 (linear functions): For a local pizza parlor the weekly demand function is given by p=26 -q/40. Express the revenue as a function of the demand q. Solution: revenue= price x quantity = 26 q –q²/40

4 A. Quadratic functions Example Group excursion ♦ ♦ Minimum 20 participants Fixed cost: 122 EUR For 20 participants: 80 EUR person For every supplementary participant: for everybody (also the first 20) a price reduction of 2 EUR per supplementary participant Revenue of the travel agency when there are 6 supplementary participants? total revenue = 122 + (20 + 6) (80 6 2) = 1890

5 A. Quadratic functions Example Group excursion ♦ ♦ Minimum 20 participants Fixed cost: 122 EUR For 20 participants: 80 EUR person For every supplementary participant: for everybody (also the first 20) a price reduction of 2 EUR per supplementary participant Revenue y of the travel agency when there are x supplementary participants? total revenue = y = 122 + (20 + x) (80 x 2) = 2 x 2 + 40 x + 1722

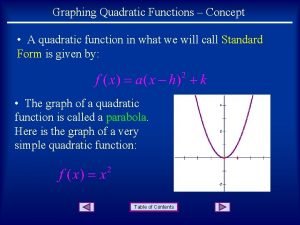
6 A. Quadratic functions revenue function y = 2 x 2 + 40 x + 1722 is a quadratic function Definition A function f is a quadratic function if and only if its equation can be written in the form f(x) = y = ax² + bx + c where a, b and c are constants and a 0. (Section 3. 3 p. 141)

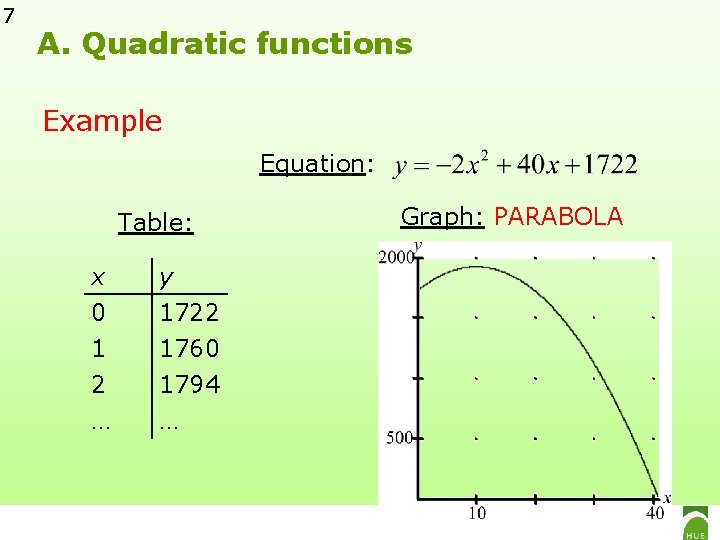
7 A. Quadratic functions Example Equation: Table: x 0 1 2 y 1722 1760 1794 … … Graph: PARABOLA

8 B. Quadratic equations

9 B. Quadratic equations Example Group excursion Revenue equal to 1872? 2 x² + 40 x + 1722 = 1872 2 x² + 40 x + 1722 1872 = 0 2 x² + 40 x 150 = 0 We have to solve the equation 2 x² + 40 x 150 = 0 Quadratic equation

10 B. Quadratic equations Definition A quadratic equation is an equation that can be written in the form ax² + bx + c = 0 where a, b and c are constants and a 0. (Section 0. 8 p. 36)

11 B. Quadratic equations Solving a quadratic equation - strategy 1: based on factoring, … Exercises 1. Solve x²+x 12=0 (Section 0. 8 – example 1 p. 36) 2. Solve (3 x 4)(x+1)= 2 (Section 0. 8 – example 2 p. 37) 3. Solve 4 x 4 x³=0 (Section 0. 8 – example 3 p. 37) 4. Solve 5. Solve x²=3 (Section 0. 8 – ex. 4 p. 37) (Section 0. 8 – example 5 p. 38)

12 B. Quadratic equations Solving a quadratic equation - strategy 2: formula based on the discriminant Discriminant = d = b² 4 ac • if d > 0: two solutions: • if d = 0: one solution: • if d < 0: no solutions ,

13 B. Quadratic equations Exercises 1. Solve 4 x² - 17 x + 15 = 0 (Section 0. 8 – example 6 p. 36) 2. Solve 2 x² + 40 x 150 = 0 3. Solve 2 + 6 y + 9 y² = 0 (example slide 9) (Section 0. 8 – example 7 p. 37) 4. Solve z² + z + 1 = 0 (Section 0. 8 – example 8 p. 37) 5. Solve (Section 0. 8 – example 9 p. 37) Supplementary exercises: exercise 1

14 A. Quadratic functions

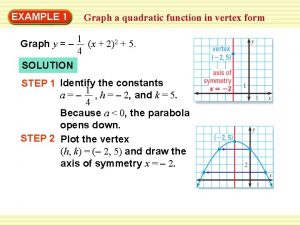
15 A. Quadratic functions Graph Quadratic functions: graph is a PARABOLA What does the sign of a mean? ♦ if a>0, the parabola opens upward ♦ if a<0, the parabola opens downward Example (group excursion) y = 2 x² + 40 x + 1722 a = 2 < 0 (Section 3. 3 p. 142 -144)

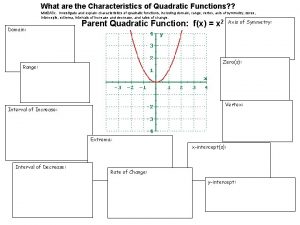
16 A. Quadratic functions Graph Quadratic functions: graph is a PARABOLA Graphical interpretation of y=ax²+bx+c=0? Sign of the discriminant determines the number of intersections with the horizontal axis Zero’s, also called x-intercepts, solutions of the quadratic equation y=ax²+bx+c=0, correspond to intersections with the horizontal x-axis Example Group excursion: y=-2 x²+40 x+1722 d=124²>0 x=41; (x=-21)

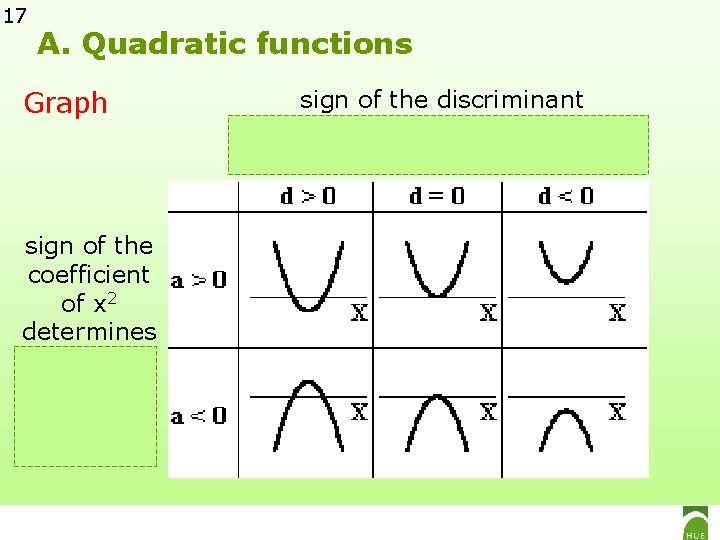
17 A. Quadratic functions Graph sign of the coefficient of x 2 determines the orientation of the opening sign of the discriminant determines the number of intersections with horizontal axis

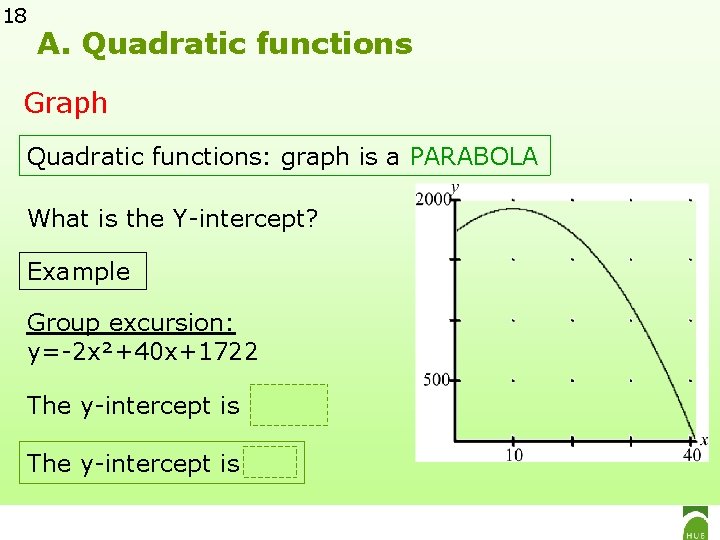
18 A. Quadratic functions Graph Quadratic functions: graph is a PARABOLA What is the Y-intercept? Example Group excursion: y=-2 x²+40 x+1722 The y-intercept is 1722. The y-intercept is c.

19 A. Quadratic functions Graph Each parabola is symmetric about a vertical line. Which line ? Both parabola’s at the right show a point labeled vertex, where the symmetry axis cuts the parabola. If a>0, the vertex is the “lowest” point on the parabola. If a<0, the vertex refers to the “highest” point. x-coordinate of vertex equals -b/(2 a) axis of symmetry is line x=-b/(2 a) x = -b/(2 a) • •

20 A. Quadratic functions Example Group excursion: Maximum revenue? vertex is “highest” point x-coordinate of vertex equals -b/(2 a) maximum revenue = y-coo of vertex = y(10) = 1922

21 A. Quadratic functions Example Group excursion: Maximum revenue? In this case you can find it e. g. using the table: So: 10 supplementary participants (30 participants in total)

22 A. Quadratic functions Exercises 1. Graph the quadratic function y = -x² - 4 x + 12. Sign a? Sign d? Zeros? Y-intercept? Vertex? (Section 3. 3 – example 1 p. 143) 2. A man standing on a pitcher’s mound throws a ball straight up with an initial velocity of 32 feet per second. The height of the ball in feet t seconds after it was thrown is described by the function h(t)= 16 t²+32 t+8 for t ≥ 0. What is the initial height of the ball? What is the maximum height? When is the ball back at a height of 8 feet? (Section 3. 2 – Apply it 14 p. 144)

23 A. Quadratic functions Supplementary exercises • • Exercise 2 (f 1 and f 5), Exercise 3, 7, 5 rest of exercise 2 Exercise 4, 6, 8 and 9

24 A. Quadratic functions Supplementary exercises Exercise 7 line parabola

25 C. Quadratic inequalities

26 C. Quadratic inequalities Definition A quadratic inequality is one that can be written in the form ax² + bx + c ‘unequal’ 0, where a, b and c are constants and a 0 and where ‘unequal’ stands for <, , > or . Example Solve the inequality i. e. find all x for which standard form

27 C. Quadratic inequalities Example 1. Write in standard form: 2. Study the equality: x = -2; x = 7 3. Determine type of graph: 4. Solve inequality: conclusion: x -2 or x 7 interval notation: ]- , -2] [7, [

28 C. Quadratic inequalities that can be reduced to the form determine the common points with the x-axis by solving the EQUATION and …

29 C. Quadratic inequalities Supplementary exercises • • Exercise 10 (a) Exercises 11 (a), (c) Exercises 10 (b), (c), (d) Exercises 11 (b), (d)

30 Quadratic functions Summary • Quadratic equations: discriminant d, solutions • Quadratic functions: ♦ ♦ ♦ ♦ graph: parabola sign of d zeroes vertex symmetry axis minimum/maximum • Quadratic inequalities: solutions

31 Quadratic functions Extra exercises: Handbook – Problems 0. 8: Ex 31, 37, 45, 57, 79 Problems 3. 3: Ex 11, 13, 29, 37, 41