Quadratic Theory Higher Maths Quadratic Theory The quadratic

Quadratic Theory Higher Maths

Quadratic Theory The quadratic graph Using the discriminant Ans Quadratic theory examples Basic skills questions Ans Problem solving questions Past paper questions Click on a topic Ans

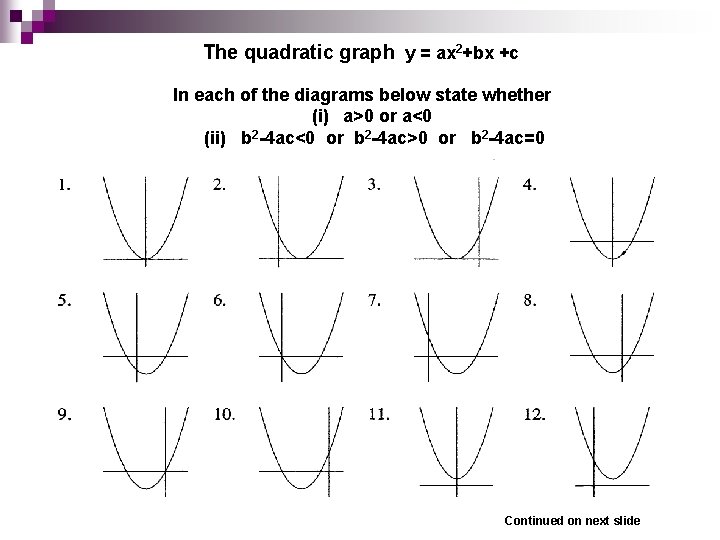
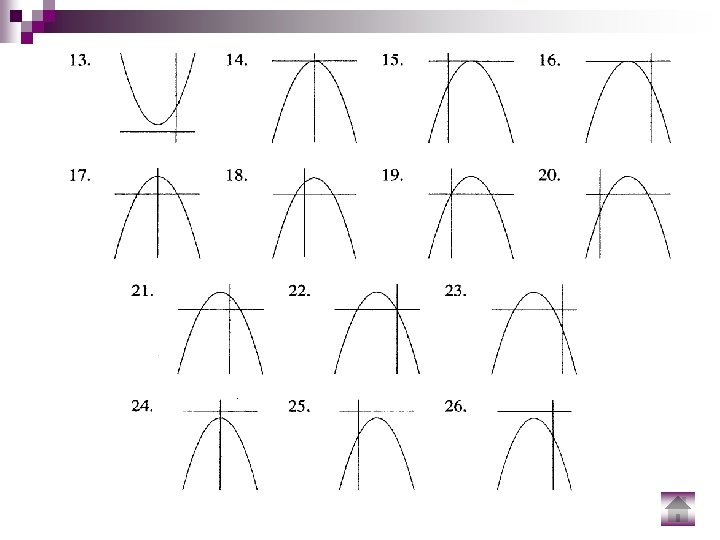
The quadratic graph y = ax 2+bx +c In each of the diagrams below state whether (i) a>0 or a<0 (ii) b 2 -4 ac<0 or b 2 -4 ac>0 or b 2 -4 ac=0 Continued on next slide

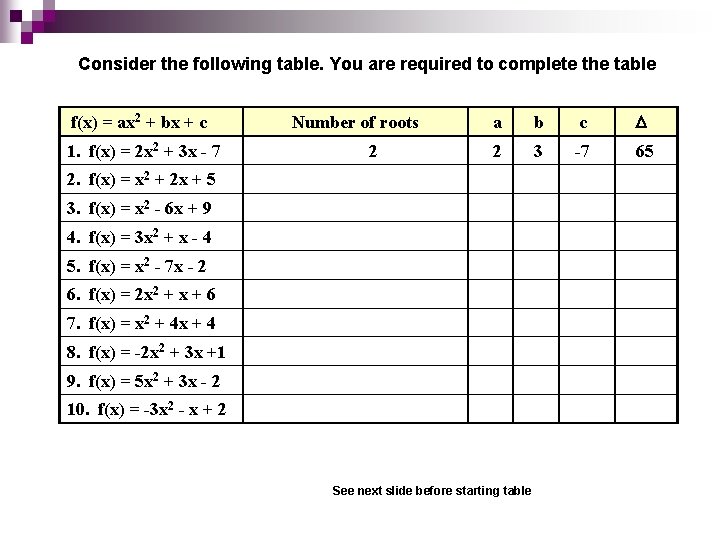
Using the Discriminant In the solution of the quadratic equation ax 2 + bx + c = 0 the solutions are given by The quantity b 2 - 4 ac is important. It is called the discriminant. It can be used to tell what kind of roots the equation will have. The table on the next slide investigates this idea. Continued on next slide

Consider the following table. You are required to complete the table f(x) = ax 2 + bx + c 1. f(x) = 2 x 2 + 3 x - 7 Number of roots 2 a b c D 2 3 -7 65 2. f(x) = x 2 + 2 x + 5 3. f(x) = x 2 - 6 x + 9 4. f(x) = 3 x 2 + x - 4 5. f(x) = x 2 - 7 x - 2 6. f(x) = 2 x 2 + x + 6 7. f(x) = x 2 + 4 x + 4 8. f(x) = -2 x 2 + 3 x +1 9. f(x) = 5 x 2 + 3 x - 2 10. f(x) = -3 x 2 - x + 2 See next slide before starting table

You could use the graphic calculator for this work if you wish. Enter the function in Y 1. Press ZOOM and select 6: ZStandard Draw each graph and determine the number of roots the quadratic has. Enter the values of a , b and c and evaluate D. Examine the table carefully and make some conjectures about the connection between the value of b 2 - 4 ac and the number of roots of the corresponding quadratic equation.

Quadratic Theory Examples [ y = ax 2+bx +c ] 1. Choose one of either 2. a > 0 or a < 0 and one of b 2 – 4 ac > 0 b 2 – 4 ac = 0 b 2 – 4 ac < 0 corresponding to each of the six graphs below. Continued on next slide

2. Use the discriminant b 2 – 4 ac to find the nature of the roots of the equations below. a) 2 x 2 – 7 x + 1 = 0 b) 5 x 2 + 2 x + 2 = 0 c) 9 x 2 – 24 x + 16 = 0 d) x 2 + x + 7 = 0 e) 6 x 2 – x – 1 = 0 f) 3 x 2 + 2 x + 5 = 0 3. Examine the discriminant to see if the roots of the following equations are real, equal or imaginary. a) 2 x 2 – 5 x – 1 = 0 b) x 2 + x + 7 = 0 c) 3 x 2 – 18 x + 27 = 0 d) 2 x 2 + x + 1 = 0 4. Find k given that each of the following equations has equal roots. a) x 2 – 8 x + k = 0 b) kx 2 – 12 x + 9 = 0 c) x 2 + kx + 16 = 0 5. Find m if x 2 + 2 mx + 9 = 0 has equal roots. Continued on next slide

6. Find p if x 2 + (p + 1)x + 9 = 0 has real distinct roots. 7. Find p if (p + 1)x 2 – 2(p + 3)x + 3 p = 0 has equal roots. 8. find c if x 2 + (x + c)2 = 8 has equal roots. 9. Show that the roots of k(x + 1)(x + 4) = x are not real if <k<1 10. Find m if x 2 + (mx – 5)2 = 9 has equal roots. 11. If = n form a quadratic equation in x and show that, for real x, n – 3 or n 2. Solutions on next slide

Quadratics Solutions 1. i) a < 0 iii) a > 0 v) a > 0 2. a) b) c) d) e) f) b 2 – 4 ac > 0 ii) b 2 – 4 ac = 0 b 2 – 4 ac 0 a > 0 b 2 – 4 ac < 0 iv) a < 0 b 2 – 4 ac = 0 vi) a < 0 b 2 – 4 ac < 0 D = 41 roots are real and distinct D = – 36, no roots D = 0, roots are equal D = – 27, no roots D = 25 , roots are real and distinct D = – 56, no roots Continued on next slide

3. a) b) c) d) (– 5)2 – 4. 2. (– 1) = 33 12 – 4. 1. 7 = – 27 (– 18)2 – 4. 3. 27 = 0 12 – 3. 2. 1 = – 7 4. a) b) c) (– 8)2 – 4. 1. k = 0 , 64 – 4 k = 0 , k = 16 (– 12)2 – 4. k. 9 = 0 , 144 – 36 k = 0 , k = 4 k 2 – 4. 1. 16 = 0 , k 2 = 64 , k = 8 5. (2 m)2 – 4. 1. 9 = 0 , 4 m 2 = 36 , m 2 = 9 , m = 3 6. (p + 1)2 – 4. 1. 9 > 0 , (p + 1)2 – 62 > 0 , (p – 5)(p + 7) > 0 p < – 7 or p > 5 7. real roots imaginary roots equal roots imaginary roots [– 2(p + 3)]2 – 4(p + 1)(3 p) = 0 4(p 2 + 6 p + 9) – 12 p 2 – 12 p = 0 4 p 2 + 24 p + 36 – 12 p 2 – 12 p = 0 2 p 2 – 3 p – 9 = 0 (p – 3)(2 p + 3) = 0 p = – 3/2 or p = 3 Continued on next slide

8. x 2 + (x + c)2 = 8 2 x 2 + 2 cx + c 2 – 8 = 0 This has equal roots when (2 c)2 – 4(2)(c 2 – 8) = 0 4 c 2 – 8 c 2 + 64 = 0 4 c 2 = 64 c= 4 9. k(x + 1)(x + 4) = x kx 2 + (5 k – 1)x + 4 k = 0 This has imaginary roots if (5 k – 1)2 – 4(k)(4 k) < 0 25 k 2 – 10 k + 1 < 0 9 k 2 – 10 k + 1 < 0 (k – 1)(9 k – 1) < 0 <k<1 Continued on next slide

10. x 2 + (mx – 5)2 = 9 (m 2 + 1) – 10 mx + 16 = 0 This has equal roots when (– 10 m)2 – 4(m 2 + 1)(16) = 0 100 m 2 – 64 = 0 36 m 2 – 64 = 0 9 m 2 = 16 m = 4/3 11. x 2 + 4 x + 10 = n(2 x + 5) x 2 + (4 – 2 n)x + 10 – 5 n = 0 This has real roots when (4 – 2 n)2 – 4(1)(10 – 5 n) 0 16 – 16 n + 4 n 2 – 40 + 20 n o 4 n 2 + 4 n – 24 o n 2 + n – 6 0 (n + 3)(n – 2) 0 n – 3 or n 2

Quadratic theory - Basic skills questions

Basic skills - Solutions

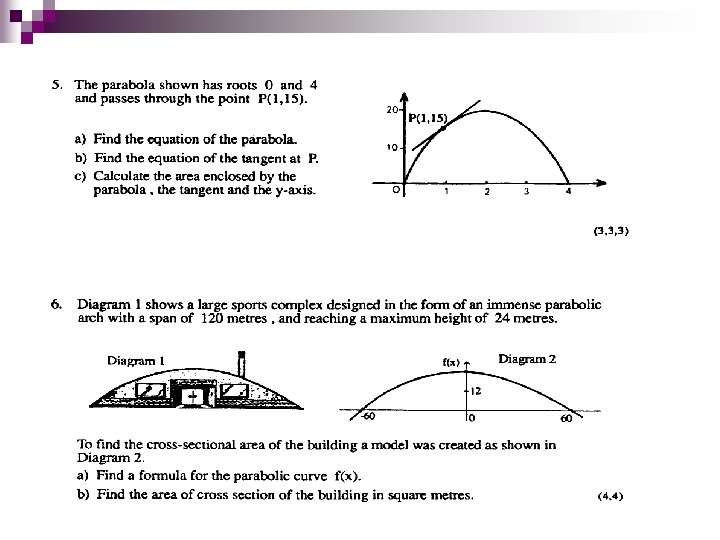
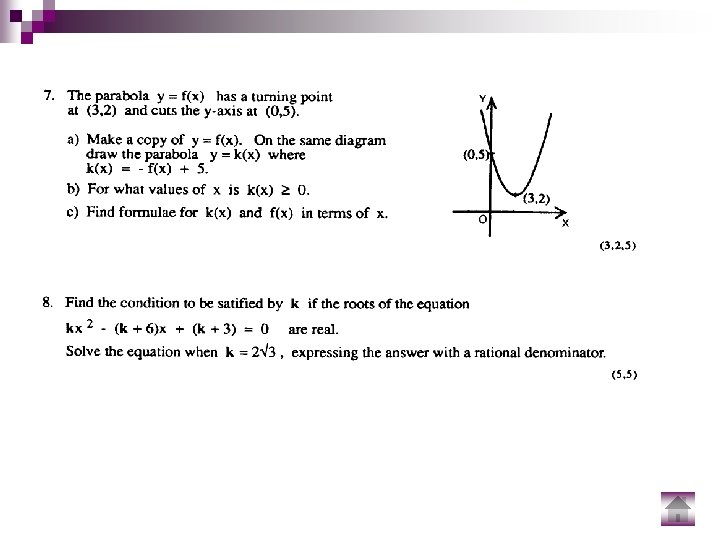
Quadratic Theory – Problem solving questions

Quadratic Theory Exam Level Questions/ Past Paper questions. 1. For what values of ‘p’ does the equation x 2 – 2 x + p = 0 have equal roots. 2. Show that the roots of the quadratic (k-2)x 2 – (3 k-2)x + 2 k = 0 are always real. 3. If ‘k’ is a real number show that the roots of the equation kx 2 + 3 x + 3 = k are always real. 4. The roots of the equation (x+1)(x+k) = -4 are equal. Find the value of ‘k’. 5. Find the values of ‘k’ for which the equation 2 x 2 + 4 x – k = 0 has equal roots. 6. Calculate the least positive integer ‘k’ so that the graph shown does not cut or touch the x axis. (0, k) y = kx 2 -8 x + k

7. Show that the equation (1 -2 k)x 2 – 5 kx - 2 k = 0 has real roots for all integer values of ‘k’. 8. For what values of ‘k’ has the equation x 2 – 5 x + (k+6) = 0 have equal roots? 9. If f(x) = 2 x+1 and g(x) = x 2 + k, show that the equation g(f(x)) – f(g(x)) = 0 reduces to 2 x 2 + 4 x – k = 0 and find the value of ‘k’ for which this equation has equal roots. What kind of roots does this equation have when k=6? 10. For what values of ‘k’ does the equation 5 x 2 – 2 x + k = 0 have real roots? 11. For what value of ‘a’ does the equation ax 2 + 20 x + 40 = 0 have equal roots? 12. Find ‘p’ given that the equation x 2 + (px – 5)2 = 9, has equal roots.

13. Given that , form a quadratic equation in x and hence show that if of the equation are real. or then the roots 14. Find ‘m’ if the equation (2 m-1)x 2 + (m+1)x + 1 = 0 has equal roots. If m lies between these values find the nature of the roots. 15. Show that the roots of the equation k(x+1)(x+4) = x are not real if <k<1. 16. Find ‘k’ given that the equation kx 2 + (2 k+1)x + k = 0 has equal roots. 17. If ‘k’ is a real number, show that the roots of the equation , are always real.

18. For what values of ‘k’ does the equation x(x-4) + 2 = k(2 x – 3 k) have real roots? 19. Show that the line y = x + c meets the parabola y = x 2 – 3 x where x 2 – 4 x – c = 0. Find the value of ‘c’ if the line is a tangent to the parabola. 20. Find the value of ‘n’ if the equation , is to have equal roots.

Answers – Exam level questions Q 1. p = 1 Q 2. (k+2)2 is always greater than or equal to 0 because it is a quantity squared. Q 3. (2 k-3)2 is always greater than or equal to 0 because it is a quantity squared. Q 4. k = 5, k = -3 Q 5. k = -2 Q 6. No roots if k<-4 or k>4 therefore the smallest positive integer k is k = 5 Q 7. b 2 – 4 ac = 0 when k=0 or k = -8/9 therefore real for all integer values of k. Q 8. k = 0. 25 Q 9. k = -2 ; If k = 6 there are two real distinct roots. Q 10. k Q 11. a = 2. 5 Q 12. p = 4/3 , p = -4/3 Q 13. n 2 or n -3 Q 14. m = 1, 5 Q 15. No roots for <k<1

Q 16. Q 17. Q 18. Q 19. Q 20. k = -1/4 Roots are not always real. The roots are real if k Real roots if k is between (1 - 2) and (1+ 2) c = -4 n = 0 and n = 3 2 or k