Identifying Quadratic Functions Lesson 8 1 What does














































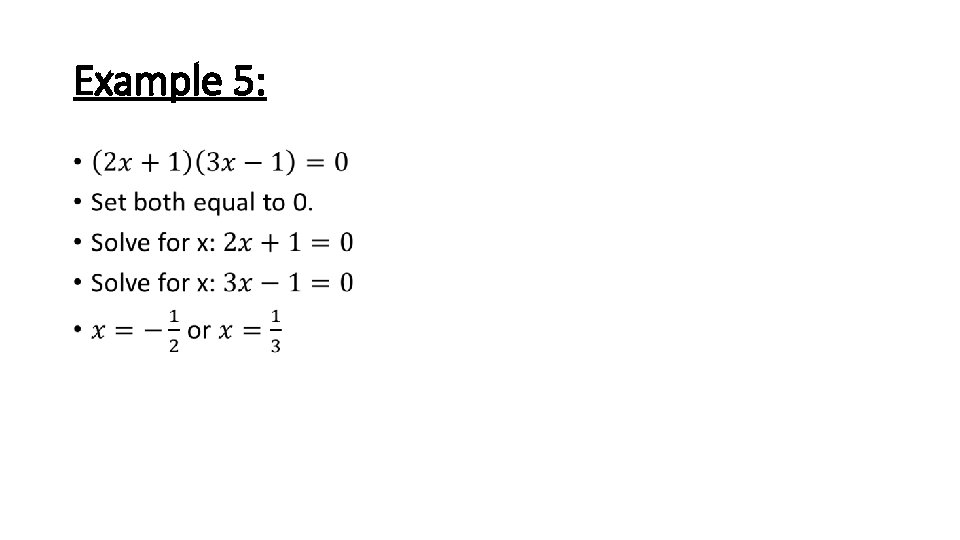










- Slides: 68

Identifying Quadratic Functions Lesson 8 -1

What does a quadratic equation (or function) look like? •

Example 1: Tell whether the equation (or function) is quadratic. •

Example 2: Tell whether the equation (or function) is quadratic continued. •

Example 3: Tell whether the equation (or function) is quadratic continued. •

Your Turn: Tell whether the function is quadratic. •

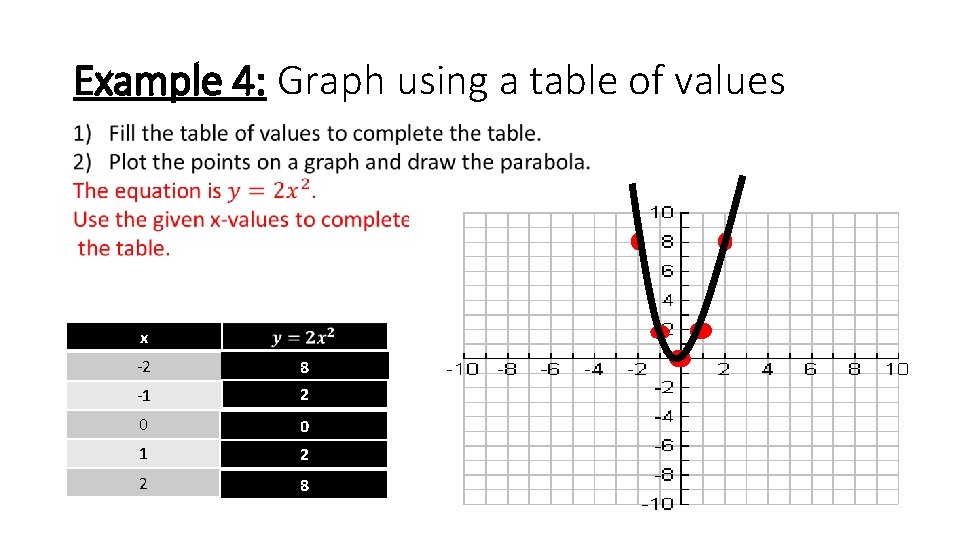
Example 4: Graph using a table of values x -2 8 -1 2 0 0 1 2 2 8

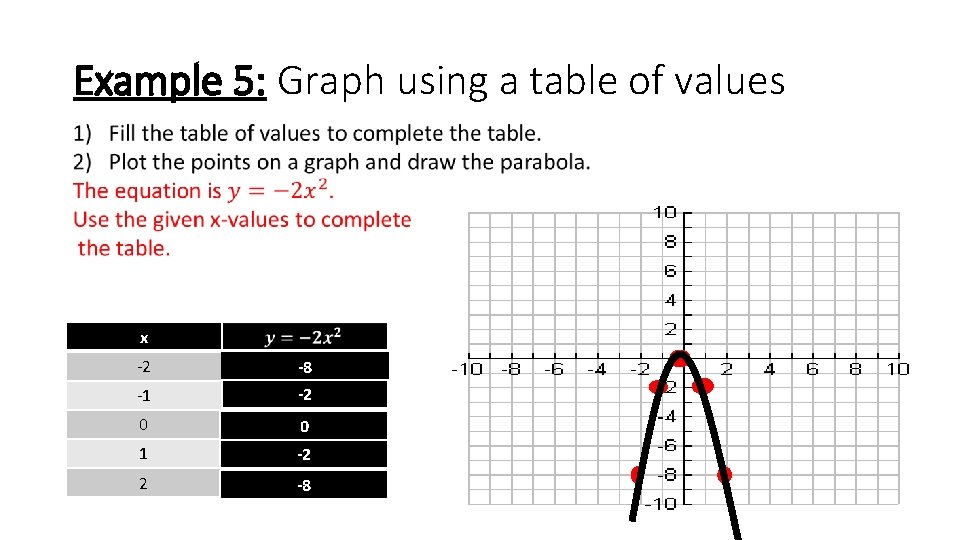
Example 5: Graph using a table of values x -2 -8 -1 -2 0 0 1 -2 2 -8

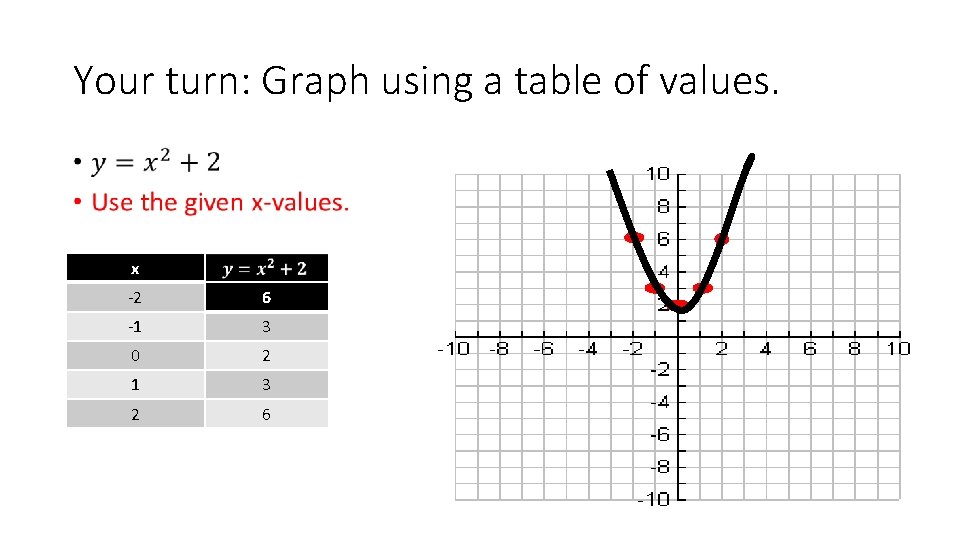
Your turn: Graph using a table of values. • x -2 6 -1 3 0 2 1 3 2 6

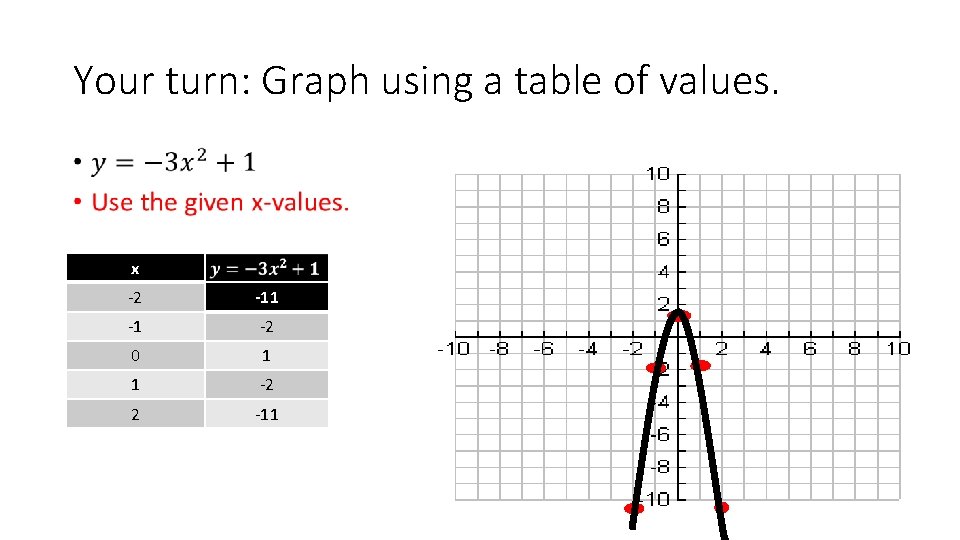
Your turn: Graph using a table of values. • x -2 -11 -1 -2 0 1 1 -2 2 -11



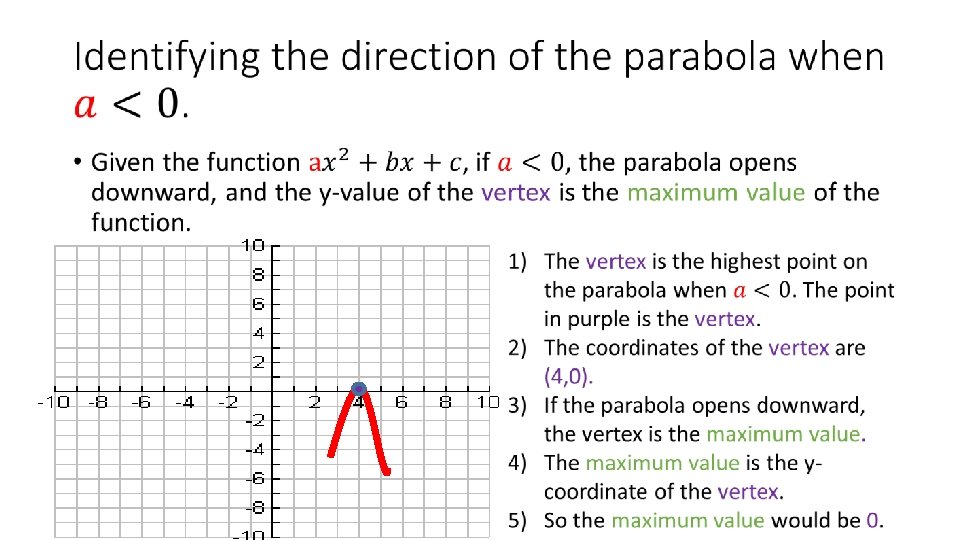
Example 6: Tell whether the graph of each quadratic function opens upward or downward. •

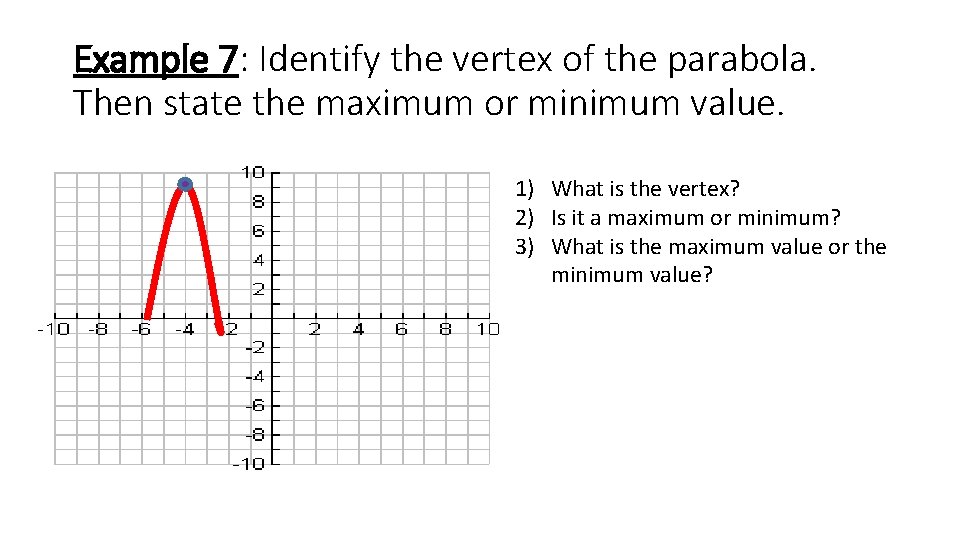
Example 7: Identify the vertex of the parabola. Then state the maximum or minimum value. 1) What is the vertex? 2) Is it a maximum or minimum? 3) What is the maximum value or the minimum value?

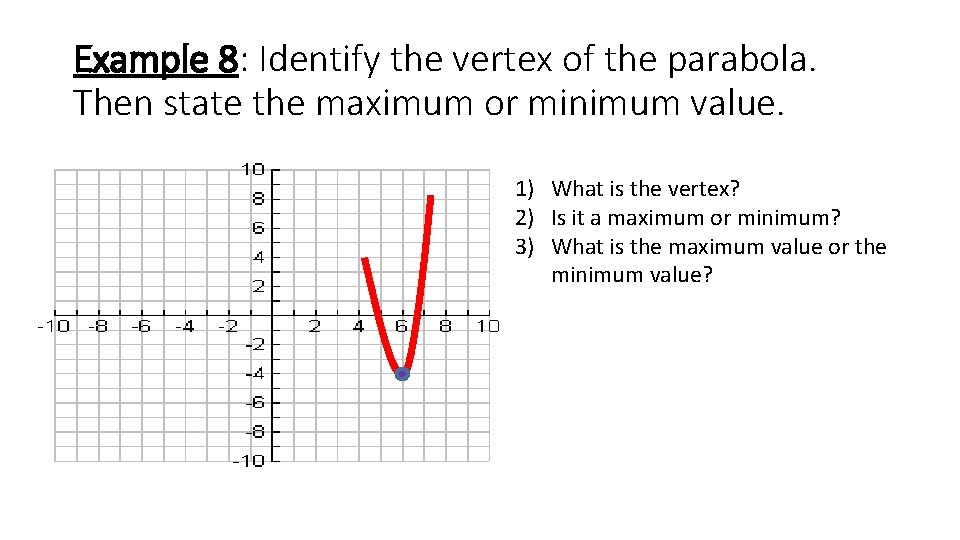
Example 8: Identify the vertex of the parabola. Then state the maximum or minimum value. 1) What is the vertex? 2) Is it a maximum or minimum? 3) What is the maximum value or the minimum value?

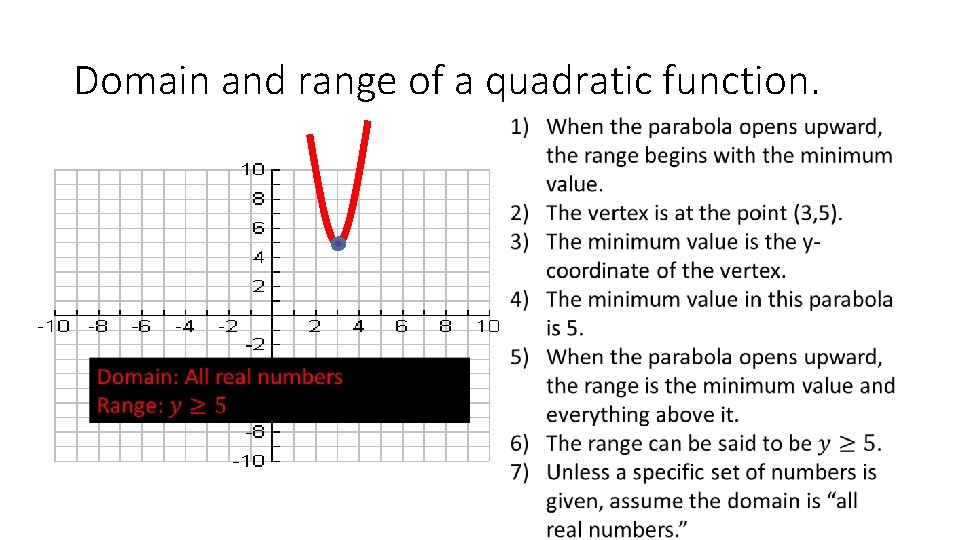
Domain and range of a quadratic function.

Domain and range of a quadratic function.

Recap… •

Recap… •

Homework • Page 527 (26, 28, 30 – 38 all)

Characteristics of Quadratic Functions Lesson 8 -2

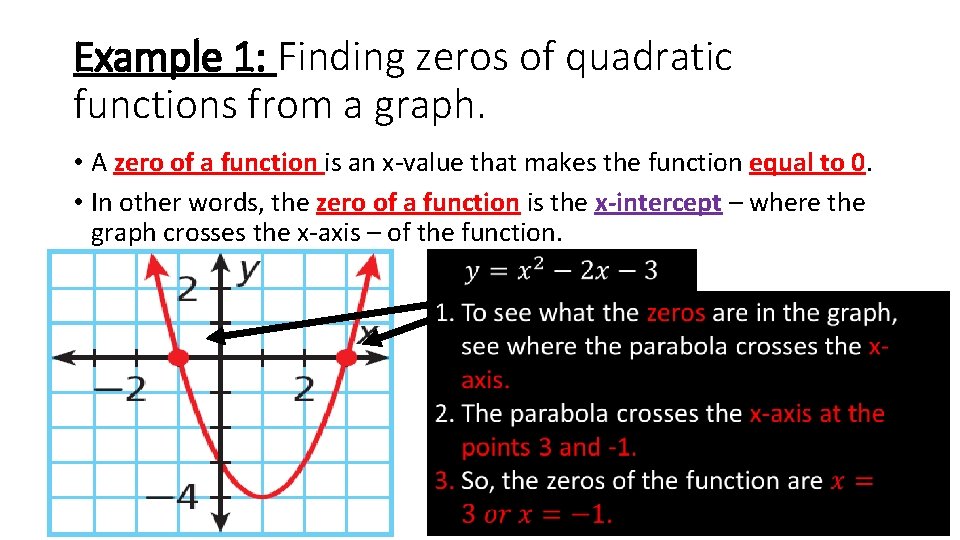
Example 1: Finding zeros of quadratic functions from a graph. • A zero of a function is an x-value that makes the function equal to 0. • In other words, the zero of a function is the x-intercept – where the graph crosses the x-axis – of the function.

Example 2: Finding zeros of quadratic functions from a graph. • A zero of a function is an x-value that makes the function equal to 0. • In other words, the zero of a function is the x-intercept – where the graph crosses the x-axis – of the function.

Example 3: Finding zeros of quadratic functions from a graph.

Example 4: Finding zeros of quadratic functions from a graph. 1. To see what the zeros are in the graph, see where the parabola crosses the xaxis. . 2. The parabola does NOT cross the x-axis!!! 3. So, there are no zeros of the function.

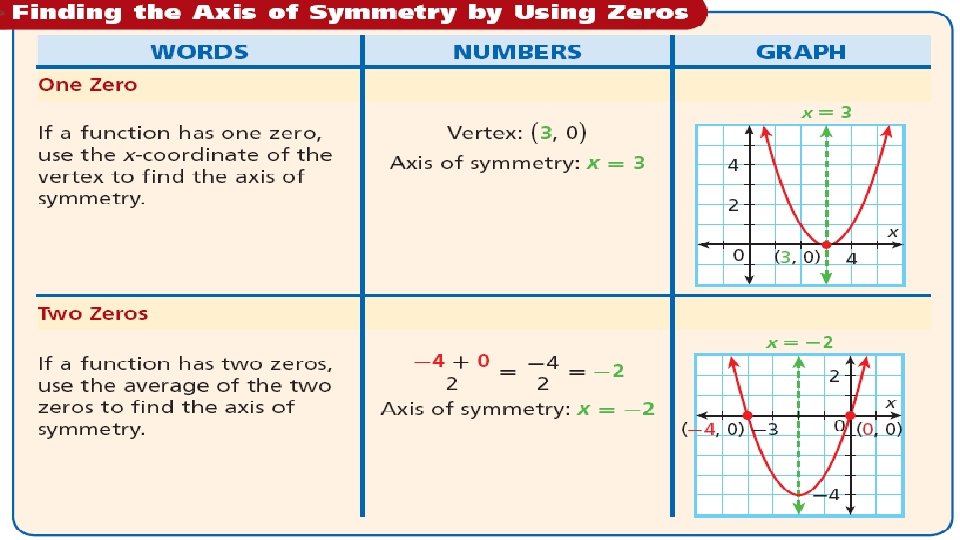
Finding the axis of symmetry. • The axis of symmetry is a vertical line that divides the parabola into two symmetrical sides. • The axis of symmetry passes through the vertex. We are going to use the zeros to find the axis of symmetry.


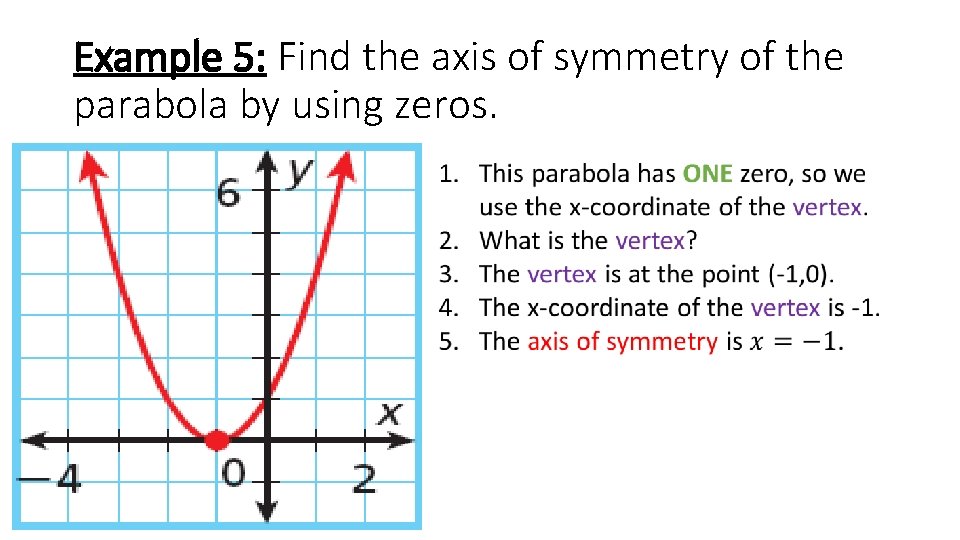
Example 5: Find the axis of symmetry of the parabola by using zeros.

Example 6: Find the axis of symmetry of the parabola by using zeros.

Formula for computing the axis of symmetry. • You can use this formula if there are no zeros or the zeros are hard to identify from a graph. This formula works for all quadratic functions.

Example 7: Find the axis of symmetry by using the formula. •

Example 8: Find the axis of symmetry by using the formula. •

Practice (Still part of notes). • Page 535 (3 -6, 8, 9, 12)

Finding the vertex of a parabola • Since we know how to find the axis of symmetry, we can now find the vertex of a parabola using the following steps. 1. Find the axis of symmetry of the parabola (x =). 2. Plug in the x-value into the equation to find the y-value. 3. Write the vertex as an ordered pair.

Example 9: Find the vertex of the parabola. •

Example 9 Continued: Find the vertex of the parabola. •

Example 9 Continued: Find the vertex of the parabola. •

Example 10: Find the vertex of the parabola. •

Example 10 Continued: Find the vertex of the parabola. •

Homework • Page 536 (19 -23, 25, 26, 29 -31)

Transforming Quadratic Functions Lesson 8 -4

The basics… •


• The bigger the number, the skinnier the parabola. • The smaller the number, the fatter the parabola.

Example 1: Order the functions from skinniest to fattest. •

Vertical Translations


Recap… •

Homework • Page 549 (10 -17) • Page 553 (1 -16, 21 -24) (I know it says quiz at the top, but this is your study guide for the test!)

Solving Quadratic Equations by Factoring Lesson 8 -6

Remember Factoring? •

Example 1: Solving quadratics by factoring. •

Example 1: Solving quadratics by factoring continued. •

Example 2: •

Example 3: •

Example 4: •

Example 4 Continued: •
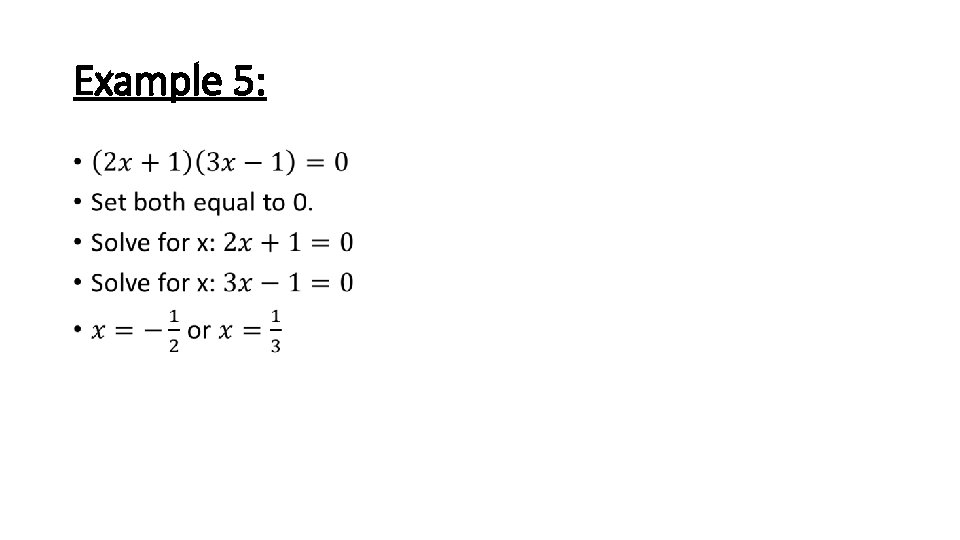
Example 5: •

Example 6: • 2

Homework • Page 565 (2 -18)

Solving Quadratic Equations by Using Square Roots Lesson 8 -7

Square Roots • Every positive real number has two square roots. Positive Square root of 9 Negative Square root of 9 Positive and negative Square roots of 9

Example 1: •

Example 2: •

Example 3: •

Example 4: •

Example 4: •

Homework • Page 571 (18 -34 even)