Properties of Quadratic Functions in Standard Form Standard

Standard Form of Quadratic Functions • The standard form of a quadratic function is:

Direction of Opening • The value, a, can be used to help us know

Axis of Symmetry • Every parabola has an Axis of Symmetry. • The Axis

VERTEX • The vertex is the most important point on the parabola. • The

The y-intercept • The y-intercept is given to us by the value c. •

Maximum or Minimum • If the parabola opens upward, then its vertex is located

EXAMPLE Consider the given function and determine if it opens upward or downward.

EXAMPLE Consider the given function and determine the equation of the axis of symmetry.

EXAMPLE Consider the given function and determine the coordinates of the vertex. Now, plug

EXAMPLE (Cont. ) Graph the function. Remember symmetry! What is the maximum/minimum value for

Slides: 11

Download presentation

Properties of Quadratic Functions in Standard Form

Standard Form of Quadratic Functions • The standard form of a quadratic function is: • In this form, a can not be zero, meaning there must be a quadratic term. • Make sure that the terms are placed in the proper order with descending powers of x. • In this form, the values a, b, and c can show the properties of the graph of the function.

Direction of Opening • The value, a, can be used to help us know the direction that the parabola opens. • If a is a positive value, then the parabola opens up. • If a is negative, then the parabola opens downward.

Axis of Symmetry • Every parabola has an Axis of Symmetry. • The Axis of Symmetry is a vertical line that passes through the center of the parabola. • Every point on the parabola is mirrored on the opposite side of the Axis of Symmetry. • The equation for the Axis of Symmetry is always:

VERTEX • The vertex is the most important point on the parabola. • The x-coordinate of the vertex is found with: • The y-coordinate is found by plugging the xcoordinate in to the function.

The y-intercept • The y-intercept is given to us by the value c. • This is the point at which the parabola crosses the y-axis. • If we know the vertex and the axis of symmetry, the y-intercept also helps us know a point on the other side of the parabola. • This makes it easy for us to graph the parabola.

Maximum or Minimum • If the parabola opens upward, then its vertex is located at the bottom of it. • In this case, the y-coordinate of the vertex is the MINIMUM value of the function. • If the parabola opens downward, then its vertex is located at the top of it. • In this case, the x-coordinate of the vertex is the MAXIMUM value of the function.

EXAMPLE Consider the given function and determine if it opens upward or downward.

EXAMPLE Consider the given function and determine the equation of the axis of symmetry. Axis of symmetry:

EXAMPLE Consider the given function and determine the coordinates of the vertex. Now, plug this value in for x in the function!

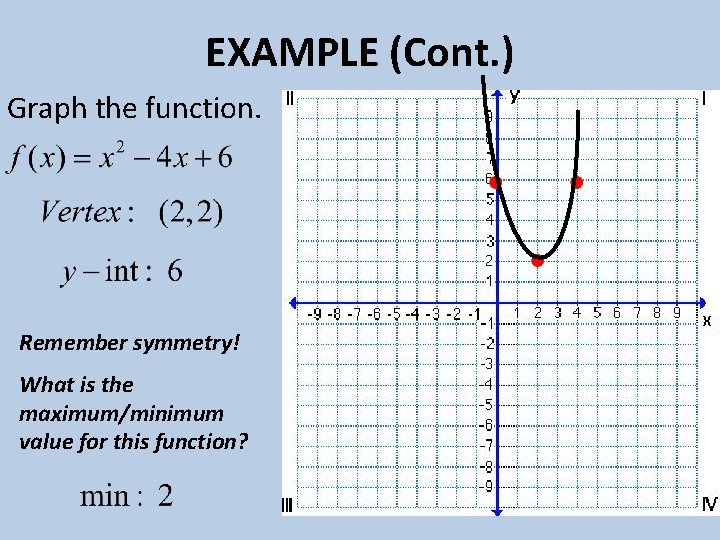
EXAMPLE (Cont. ) Graph the function. Remember symmetry! What is the maximum/minimum value for this function?