Section 5 1 Introduction to Quadratic Functions Quadratic


















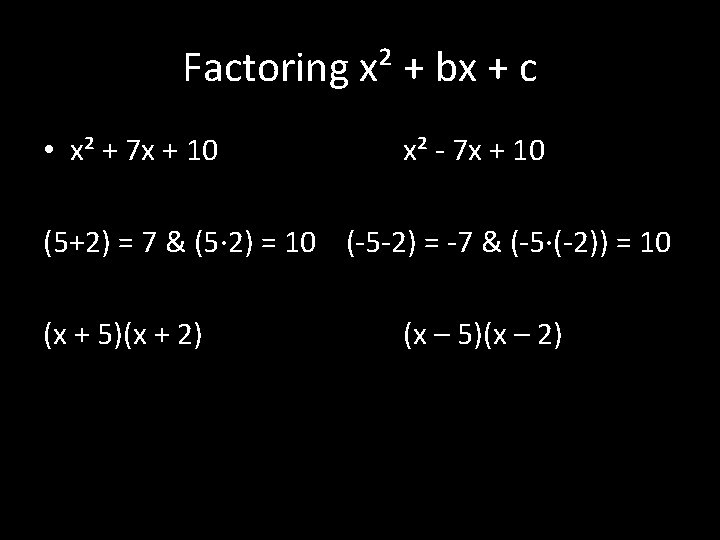










- Slides: 29

Section 5. 1 Introduction to Quadratic Functions

Quadratic Function • A quadratic function is any function that can be written in the form f(x) = ax² + bx + c, where a ≠ 0. • It is defined by a quadratic expression, which is an expression of the form as seen above. • The stopping-distance function, given by: d(x) = ⅟₁₉x² + ¹¹ ₁₀x, is an example of a quadratic function.

Quadratic Functions • Let f(x) = (2 x – 1)(3 x + 5). Show that f represents a quadratic function. Identify a, b, and c. • f(x) = (2 x – 1)(3 x + 5) • f(x) = (2 x – 1)3 x + (2 x – 1)5 • f(x) = 6 x² - 3 x + 10 x – 5 • f(x) = 6 x² + 7 x – 5 a = 6, b = 7, c = - 5

Parabola • The graph of a quadratic function is called a parabola. Parabolas have an axis of symmetry, a line that divides the parabola into two parts that are mirror images of each other. • The vertex of a parabola is either the lowest point on the graph or the highest point on the graph.

Domain and Range of Quadratic Functions • The domain of any quadratic function is the set of all real numbers. • The range is either the set of all real numbers greater than or equal to the minimum value of the function (when the graph opens up). • The range is either the set of all real numbers less than or equal to the maximum value of the function (when the graph opens down).

Minimum and Maximum Values • Let f(x) = ax² + bx + c, where a ≠ 0. The graph of f is a parabola. • If a > 0, the parabola opens up and the vertex is the lowest point. The y-coordinate of the vertex is the minimum value of f. • If a < 0, the parabola opens down and the vertex is the highest point. The y-coordinate of the vertex is the maximum value of f.

Minimum and Maximum Values • f(x) = x² + x – 6 • Because a > 0, the parabola opens up and the function has a minimum value at the vertex. • g(x) = 5 + 4 x - x² • Because a < 0, the parabola opens down and the function has a maximum value at the vertex.

Section 5. 2 Introduction to Solving Quadratic Equations

Solving Equations of the Form x² = a • If x² = a and a ≥ 0, then x = √a or x = - √a, or simply x = ± √a. • The positive square root of a, √a is called the principal square root of a. • Simplify the radical for the exact answer.

Solving Equations of the Form x² = a • Solve 4 x² + 13 = 253 • 4 x² + 13 = 253 - 13 4 x² = 240 Simply the Radical √ 60 = √(2 ∙ 3 ∙ 5) √ 60 = 2√(3 ∙ 5) √ 60 = ± 2√ 15 (exact answer) 4 x² = 240 4 4 x² = 60 x = √ 60 or x = - √ 60 (exact answer) x = 7. 75 or x = - 7. 75 (approximate answer)

Properties of Square Roots • Product Property of Square Roots: • If a ≥ 0 and b ≥ 0: √(ab) = √a ∙ √b • Quotient Property of Square Roots: • If a ≥ 0 and b > 0: √(a/b) = √(a) ÷ √(b)

Properties of Square Roots • Solve 9(x – 2)² = 121 • 9(x – 2)² = 121 9 9 (x – 2)² = 121/9 √(x – 2)² = ±√(121/9) x – 2 = ±√(121/9) x– 2 +2 = √(121/9) +2 x = 2 + √(121/9) or 2 - √(121/9) x = 2 + [√(121) / √ (9)] or 2 – [√(121) / √(9)] x = 2 + (11/3) or 2 – (11/3) x = 17/3 or x = - 5/3

Pythagorean Theorem • If ∆ABC is a right triangle with the right angle at C, then a² + b² = c² A c a C B b

Pythagorean Theorem • If ∆ABC is a right triangle with the right angle at C, then a² + b² = c² A c 2. 5 C B 5. 1 2. 5² + 5. 1² = c² 6. 25 + 26. 01 = c² 32. 26 = c² √(32. 26) = c 5. 68 = c

Section 5. 3 Factoring Quadratic Expressions

Factoring Quadratic Expressions • When you learned to multiply two expressions like 2 x and x + 3, you learned how to write a product as a sum. • Factoring reverses the process, allowing you to write a sum as a product. • To factor an expression containing two or more terms, factor out the greatest common factor (GCF) of the two expressions.

Factoring Quadratic Expressions • • • 3 a² - 12 a 3 a² = 3 a ∙ a 12 a = 3 a ∙ 4 The GCF = 3 a 3 a(a) – 3 a ∙ 4 (3 a)(a – 4) 3 x(4 x + 5) – 5(4 x + 5) The GCF = 4 x + 5 (3 x – 5)(4 x +5)

Factoring x² + bx + c • To factor an expression of the form: • ax² + bx + c where a = 1, look for integers r and s such that r ∙ s = c and r + s = b. • Then factor the expression. • x² + bx + c = (x + r)(x + s)
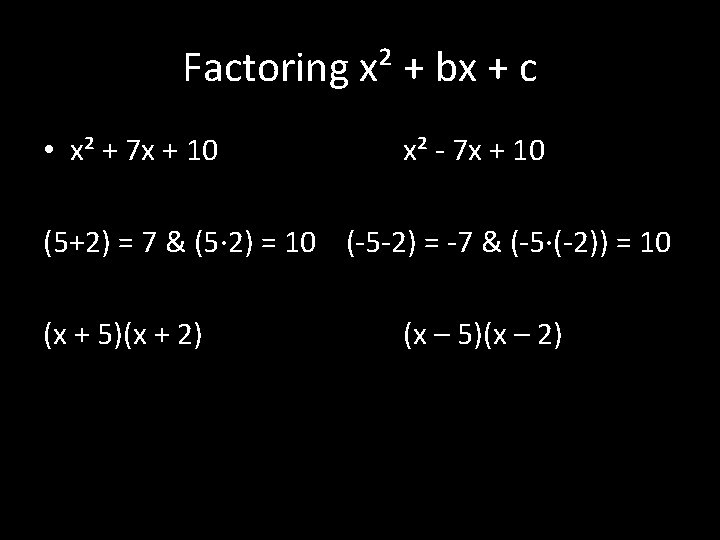

Factoring the Difference of Two Squares • • • a² - b² = (a + b)(a – b) (x + 3)(x – 3) x² + 3 x - 9 x² - 3²

Factoring Perfect-Square Trinomials a² + 2 ab + b² = (a + b)² (x + 3)(x + 3) x² + 3 x + 9 X² +2(3 x) + 9 a² - 2 ab + b² = (a – b)² (x – 3)(x – 3) x² - 3 x – 3 x + 9 x² - 2(3 x) + 9

Zero-Product Property • If pq = 0, then p = 0 or q = 0. • • 2 x² - 11 x = 0 x(2 x – 11) = 0 (Factor out an x) x = 0 or 2 x – 11 = 0 x = 11 or x = 11/2

Section 5. 4 Completing the Square

Completing the Square • When a quadratic equation does not contain a perfect square, you an create a perfect square in the equation by completing the square. • Completing the square is a process by which you can force a quadratic expression to factor.

Specific Case of a Perfect-Square Trinomial • x² + 8 x + 16 = (x + 4)² • Understand: (½)8 = 4 → 4² = 16

Examples of Completing the Square • • • x² - 6 x (½)(-6) = -3 (-3)² → = 9 The perfect-square x² - 6 x + 9 = (x – 3)² x² + 15 x (½)(15) = (15/2)² → = (15/2)² The perfect square x² + 15 x + (15/2)² = [x + (15/2)]²

Solving a Quadratic Equation by Completing the Square • • x² + 10 x – 24 = 0 + 24 +24 x² +10 x = 24 x²+10 x+(5)²=24+(5)² x² + 10 x + 25 = 49 (x + 5)² = 49 x+5=± 7 x = - 12 or x = 2 2 x² + 6 x = 7 2(x² + 3 x) = 7 x² + 3 x = (7/2) x²+3 x+(3/2)²=(7/2)+(3/2)² x²+3 x+(3/2)² =(7/2)+(9/4) [x + (3/2)]² = (23/4) x + (3/2) = ±√(23/4) x = - (3/2) + √(23/4) (0. 90) X = - (3/2) - √(23/4) (-3. 90)

Vertex Form • If the coordinates of the vertex of the graph of y = ax² + bx + c, where a ≠ 0, are (h, k), then you can represent the parabola as: • y = a(x – h)² + k, which is the vertex form of a quadratic function.

Vertex Form • • • Given g(x) = 2 x² + 12 x + 13 2(x² + 6 x) + 13 2(x² + 6 x + 9) + 13 – 2(9) 2(x + 3)² - 5 2[x – (-3)]² + (- 5) (Vertex Form) The coordinates (h, k) of the vertex are (-3, -5) and the equation for the axis of symmetry is x = - 3.