Section 4 1 Notes Graphing Quadratic Functions Quadratic
















- Slides: 22

Section 4. 1 Notes: Graphing Quadratic Functions

Quadratic Function: Characteristics *Greatest exponent is 2. *Its graph is called a parabola. f(x) = ax 2 + bx + c, where a ≠ 0 Quadratic Term Linear Term Constant Term

Example 1: Graph f(x) = x 2 + 3 x – 1 by making a table of values x x 2 + 3 x – 1 f(x) (x, y)

The axis of symmetry is a line through the graph of a parabola that divides the graph into two congruent halves. Each side of the parabola is a reflection of the other side. The axis of symmetry will intersect a parabola at only one point, called the vertex.

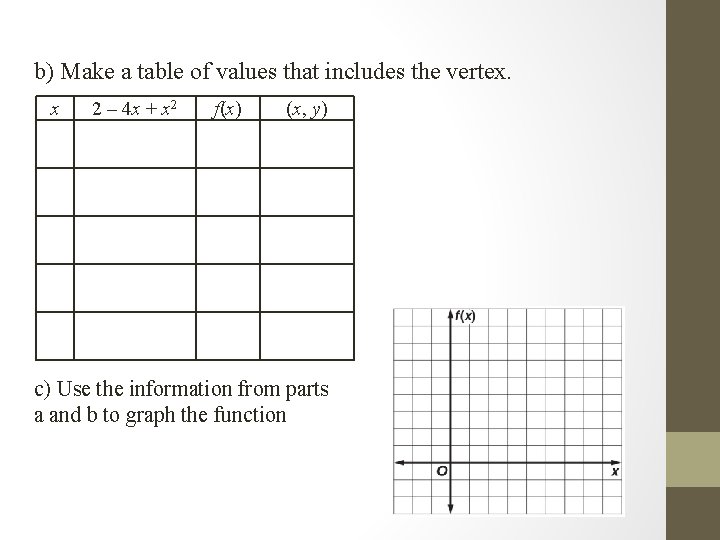
Example 2: a) Consider the quadratic function f(x) = 2 – 4 x + x 2. Find the yintercept, the equation of the axis of symmetry, and the x-coordinate of the vertex.

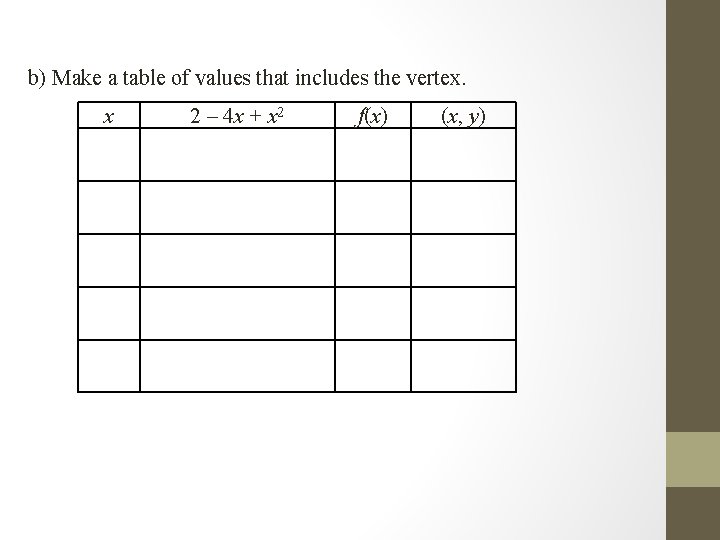
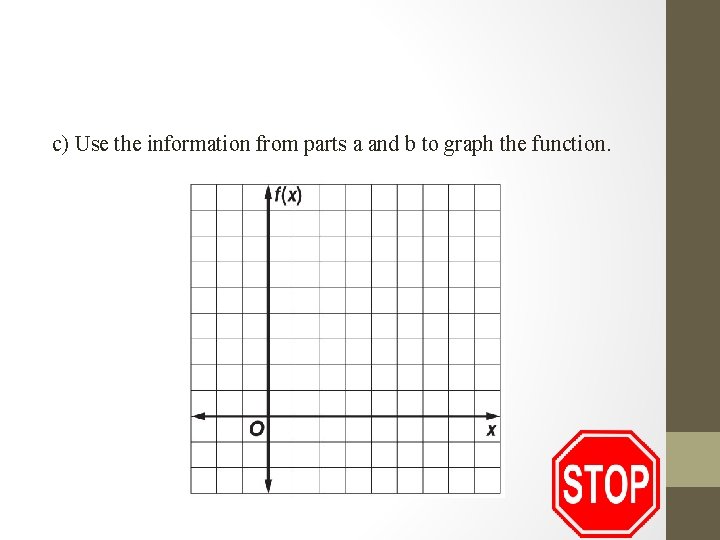
b) Make a table of values that includes the vertex. x 2 – 4 x + x 2 f(x) (x, y) c) Use the information from parts a and b to graph the function

You Try! a) Consider the quadratic function f(x) = x 2 + 6 x + 8. Find the yintercept, the equation of the axis of symmetry, and the x-coordinate of the vertex.

b) Make a table of values that includes the vertex. x 2 – 4 x + x 2 f(x) (x, y)

c) Use the information from parts a and b to graph the function.

Vertex Form: y = a(x – h)2 + k, where (h, k) is the vertex, x = h is the axis of symmetry, and a determines the shape of the parabola and the direction in which it opens.

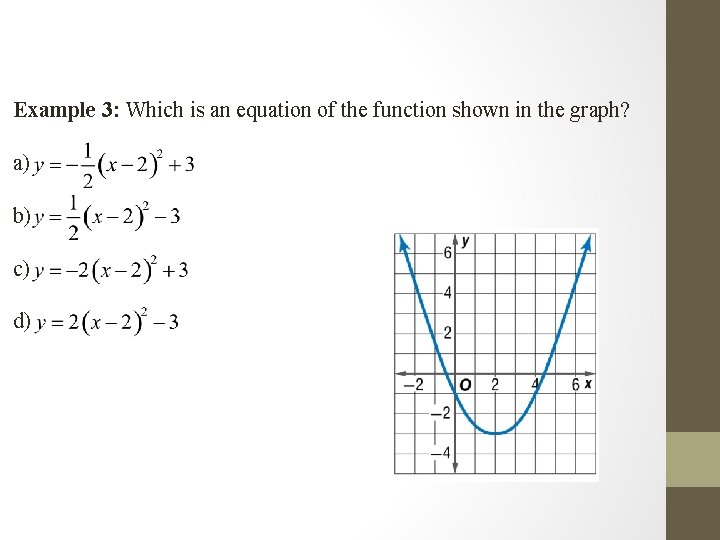
Example 3: Which is an equation of the function shown in the graph? a) b) c) d)

Example 4: Graph y = – 2(x – 1)2 + 3

Example 5: Graph y = 3(x – 2)2 – 4 a) b) c) d)

The y-coordinate of the vertex of a quadratic function is the maximum value or the minimum value of the function. These values represent the greatest or lowest possible value of the function can reach.

Domain and Range of Quadratics The domain of a quadratic function will always be all real numbers. The range will either be: • all real numbers less than or equal to the maximum • all real numbers greater than or equal to the minimum.

Example 6: Consider the function f(x) = –x 2 + 2 x + 3. a) Determine whether the function has a maximum or minimum value. b) State the maximum or minimum value of the function. c) State the domain and range of the function

You Try! Consider the function f(x) = x 2 + 4 x + 4. a) Determine whether the function has a maximum or minimum value. b) State the maximum or minimum value of the function. c) State the domain and range of the function

Example 7: The path of a diver is approximated by feet in the figure shown and the equation given. What is the maximum height of the diver? Approximately how long did it take the diver to reach his maximum height?

Example 8: a) A souvenir shop sells about 200 coffee mugs each month for $6 each. The shop owner estimates that for each $0. 50 increase in the price, he will sell about 10 fewer coffee mugs per month. How much should the owner charge for each mug in order to maximize the monthly income from their sales? Words Income equals number of mugs times price. Variable Let x = the number of $0. 50 price increases. Let I(x) equal the income as a function of x. SKIP

Example 9: The Empire State Building is 1250 feet tall. If an object is thrown upward from the top of the building at an initial velocity of 38 feet per second, its height s seconds after it is thrown is given by the function h(s) = – 16 s 2 + 38 s + 1250. How high does the ball go in the air?

Example 10: A juggler throws a ball in the air, releasing it 5 feet above the ground with an initial velocity of 15 ft/sec. She catches the ball with her other hand when the ball returns to 5 feet above the ground. If the equation h(t) = – 16 t 2 + 15 t give the path of the ball from hand to hand, find how height the ball gets in the air.

Example 11: A firework is shot upward so that it follows the equation y = – 16 x 2 + 80 x + 3 where y is the height of the firework and x is time. How high does the firework climb before it starts to descend?