Digital Lesson Graphing Quadratic Functions Graphing Quadratic Functions

Digital Lesson Graphing Quadratic Functions

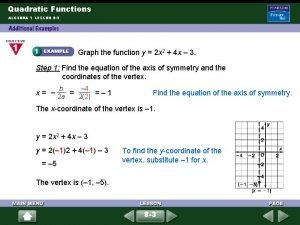
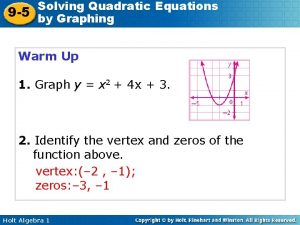
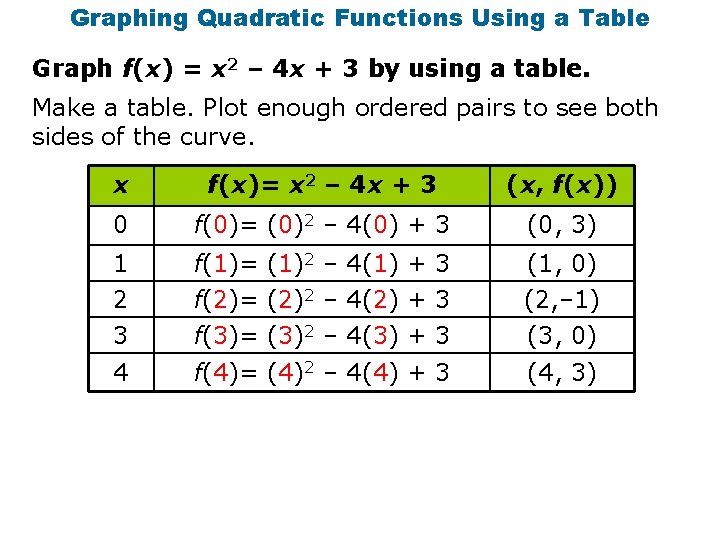
Graphing Quadratic Functions Using a Table Graph f(x) = x 2 – 4 x + 3 by using a table. Make a table. Plot enough ordered pairs to see both sides of the curve. x f(x)= x 2 – 4 x + 3 (x, f(x)) 0 f(0)= (0)2 – 4(0) + 3 (0, 3) 1 2 f(1)= (1)2 – 4(1) + 3 f(2)= (2)2 – 4(2) + 3 (1, 0) (2, – 1) 3 f(3)= (3)2 – 4(3) + 3 (3, 0) 4 f(4)= (4)2 – 4(4) + 3 (4, 3)

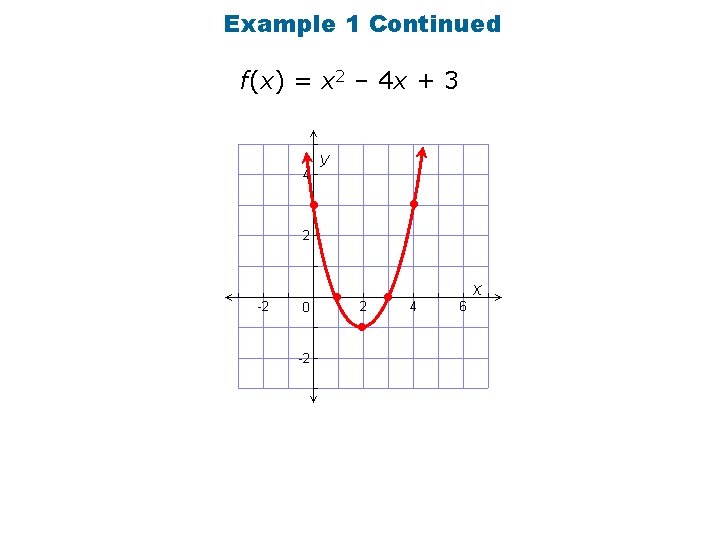
Example 1 Continued f(x) = x 2 – 4 x + 3 • • •

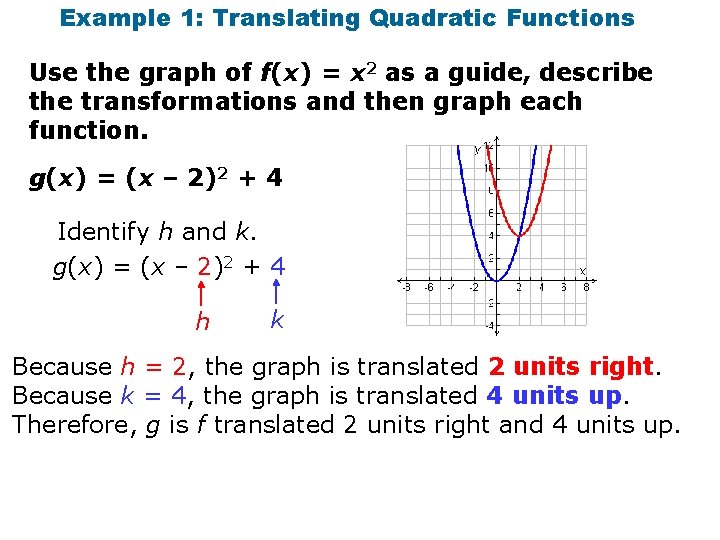
Example 1: Translating Quadratic Functions Use the graph of f(x) = x 2 as a guide, describe the transformations and then graph each function. g(x) = (x – 2)2 + 4 Identify h and k. g(x) = (x – 2)2 + 4 h k Because h = 2, the graph is translated 2 units right. Because k = 4, the graph is translated 4 units up. Therefore, g is f translated 2 units right and 4 units up.

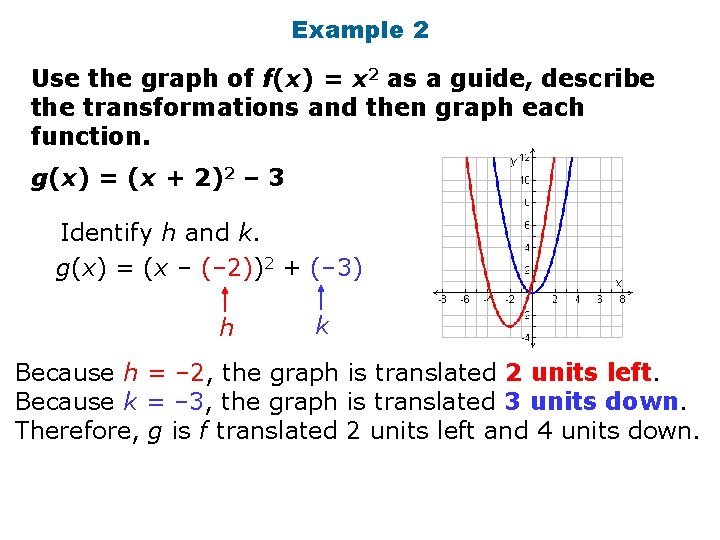
Example 2 Use the graph of f(x) = x 2 as a guide, describe the transformations and then graph each function. g(x) = (x + 2)2 – 3 Identify h and k. g(x) = (x – (– 2))2 + (– 3) h k Because h = – 2, the graph is translated 2 units left. Because k = – 3, the graph is translated 3 units down. Therefore, g is f translated 2 units left and 4 units down.

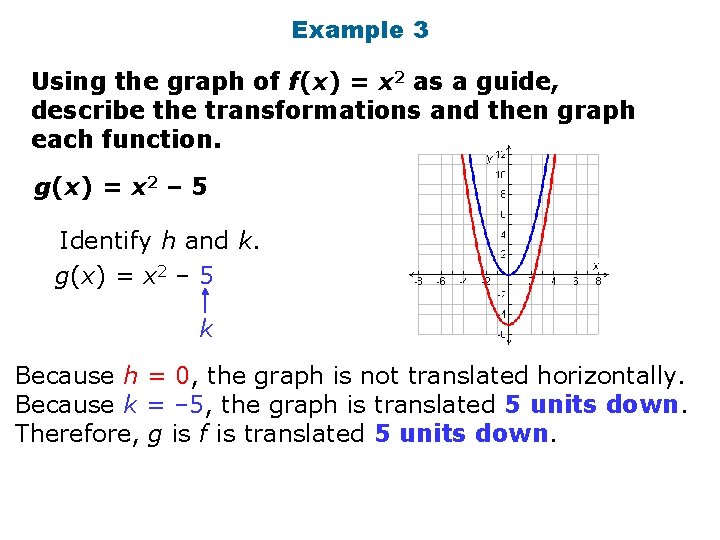
Example 3 Using the graph of f(x) = x 2 as a guide, describe the transformations and then graph each function. g(x) = x 2 – 5 Identify h and k. g(x) = x 2 – 5 k Because h = 0, the graph is not translated horizontally. Because k = – 5, the graph is translated 5 units down. Therefore, g is f is translated 5 units down.

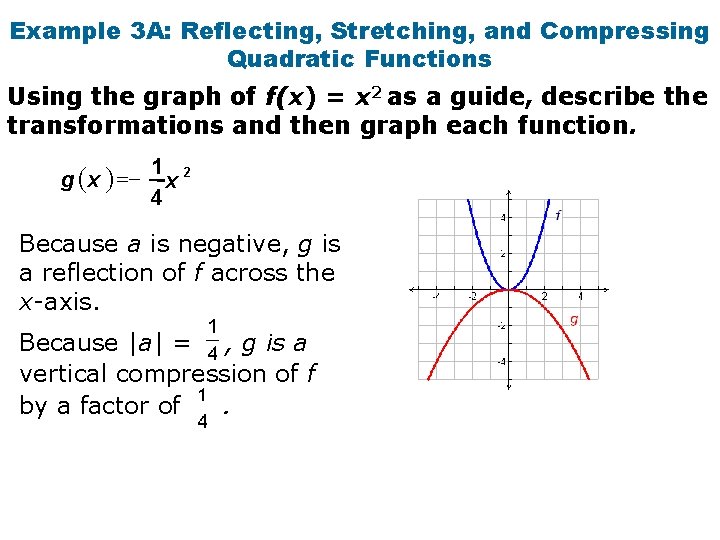
Example 3 A: Reflecting, Stretching, and Compressing Quadratic Functions Using the graph of f(x) = x 2 as a guide, describe the transformations and then graph each function. g (x ) =- 1 x 4 2 Because a is negative, g is a reflection of f across the x-axis. Because |a| = , g is a vertical compression of f by a factor of.

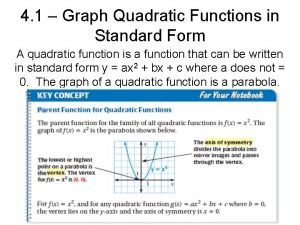
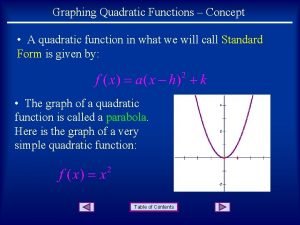
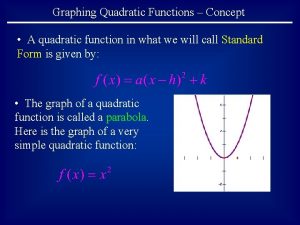
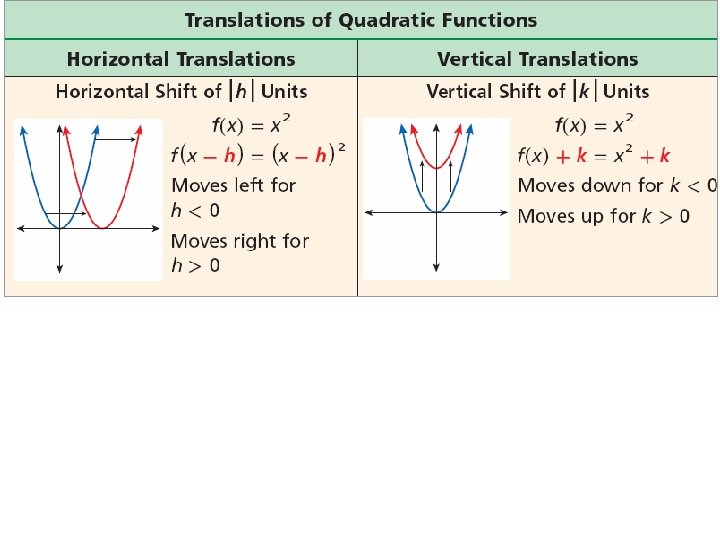
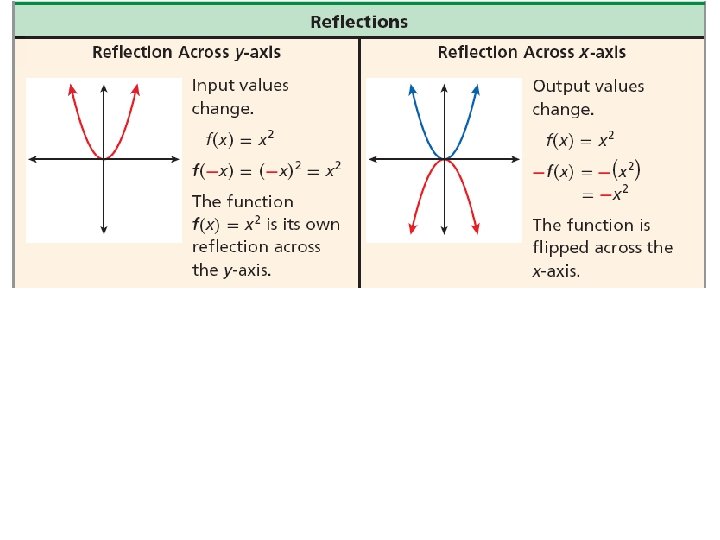
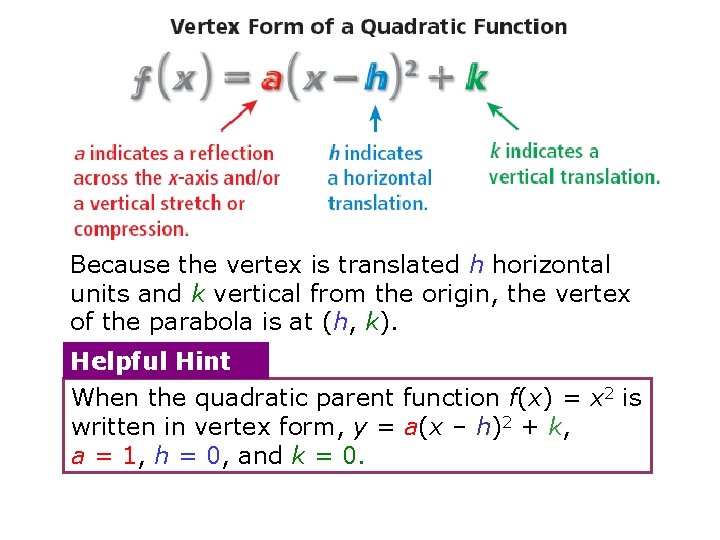
If a parabola opens upward, it has a lowest point. If a parabola opens downward, it has a highest point. This lowest or highest point is the vertex of the parabola. The parent function f(x) = x 2 has its vertex at the origin. You can identify the vertex of other quadratic functions by analyzing the function in vertex form. The vertex form of a quadratic function is f(x) = a(x – h)2 + k, where a, h, and k are constants.

Because the vertex is translated h horizontal units and k vertical from the origin, the vertex of the parabola is at (h, k). Helpful Hint When the quadratic parent function f(x) = x 2 is written in vertex form, y = a(x – h)2 + k, a = 1, h = 0, and k = 0.

Example 4: Writing Transformed Quadratic Functions Use the description to write the quadratic function in vertex form. The parent function f(x) = x 2 is vertically stretched by a factor of and then translated 2 units left and 5 units down to create g. Step 1 Identify how each transformation affects the constant in vertex form. Vertical stretch by 4 4 = : a 3 3 Translation 2 units left: h = – 2 Translation 5 units down: k = – 5

Example 4: Writing Transformed Quadratic Functions Step 2 Write the transformed function. g(x) = a(x – h)2 + k Vertex form of a quadratic function = (x – (– 2))2 + (– 5) Substitute = (x + 2)2 – 5 g(x) = (x + 2)2 – 5 Simplify. for a, – 2 for h, and – 5 for k

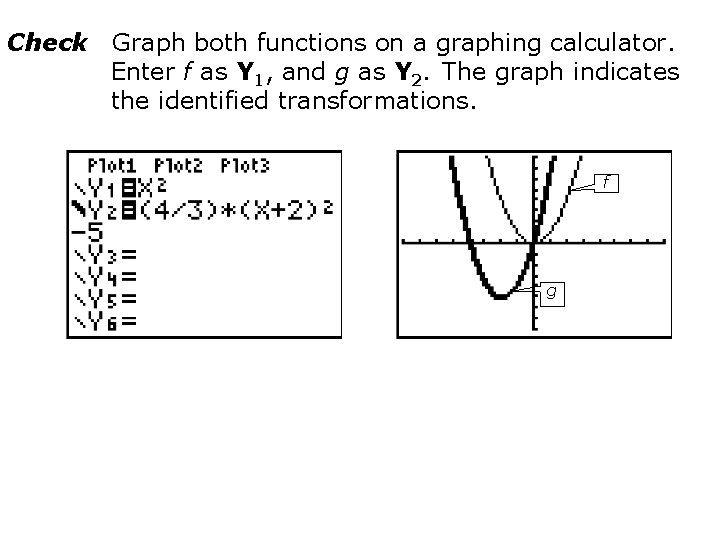
Check Graph both functions on a graphing calculator. Enter f as Y 1, and g as Y 2. The graph indicates the identified transformations. f g

Check It Out! Example 4 a Use the description to write the quadratic function in vertex form. The parent function f(x) = x 2 is vertically compressed by a factor of and then translated 2 units right and 4 units down to create g. Step 1 Identify how each transformation affects the constant in vertex form. Vertical compression by : a= Translation 2 units right: h = 2 Translation 4 units down: k = – 4

Check It Out! Example 4 a Continued Step 2 Write the transformed function. g(x) = a(x – h)2 + k Vertex form of a quadratic function = (x – 2)2 + (– 4) Substitute = (x – 2)2 – 4 g(x) = (x – 2)2 – 4 Simplify. for a, 2 for h, and – 4 for k.

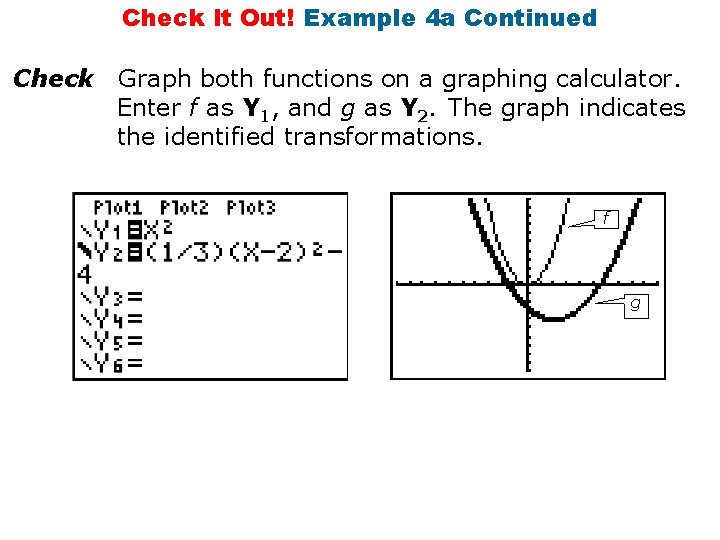
Check It Out! Example 4 a Continued Check Graph both functions on a graphing calculator. Enter f as Y 1, and g as Y 2. The graph indicates the identified transformations. f g

Example The parent function f(x) = x 2 is vertically stretched by a factor of 3 and translated 4 units right and 2 units up to create g. Write g in vertex form. g(x) = 3(x – 4)2 + 2

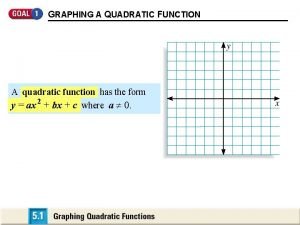
Let a, b, and c be real numbers a 0. The function f (x) = ax 2 + bx + c is called a quadratic function. The graph of a quadratic function is a parabola. Every parabola is symmetrical about a line called the axis (of symmetry). y The intersection point of the parabola and the axis is called the vertex of the parabola. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. f (x) = ax 2 + bx + c vertex x axis 19

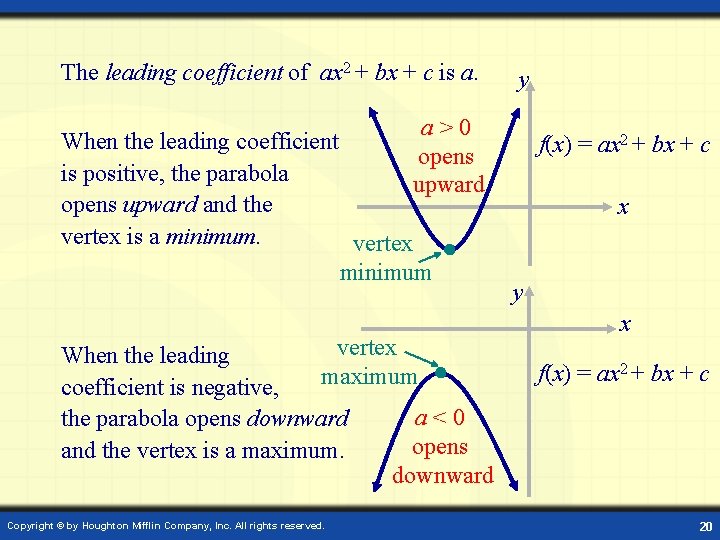
The leading coefficient of ax 2 + bx + c is a. y a>0 opens upward When the leading coefficient is positive, the parabola opens upward and the vertex is a minimum. vertex minimum vertex When the leading maximum coefficient is negative, a<0 the parabola opens downward opens and the vertex is a maximum. downward Copyright © by Houghton Mifflin Company, Inc. All rights reserved. f(x) = ax 2 + bx + c x y x f(x) = ax 2 + bx + c 20

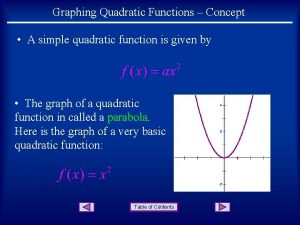
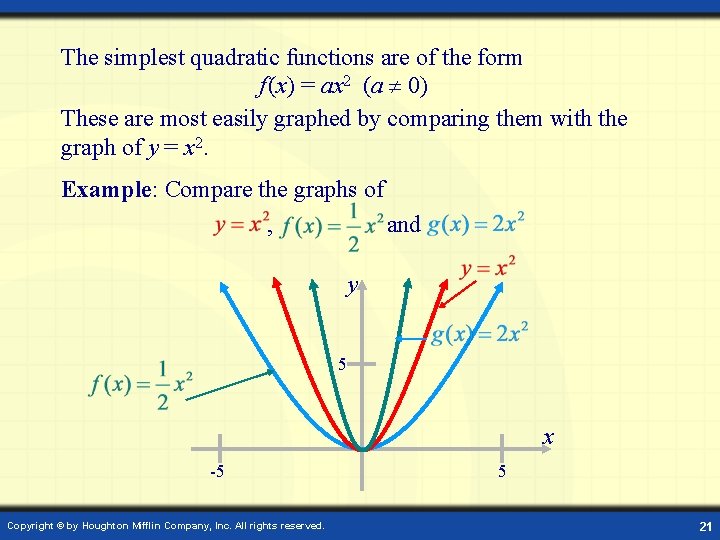
The simplest quadratic functions are of the form f (x) = ax 2 (a 0) These are most easily graphed by comparing them with the graph of y = x 2. Example: Compare the graphs of , and y 5 x -5 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5 21

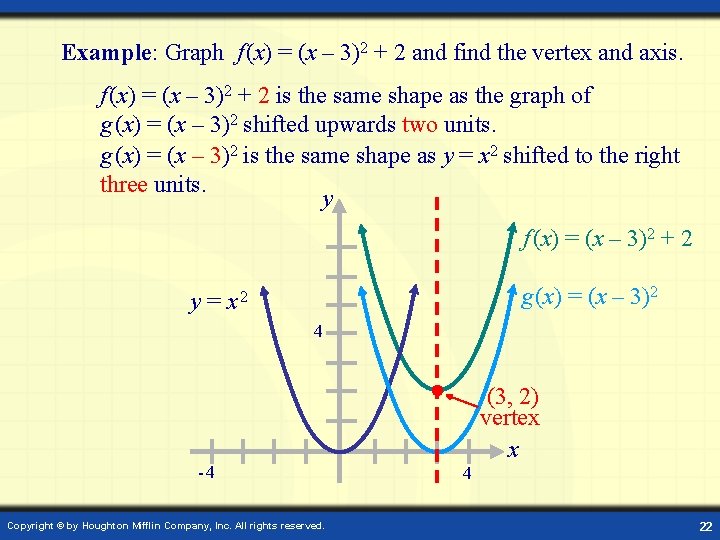
Example: Graph f (x) = (x – 3)2 + 2 and find the vertex and axis. f (x) = (x – 3)2 + 2 is the same shape as the graph of g (x) = (x – 3)2 shifted upwards two units. g (x) = (x – 3)2 is the same shape as y = x 2 shifted to the right three units. y f (x) = (x – 3)2 + 2 g (x) = (x – 3)2 y = x 2 4 -4 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. (3, 2) vertex x 4 22

Vertex of a Parabola The vertex of the graph of f (x) = ax 2 + bx + c (a 0) Example: Find the vertex of the graph of f (x) = x 2 – 10 x + 22 original equation a = 1, b = – 10, c = 22 At the vertex, So, the vertex is (5, -3). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 23

Example: A basketball is thrown from the free throw line from a height of six feet. What is the maximum height of the ball if the path of the ball is: The path is a parabola opening downward. The maximum height occurs at the vertex. At the vertex, So, the vertex is (9, 15). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 24

Example: A fence is to be built to form a rectangular corral along the side of a barn 65 feet long. If 120 feet of fencing are available, what are the dimensions of the corral of maximum area? barn x corral x 120 – 2 x Let x represent the width of the corral and 120 – 2 x the length. Area = A(x) = (120 – 2 x) x = – 2 x 2 + 120 x The graph is a parabola and opens downward. The maximum occurs at the vertex where a = – 2 and b = 120 – 2 x = 120 – 2(30) = 60 The maximum area occurs when the width is 30 feet and the length is 60 feet. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 25

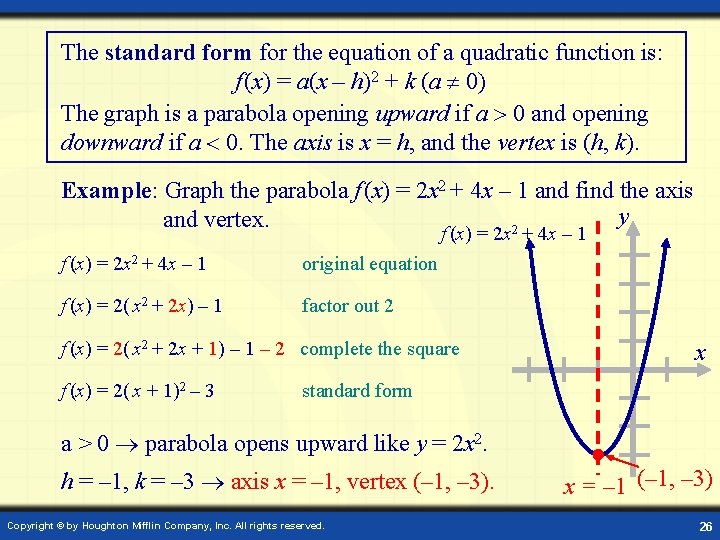
The standard form for the equation of a quadratic function is: f (x) = a(x – h)2 + k (a 0) The graph is a parabola opening upward if a 0 and opening downward if a 0. The axis is x = h, and the vertex is (h, k). Example: Graph the parabola f (x) = 2 x 2 + 4 x – 1 and find the axis y and vertex. 2 f (x) = 2 x + 4 x – 1 f (x) = 2 x 2 + 4 x – 1 original equation f (x) = 2( x 2 + 2 x) – 1 factor out 2 f (x) = 2( x 2 + 2 x + 1) – 1 – 2 complete the square f (x) = 2( x + 1)2 – 3 x standard form a > 0 parabola opens upward like y = 2 x 2. h = – 1, k = – 3 axis x = – 1, vertex (– 1, – 3). Copyright © by Houghton Mifflin Company, Inc. All rights reserved. x = – 1 (– 1, – 3) 26

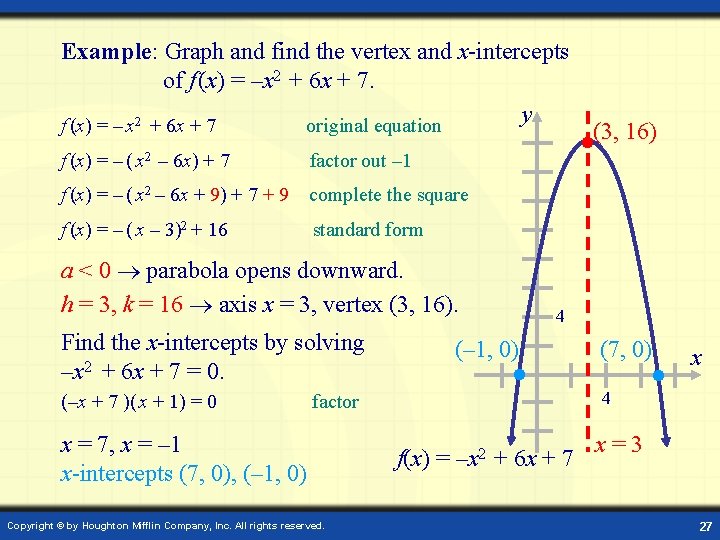
Example: Graph and find the vertex and x-intercepts of f (x) = –x 2 + 6 x + 7. y f (x) = – x 2 + 6 x + 7 original equation f (x) = – ( x 2 – 6 x) + 7 factor out – 1 f (x) = – ( x 2 – 6 x + 9) + 7 + 9 complete the square f (x) = – ( x – 3)2 + 16 standard form a < 0 parabola opens downward. h = 3, k = 16 axis x = 3, vertex (3, 16). Find the x-intercepts by solving –x 2 + 6 x + 7 = 0. (–x + 7 )( x + 1) = 0 4 (– 1, 0) Copyright © by Houghton Mifflin Company, Inc. All rights reserved. (7, 0) x 4 factor x = 7, x = – 1 x-intercepts (7, 0), (– 1, 0) (3, 16) f(x) = –x 2 + 6 x + 7 x=3 27

Vertex Form of a Quadratic • f(x) = a(x – h)2 + k Where (h, k) is the vertex. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 28

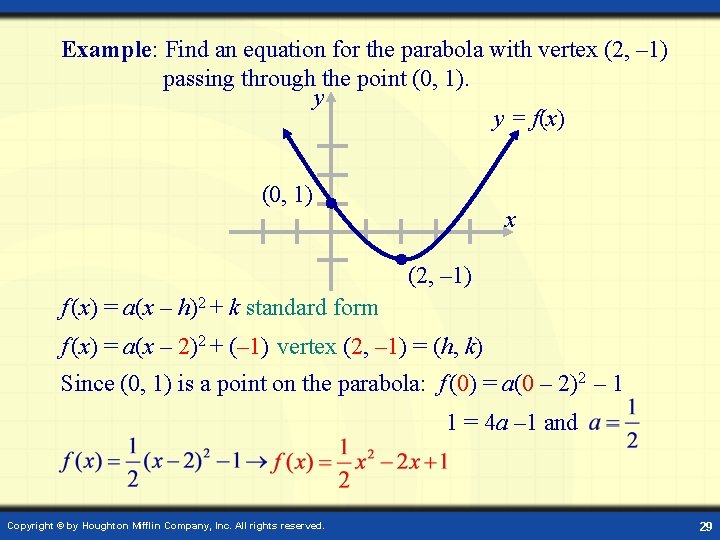
Example: Find an equation for the parabola with vertex (2, – 1) passing through the point (0, 1). y y = f(x) (0, 1) x (2, – 1) f (x) = a(x – h)2 + k standard form f (x) = a(x – 2)2 + (– 1) vertex (2, – 1) = (h, k) Since (0, 1) is a point on the parabola: f (0) = a(0 – 2)2 – 1 1 = 4 a – 1 and Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 29