Exploring Quadratic Functions Quadratic functions around you Quadratic

“Exploring Quadratic Functions”

Quadratic functions around you

Quadratic Functions (what you need to know…. you’ll come across them again and again): l l Functions with the form y=ax 2+bx+c are called quadratic functions and their graphs have a parabolic shape When we solve ax 2+bx+c=0 we look for values of x that are x-intercepts (because we have y=0) The x-intercepts are called the solutions or roots of a quadratic equation A quadratic equation can have two real solutions, one real solution, or no real solutions

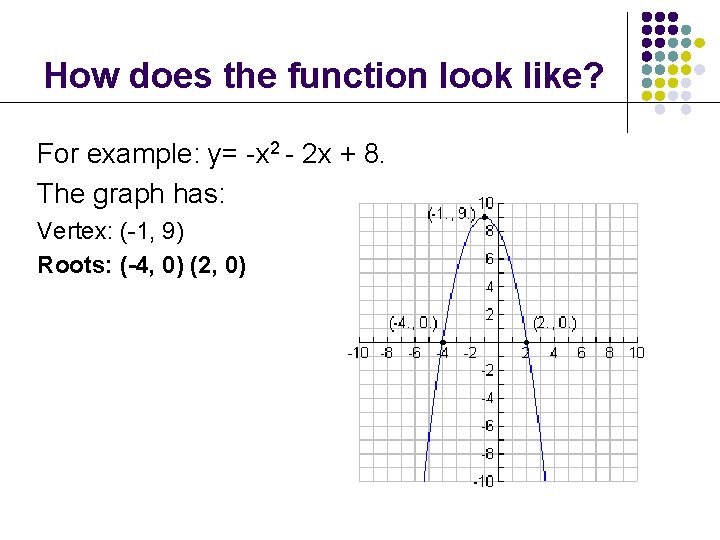
How does the function look like? For example: y= -x 2 - 2 x + 8. The graph has: Vertex: (-1, 9) Roots: (-4, 0) (2, 0)

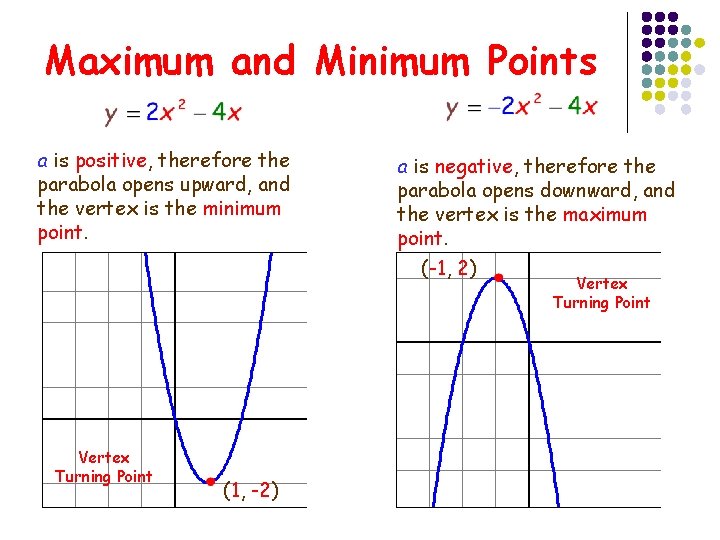
Maximum and Minimum Points a is positive, therefore the parabola opens upward, and the vertex is the minimum point. a is negative, therefore the parabola opens downward, and the vertex is the maximum point. (-1, 2) Vertex Turning Point (1, -2) Vertex Turning Point

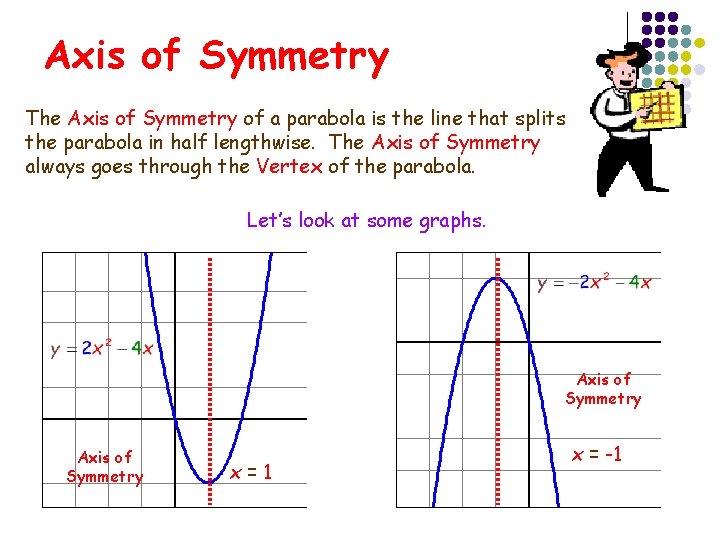
Axis of Symmetry The Axis of Symmetry of a parabola is the line that splits the parabola in half lengthwise. The Axis of Symmetry always goes through the Vertex of the parabola. Let’s look at some graphs. Axis of Symmetry x=1 x = -1

Finding the Axis of Symmetry & Vertex You can find the Axis of Symmetry of any quadratic equation by using the formula Let’s take a look at those equations again. a = 2, b = -4, c = 0 vertex (1, -2) To find the coordinates of the vertex, plug the value of x into the original function. a = -2, b = -4, c = 0 vertex (-1, 2)

Quadratic Functions Forms l Function: l Vertex Form: (standard form)

Let’s review what you have learnt. Show that g represents a quadratic function. Identify a, b, and c.

Let’s take a look at the graph. “Parts of a Parabola” l Axis of Symmetry (Line of Symmetry) LOS: The line that divides the parabola into two parts that are mirror images of each other. l Vertex: Either the lowest (minimum) or highest (maximum) point.

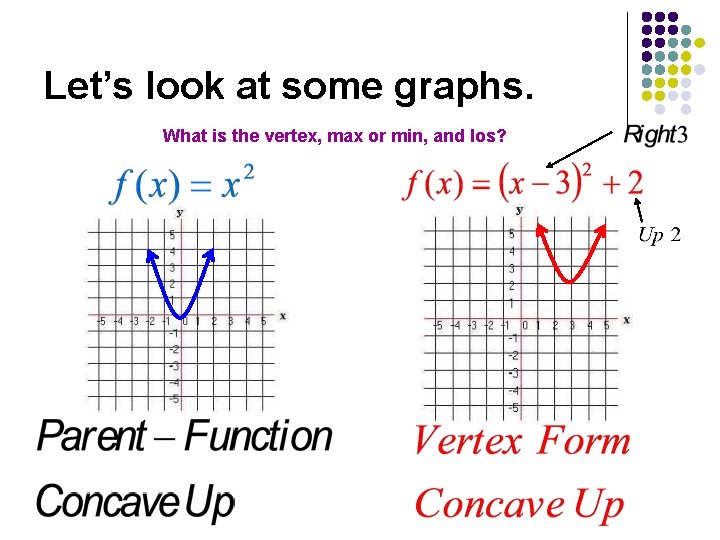
Let’s look at some graphs. What is the vertex, max or min, and los?

Desmos

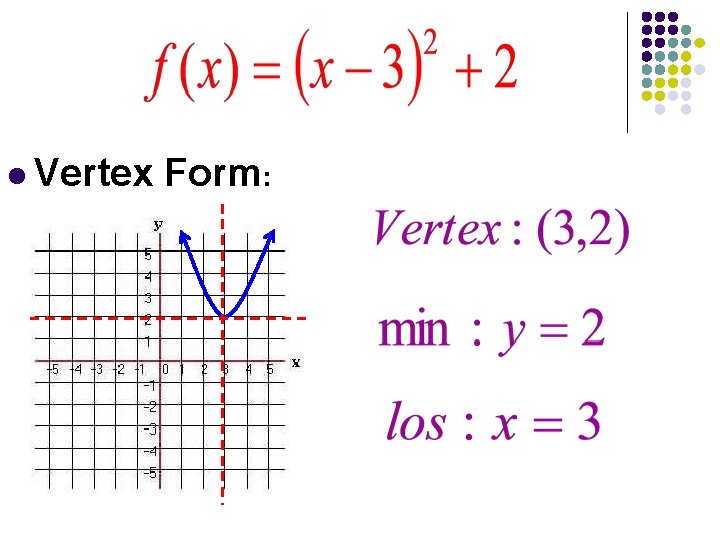
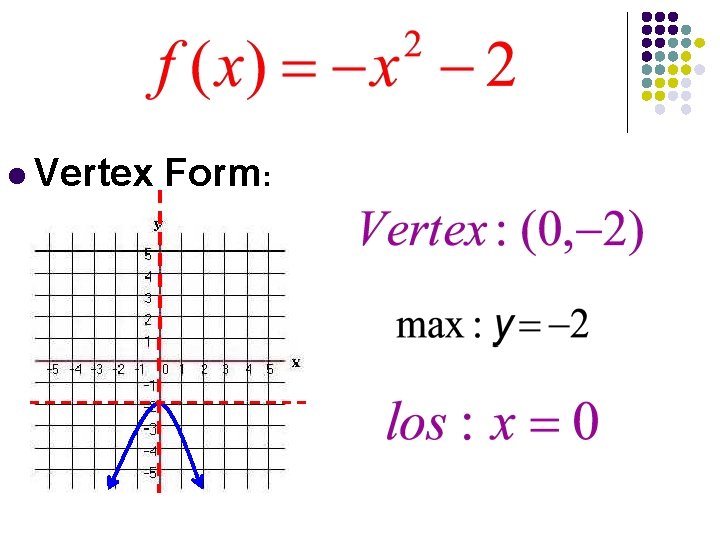
l Vertex Form:

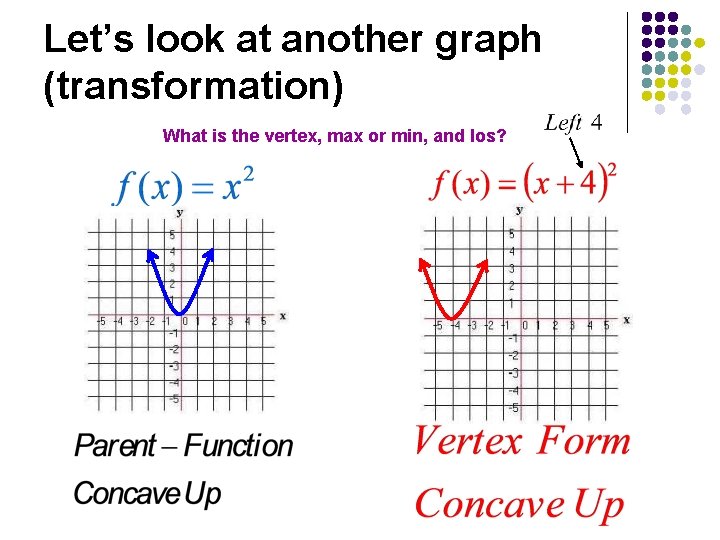
Let’s look at another graph (transformation) What is the vertex, max or min, and los?

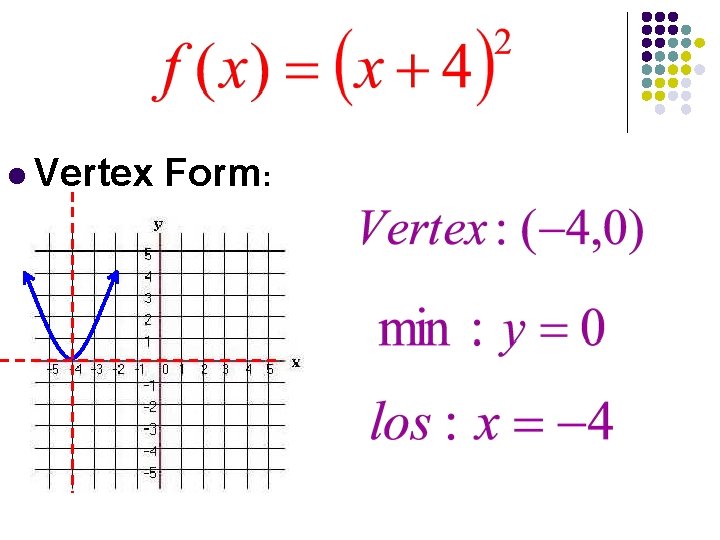
l Vertex Form:

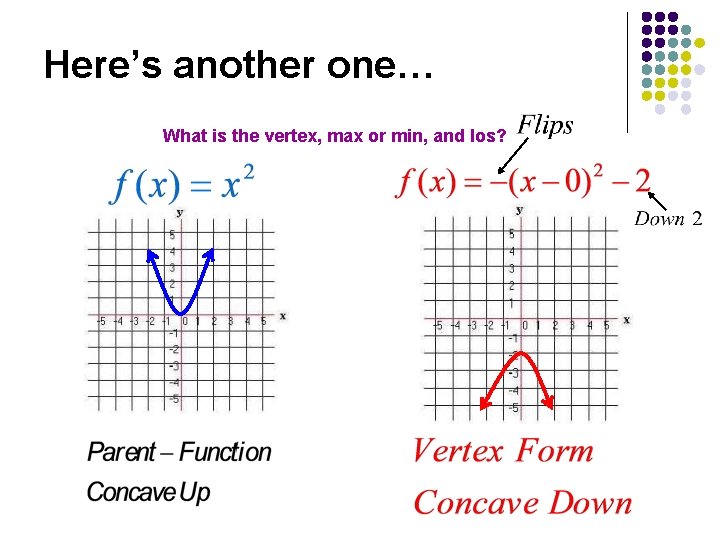
Here’s another one… What is the vertex, max or min, and los?

l Vertex Form:

Solving Quadratic Functions

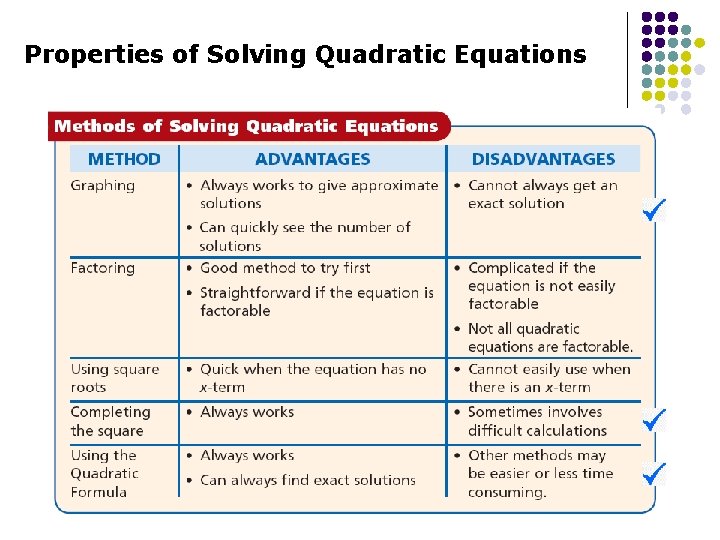
Properties of Solving Quadratic Equations

…by Completing the Square l

The Aim of Completing the Square … is to write a quadratic function as a perfect square. Here are some examples of perfect squares! x 2 + 6 x + 9 l x 2 - 10 x + 25 l x 2 + 12 x + 36 l Try to factor these (they’re easy).

Perfect Square Trinomials l x 2 =(x+3)2 + 6 x + 9 2 2 =(x-5) l x - 10 x + 25 l x 2 + 12 x + 36 =(x+6)2 Can you see a numerical connection between … 6 and 9 using 3 -10 and 25 using -5 12 and 36 using 6

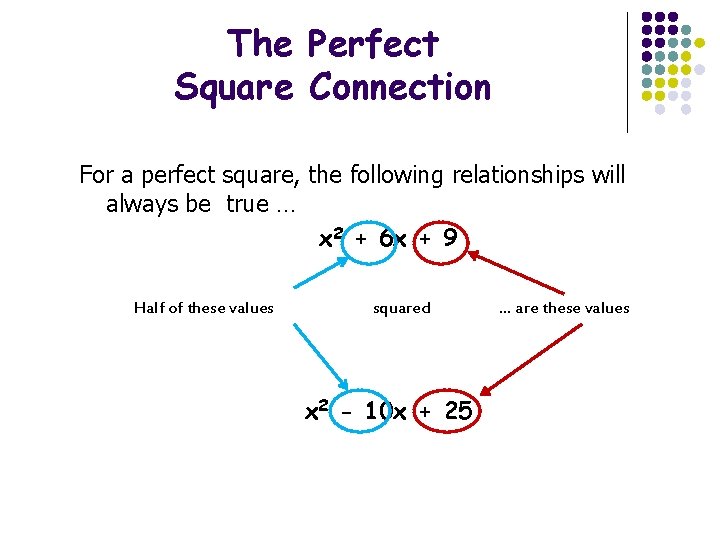
The Perfect Square Connection For a perfect square, the following relationships will always be true … x 2 + 6 x + 9 Half of these values squared x 2 - 10 x + 25 … are these values

Perfect Square Trinomials Create perfect square trinomials. l x 2 + 20 x + ___ 100 l x 2 - 4 x + ___ 4 l x 2 + 5 x + ___ 25/4 l

…by Completing the Square Solve the following equation by completing the square: Step 1: Move the constant term (i. e. the number) just a li…. ittle bit further to right x 2 + 8 x -20 = 0

…by Completing the Square Step 2: Find the term that completes the square. Add that term to the expression. Step 3: Put the opposite sign of the term found in step 2. Step 4: Factor and simplify the expression. x 2 + 8 x + (½(8))2 -20 = 0 x 2 + 8 x + 16 -20 = 0 - 16 -20 = 0 (x + 4)2 - 36 = 0

…by Completing the Square Step 5: Solve for x. (x + 4)2 - 36 = 0 (x + 4)2 = 36 x+4= 6 x = -4 - 6 or x = -4 + 6 x = -10 or x = 2 Solving is a simple process …