Graphing Quadratic Functions in Standard Form y ax

Quadratic Functions y The graph of a quadratic function is a parabola. Vertex (Maximum)

Standard Form y The standard form of a quadratic function is a>0 y =

Line of Symmetry Parabolas have a symmetric property to them. Lineyof Symmetry If we

Finding the Line of Symmetry When a quadratic function is in standard form y

Finding the Vertex We know the line of symmetry always goes through the vertex.

A Quadratic Function in Standard Form The standard form of a quadratic function is

A Quadratic Function in Standard Form Example 1 y a. Graph b. Find and

A Quadratic Function in Standard Form Example 2 a. Graph b. Find and label

A Quadratic Function in Standard Form Example 3 a. Graph b. Find and label

Slides: 10

Download presentation

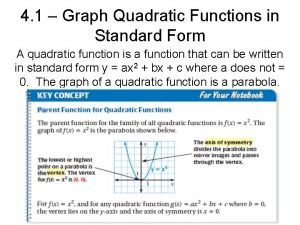
Graphing Quadratic Functions in Standard Form y = ax 2 + bx + c

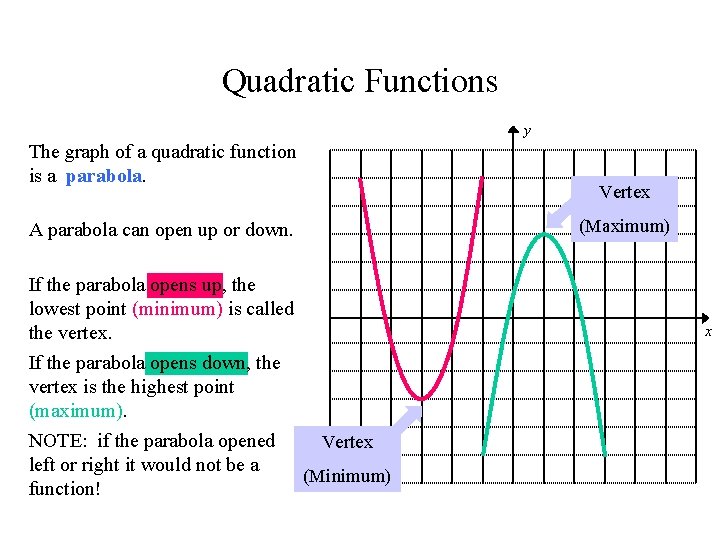
Quadratic Functions y The graph of a quadratic function is a parabola. Vertex (Maximum) A parabola can open up or down. If the parabola opens up, the lowest point (minimum) is called the vertex. x If the parabola opens down, the vertex is the highest point (maximum). NOTE: if the parabola opened left or right it would not be a function! Vertex (Minimum)

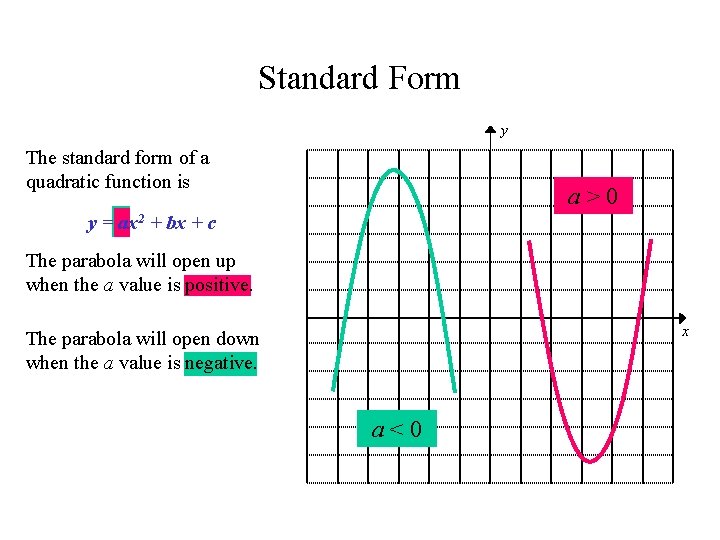
Standard Form y The standard form of a quadratic function is a>0 y = ax 2 + bx + c The parabola will open up when the a value is positive. x The parabola will open down when the a value is negative. a<0

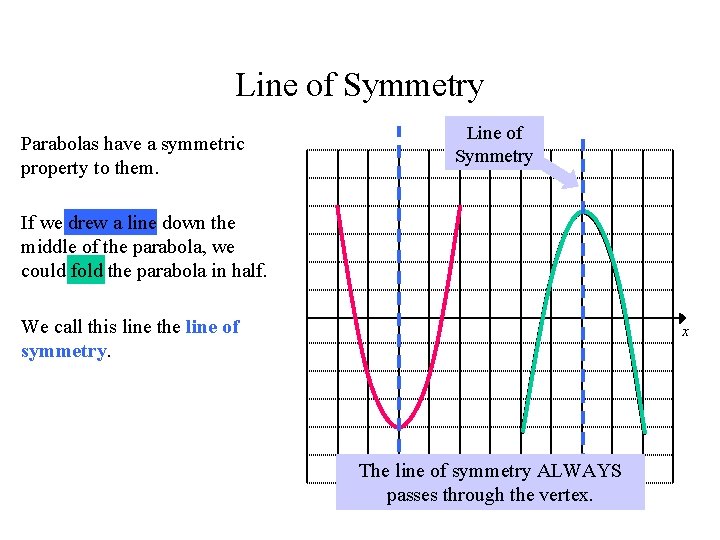
Line of Symmetry Parabolas have a symmetric property to them. Lineyof Symmetry If we drew a line down the middle of the parabola, we could fold the parabola in half. We call this line the line of symmetry. x The line of symmetry ALWAYS passes through the vertex.

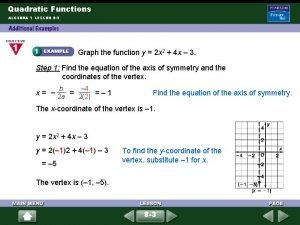
Finding the Line of Symmetry When a quadratic function is in standard form y = ax 2 + bx + c, The equation of the line of symmetry is This is best read as … the opposite of b divided by the quantity of 2 times a. For example… Find the line of symmetry of y = 3 x 2 – 18 x + 7

Finding the Vertex We know the line of symmetry always goes through the vertex. Thus, the line of symmetry gives us the x – coordinate of the vertex. To find the y – coordinate of the vertex, we need to plug the x – value into the original equation. For example, Find the vertex y = – 2 x 2 + 8 x – 3

A Quadratic Function in Standard Form The standard form of a quadratic function is given by y = ax 2 + bx + c STEP 1: Find the line of symmetry STEP 2: Find the vertex STEP 3: Make a table of values using x values close to the line of symmetry. (Put the vertex in the middle of your table of values. )

A Quadratic Function in Standard Form Example 1 y a. Graph b. Find and label the axis of symmetry. c. Find the maximum/minimum d. Find the domain & range y = 2 x 2 – 4 x – 1 x

A Quadratic Function in Standard Form Example 2 a. Graph b. Find and label the axis of symmetry. c. Find the maximum/minimum d. Find the domain & range y = x 2 - 2 x – 1 y x

A Quadratic Function in Standard Form Example 3 a. Graph b. Find and label the axis of symmetry. c. Find the maximum/minimum d. Find the domain & range y = -1/6 x 2 – x – 3 y x