Quadratic Functions Solving by Graphing Quadratic Function Standard

Quadratic Functions Solving by Graphing

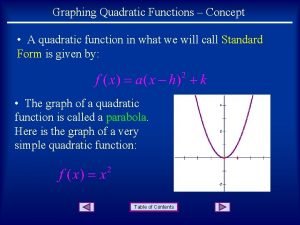
Quadratic Function Standard Form: f(x) = ax 2 + bx + c

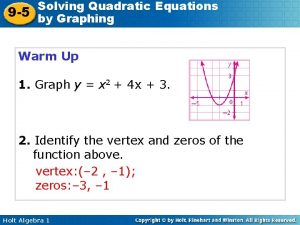
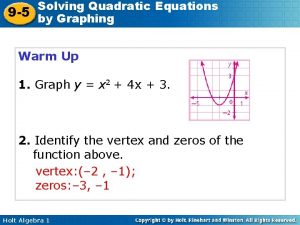
Solving Quadratic Equations To solve, we need to find the value of x when y = 0 or f(x) = 0. Located at: x-intercepts Referred to as: solutions, zeros, or roots.
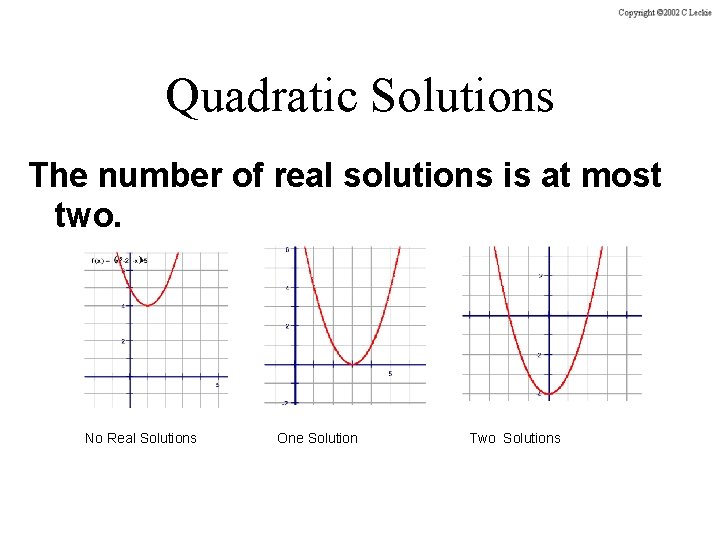
Quadratic Solutions The number of real solutions is at most two. No Real Solutions One Solution Two Solutions

Identifying Solutions 2 Example f(x) = x - 4 Solutions are x = -2 and x = 2.
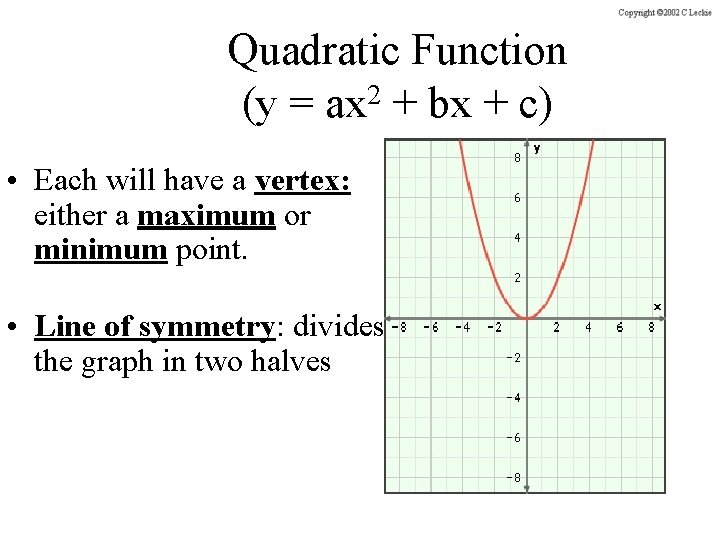
Quadratic Function 2 (y = ax + bx + c) • Each will have a vertex: either a maximum or minimum point. • Line of symmetry: divides the graph in two halves
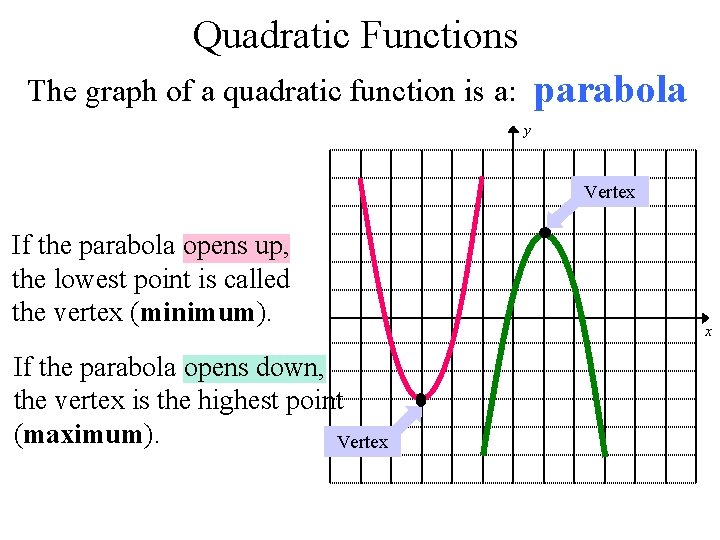
Quadratic Functions parabola The graph of a quadratic function is a: y Vertex If the parabola opens up, the lowest point is called the vertex (minimum). If the parabola opens down, the vertex is the highest point (maximum). Vertex x

Axis of Symmetry Parabolas are symmetric. Axis of symmetry Axisy of Symmetry x The Axis of symmetry ALWAYS passes through the vertex.
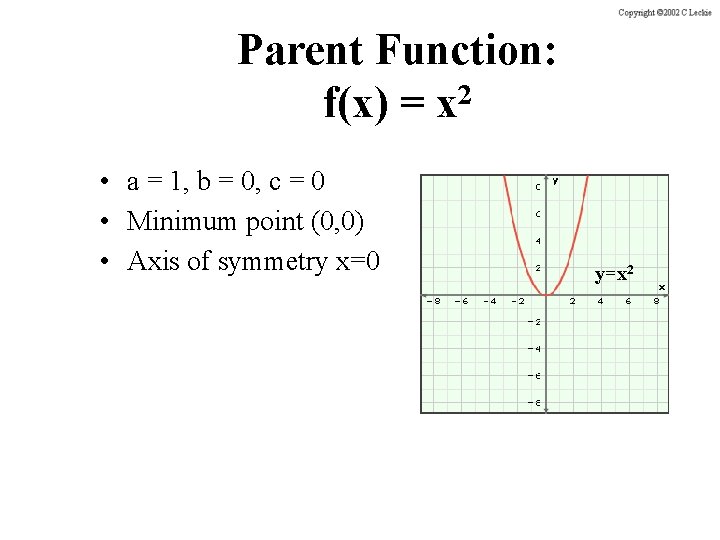
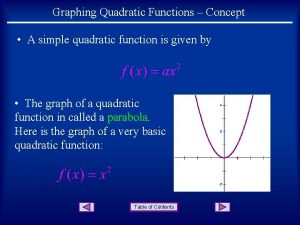
Parent Function: 2 f(x) = x • a = 1, b = 0, c = 0 • Minimum point (0, 0) • Axis of symmetry x=0 y=x 2
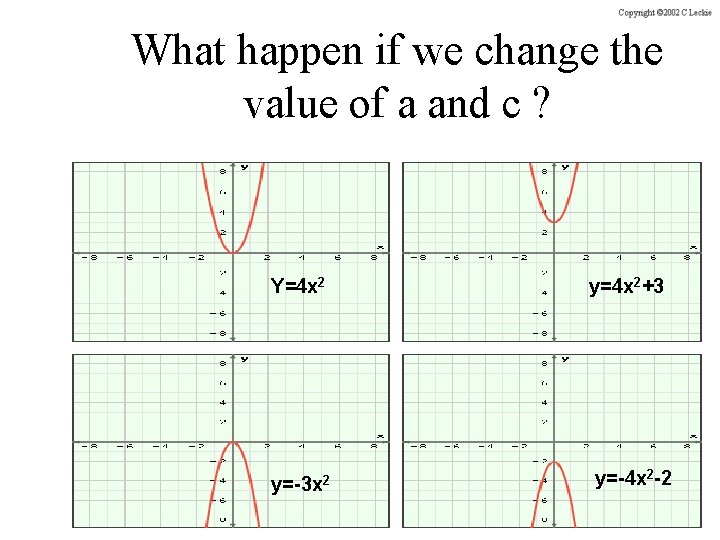
What happen if we change the value of a and c ? Y=4 x 2 y=4 x 2+3 y=-3 x 2 y=-4 x 2 -2

Conclusion (y = ax 2+bx+c) • When a is positive Concave (opens up) • When a is negative, Convex (opens down) • When c is positive, Moves Up • When c is negative, Moves Down
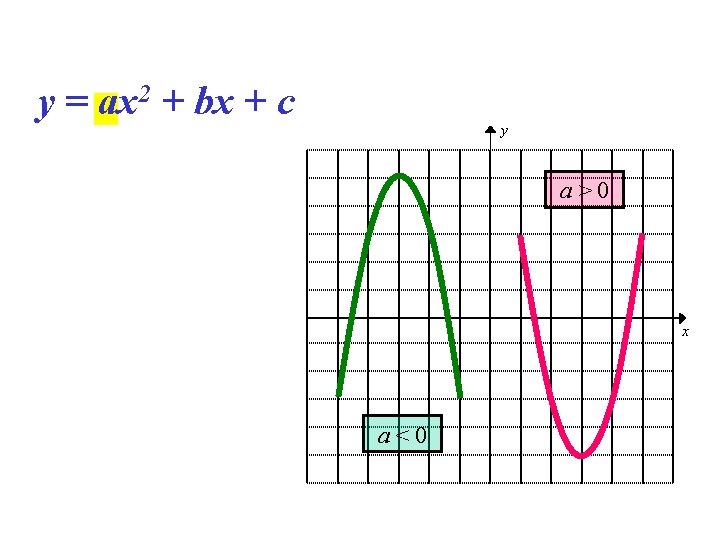
y = ax 2 + bx + c y a>0 x a<0

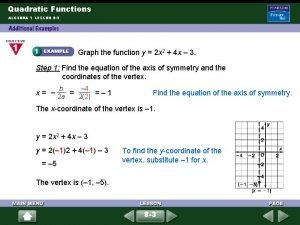
Finding the Axis of Symmetry When a quadratic function is in standard form y = ax 2 + bx + c, the equation of the Axis of symmetry is
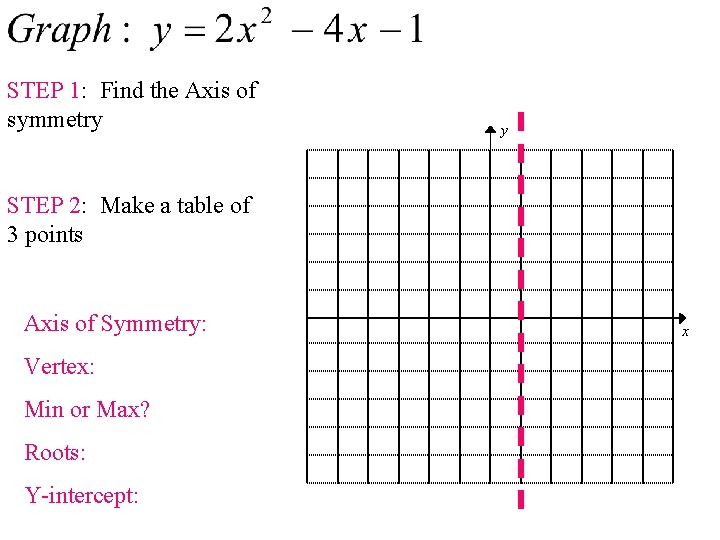
STEP 1: Find the Axis of symmetry y STEP 2: Make a table of 3 points Axis of Symmetry: Vertex: Min or Max? Roots: Y-intercept: x

y Axis of Symmetry: Vertex: Min or Max? Roots: Y-intercept: x
- Slides: 15