9 1 Graphing Quadratic Functions Quadratic Function in

n n Parabolas can open up or down. The point where the curve changes

Graph a quadratic function y = x 2 – x – 2 a >

Each parabola has an axis of symmetry This is where you could “fold” the

Slides: 6

Download presentation

9. 1 Graphing Quadratic Functions Quadratic Function: in the form of… n y = ax 2 + bx + c, where a = 0. n The graph of a quadratic function is a parabola (generally looks like a U). n

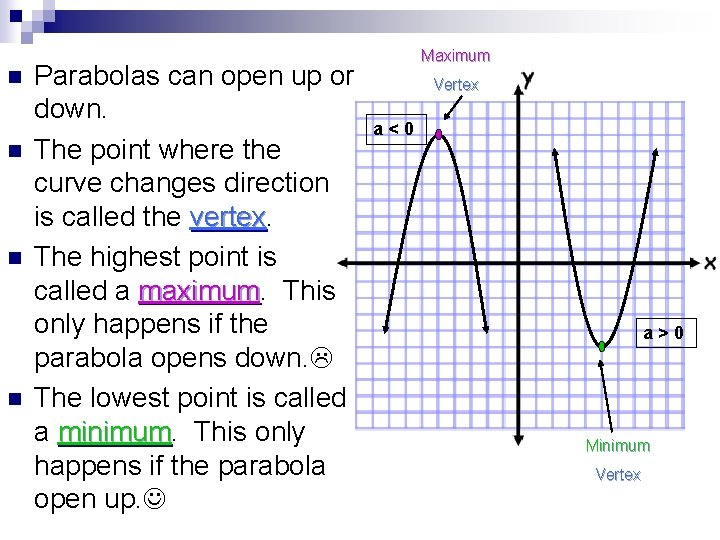
n n Parabolas can open up or down. The point where the curve changes direction is called the vertex The highest point is called a maximum This only happens if the parabola opens down. The lowest point is called a minimum This only happens if the parabola open up. Maximum Vertex a<0 a>0 Minimum Vertex

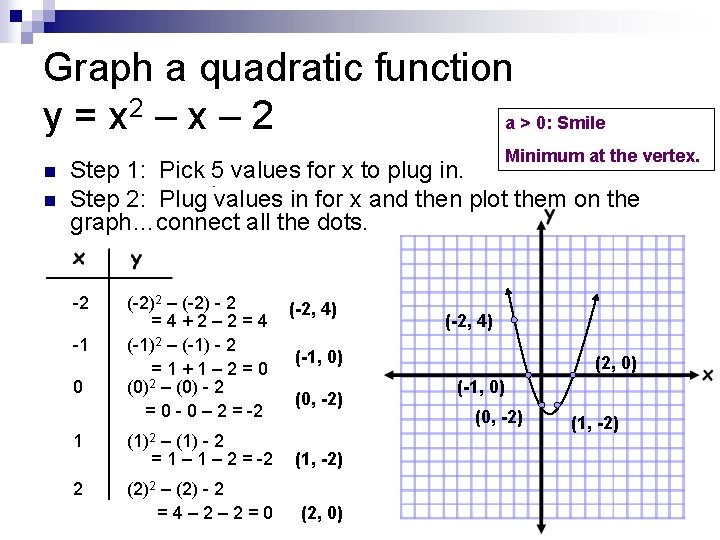
Graph a quadratic function y = x 2 – x – 2 a > 0: Smile n n Minimum at the vertex. Step 1: Pick 5 values for x to plug in. Step 2: Plug values in for x and then plot them on the graph…connect all the dots. -2 -1 0 (-2)2 – (-2) - 2 =4+2– 2=4 (-1)2 – (-1) - 2 =1+1– 2=0 2 (0) – (0) - 2 = 0 - 0 – 2 = -2 (-2, 4) (-1, 0) (0, -2) 1 (1)2 – (1) - 2 = 1 – 2 = -2 (1, -2) 2 (2)2 – (2) - 2 =4– 2– 2=0 (2, 0) (-1, 0) (0, -2) (1, -2)

Each parabola has an axis of symmetry This is where you could “fold” the parabola in half and the sides would match up (symmetrical). n The axis goes through the vertex. n The equation for finding the axis of symmetry is… given a n quadratic function

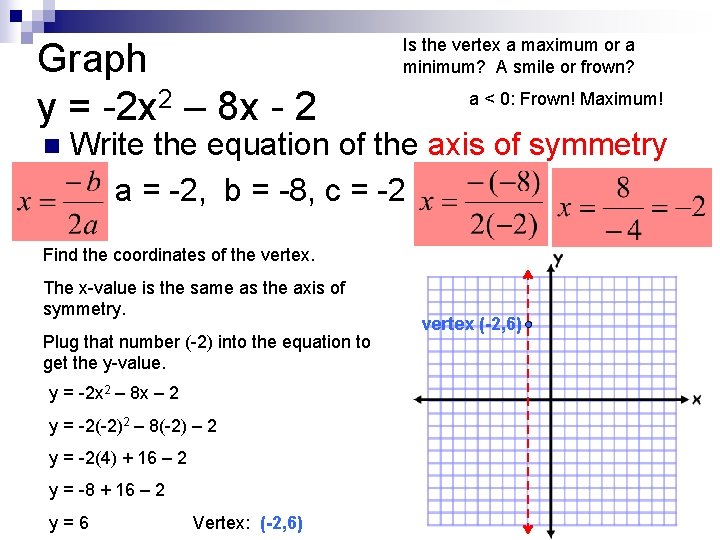
Graph y = -2 x 2 – 8 x - 2 n Is the vertex a maximum or a minimum? A smile or frown? a < 0: Frown! Maximum! Write the equation of the axis of symmetry a = -2, b = -8, c = -2 Find the coordinates of the vertex. The x-value is the same as the axis of symmetry. Plug that number (-2) into the equation to get the y-value. y = -2 x 2 – 8 x – 2 y = -2(-2)2 – 8(-2) – 2 y = -2(4) + 16 – 2 y = -8 + 16 – 2 y=6 Vertex: (-2, 6) vertex (-2, 6)

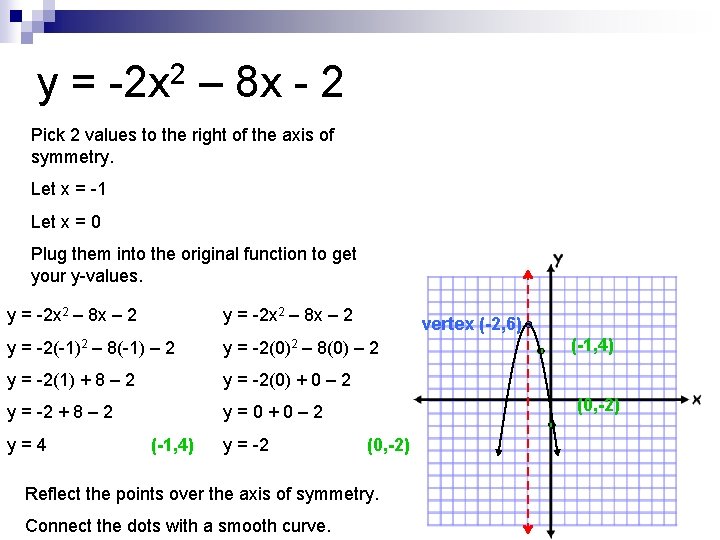
y = -2 x 2 – 8 x - 2 Pick 2 values to the right of the axis of symmetry. Let x = -1 Let x = 0 Plug them into the original function to get your y-values. y = -2 x 2 – 8 x – 2 y = -2(-1)2 – 8(-1) – 2 y = -2(0)2 – 8(0) – 2 y = -2(1) + 8 – 2 y = -2(0) + 0 – 2 y = -2 + 8 – 2 y=0+0– 2 y=4 (-1, 4) y = -2 vertex (-2, 6) (0, -2) Reflect the points over the axis of symmetry. Connect the dots with a smooth curve. (-1, 4)