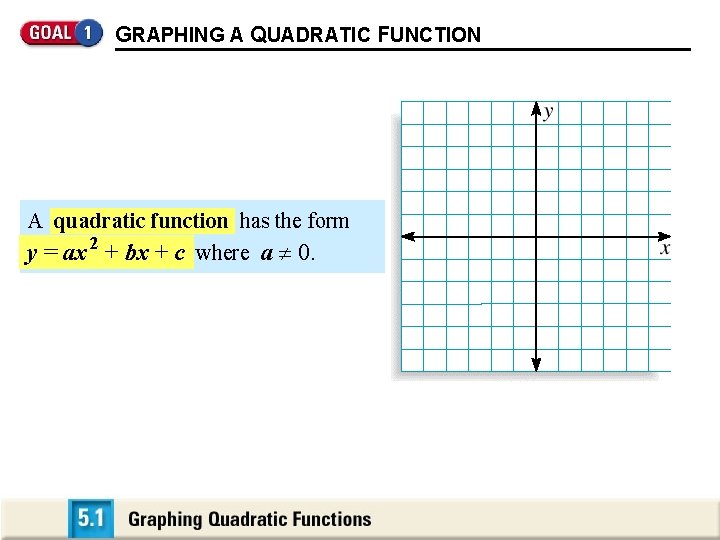
GRAPHING A QUADRATIC FUNCTION A quadratic function has

GRAPHING A QUADRATIC FUNCTION A quadratic function has the form y = ax 2 + bx + c where a 0.

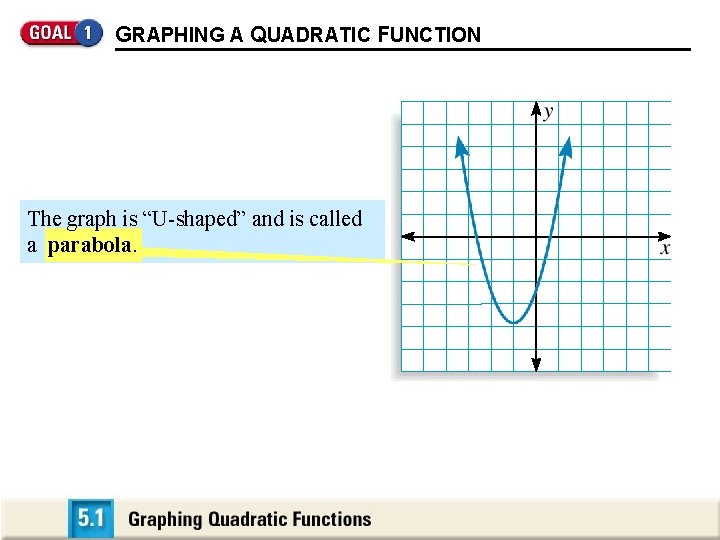
GRAPHING A QUADRATIC FUNCTION The graph is “U-shaped” and is called a parabola.

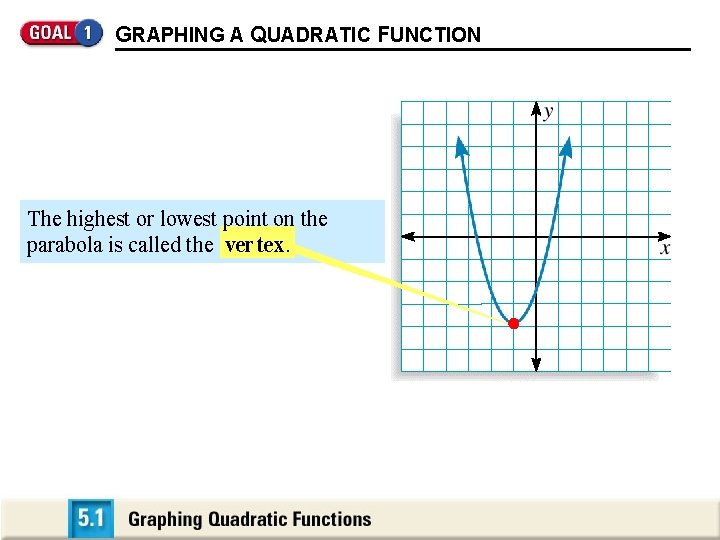
GRAPHING A QUADRATIC FUNCTION The highest or lowest point on the parabola is called the ver tex.

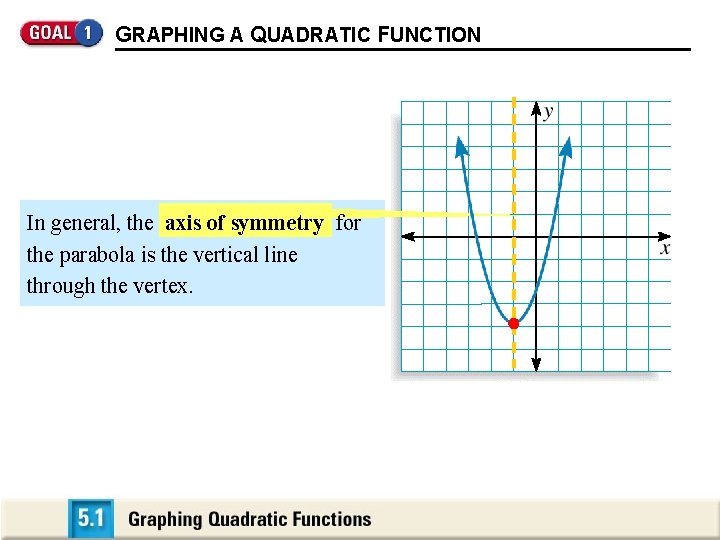
GRAPHING A QUADRATIC FUNCTION In general, the axis of symmetry for the parabola is the vertical line through the vertex.

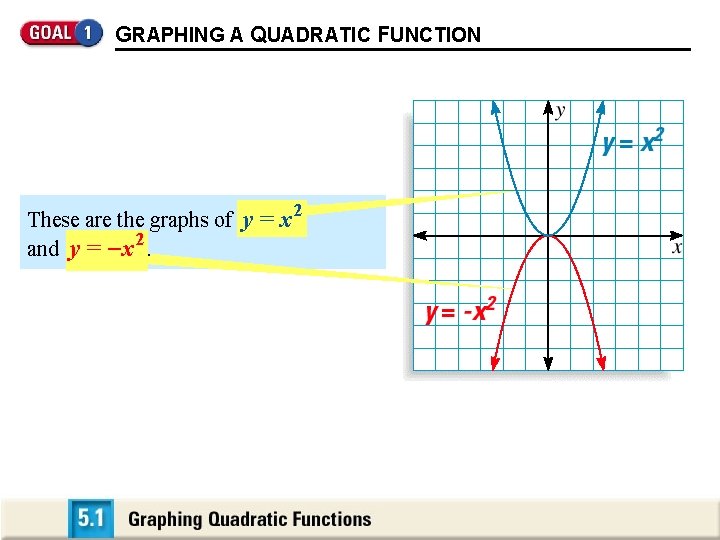
GRAPHING A QUADRATIC FUNCTION These are the graphs of y = x 2 and y = - x. 2

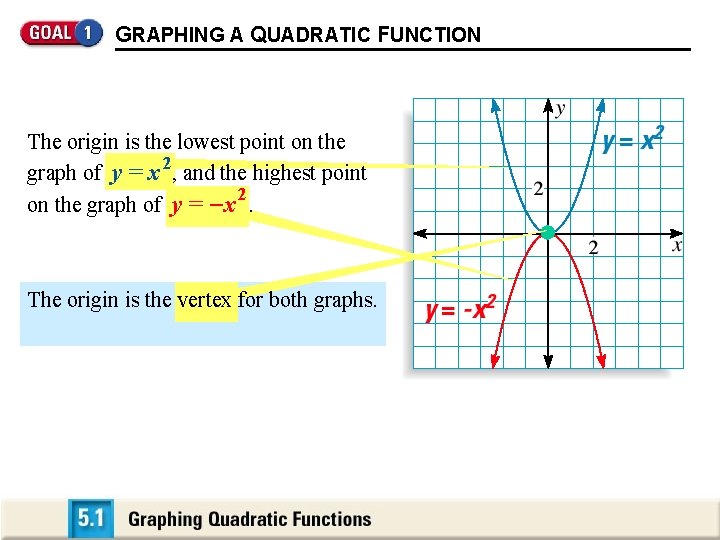
GRAPHING A QUADRATIC FUNCTION The origin is the lowest point on the 2 graph of y = x , and the highest point 2 on the graph of y = - x. The origin is the vertex for both graphs.

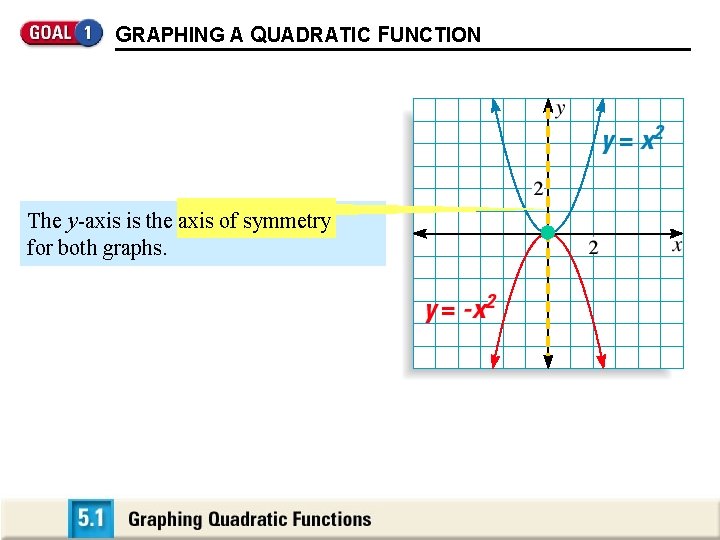
GRAPHING A QUADRATIC FUNCTION The y-axis is the axis of symmetry for both graphs.

GRAPHING A QUADRATIC FUNCTION CONCEPT THE GRAPH OF A QUADRATIC FUNCTION SUMMARY The graph of y = a x 2 + b x + c is a parabola with these characteristics: • The parabola opens up if a > 0 and opens down if a < 0. The parabola is wider than the graph of y = x 2 if a < 1 and narrower than the graph y = x 2 if a > 1. • The x-coordinate of the vertex is – b. 2 a b • The axis of symmetry is the vertical line x = – 2 a.

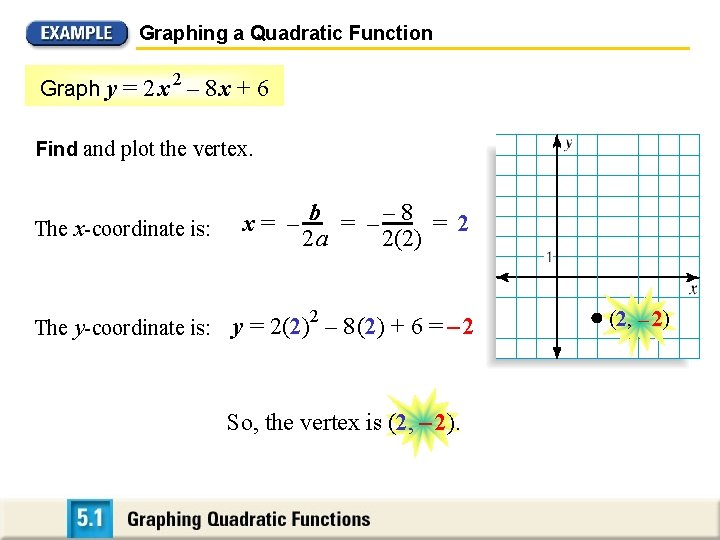
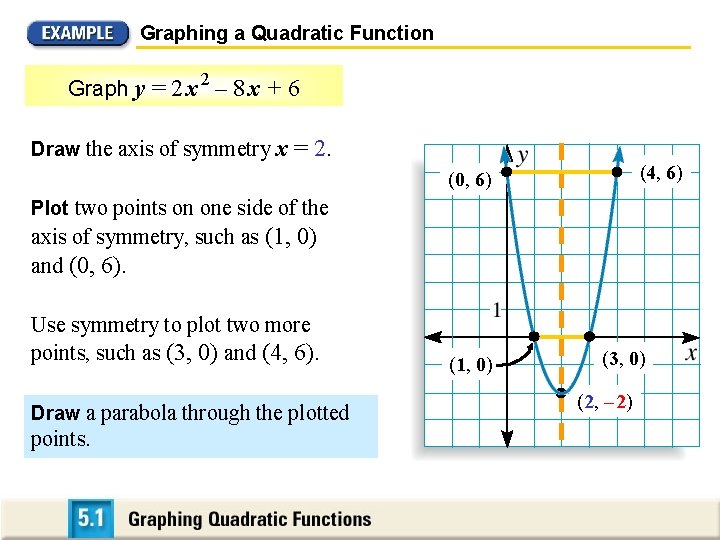
Graphing a Quadratic Function 2 Graph y = 2 x – 8 x + 6 SOLUTION Note that the coefficients for this function are a = 2, b = – 8, and c = 6. Since a > 0, the parabola opens up.

Graphing a Quadratic Function 2 Graph y = 2 x – 8 x + 6 Find and plot the vertex. The x-coordinate is: x = – b = –– 8 = 2 2(2) 2 a The y-coordinate is: y = 2(2)2 – 8 (2) + 6 = – 2 So, the vertex is (2, – 2)

Graphing a Quadratic Function 2 Graph y = 2 x – 8 x + 6 Draw the axis of symmetry x = 2. (4, 6) (0, 6) Plot two points on one side of the axis of symmetry, such as (1, 0) and (0, 6). Use symmetry to plot two more points, such as (3, 0) and (4, 6). Draw a parabola through the plotted points. (1, 0) (3, 0) (2, – 2)

GRAPHING A QUADRATIC FUNCTION VERTEX AND INTERCEPT FORMS OF A QUADRATIC FUNCTION FORM OF QUADRATIC FUNCTION CHARACTERISTICS OF GRAPH Vertex form: y = a (x – h)2 + k The vertex is (h, k ). The axis of symmetry is x = h. Intercept form: y = a (x – p )(x – q ) The x -intercepts are p and q. The axis of symmetry is halfway between ( p , 0 ) and (q , 0 ). For both forms, the graph opens up if a > 0 and opens down if a < 0.

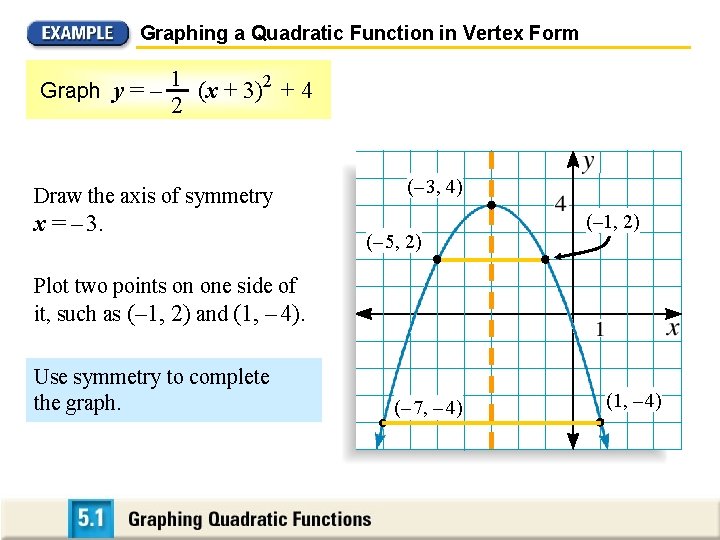
Graphing a Quadratic Function Graph y = – 1 2 (x + 3)2 + 4 SOLUTION (– 3, 4) The function is in vertex form y = a (x – h)2 + k. a = – 1 , h = – 3, and k = 4 2 a < 0, the parabola opens down. To graph the function, first plot the vertex (h, k) = (– 3, 4).

Graphing a Quadratic Function in Vertex Form Graph y = – 1 2 (x + 3)2 + 4 Draw the axis of symmetry x = – 3. (– 3, 4) (– 5, 2) (– 1, 2) Plot two points on one side of it, such as (– 1, 2) and (1, – 4). Use symmetry to complete the graph. (– 7, – 4) (1, – 4)

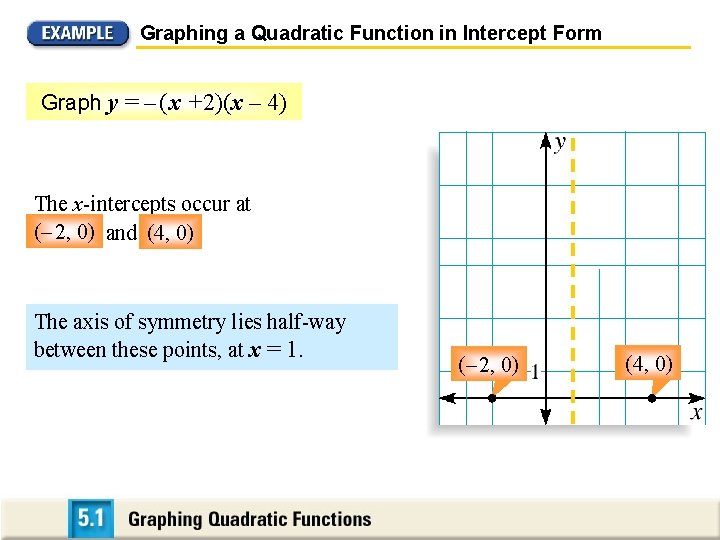
Graphing a Quadratic Function in Intercept Form Graph y = – ( x +2)(x – 4) SOLUTION The quadratic function is in intercept form y = a (x – p)(x – q), where a = – 1, p = – 2, and q = 4.

Graphing a Quadratic Function in Intercept Form Graph y = – ( x +2)(x – 4) The x-intercepts occur at (– 2, 2, 0) 0) and (4, 0). The axis of symmetry lies half-way between these points, at x = 1. (– 2, 0) (4, 0)

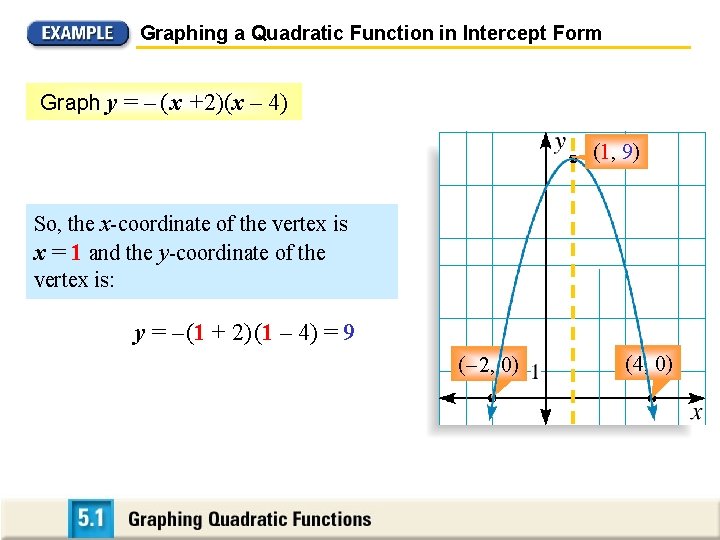
Graphing a Quadratic Function in Intercept Form Graph y = – ( x +2)(x – 4) (1, 9) So, the x-coordinate of the vertex is x = 1 and the y-coordinate of the vertex is: y = – (1 + 2) (1 – 4) = 9 (– 2, 0) (4, 0)

GRAPHING A QUADRATIC FUNCTION You can change quadratic functions from intercept form or vertex form to standard form by multiplying algebraic expressions. One method for multiplying expressions containing two terms is FOIL. Using this method, you add the products of the First terms, the O uter terms, the Inner terms, and the Last terms.

GRAPHING A QUADRATIC FUNCTION ( x + 3 )( x + 5 ) = x 2 + 5 x + 3 x + 15 = x 2 + 8 x + 15 F O I L Inner First Last Outer