Graphing Quadratic Functions Converting General Form To Standard









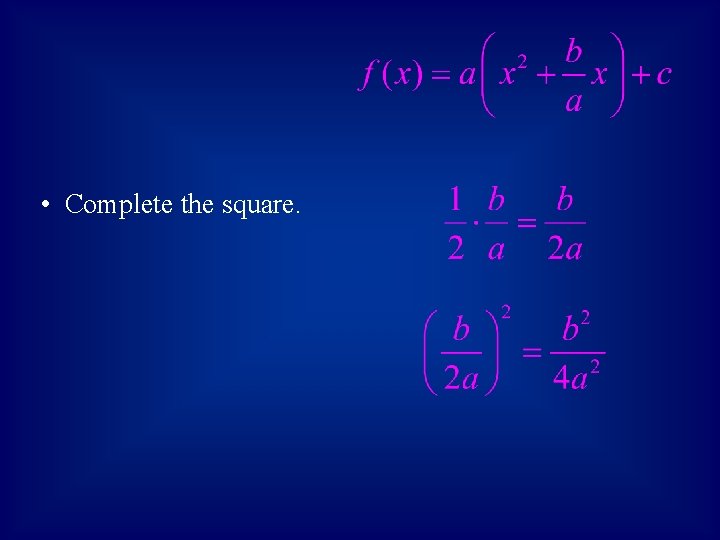







- Slides: 17

Graphing Quadratic Functions Converting General Form To Standard Form • The standard form and general form of quadratic functions are given below. Standard Form General Form

• It is assumed that you have already viewed the previous slide show titled Graphing Quadratic Functions – Standard Form • One way to graph the general form of a quadratic function is to manipulate it into the standard form, and then simply graph the standard form, as in the previous module. • The method used to do the conversion from general to standard form is completing the square. If you have forgotten how to complete the square, it is suggested that you re-visit a previous slide show titled Completing a Perfect Square Trinomial

• Example 1: Convert the function from general form to standard form. • Use the process of completing the square on the right hand side of the function. • Note - since this is not an equation, but a function, the process is slightly different than the completing the square method used to solve quadratic equations.

• Separate the quadratic and linear terms from the constant. • Factor out the leading coefficient.

• Complete the square. • The next step is where things are different from completing the square in equations.

• Add the 9 inside the parentheses. • Notice the coefficient out in front of the parentheses. We have actually added 3 times 9, or 27 to the right hand side of the function. • To balance this out, we must also subtract 27 from the right hand side.

• Factor the trinomial inside the parentheses, and simplify outside. • The original function that was in general form is now in standard form. This is the same function, but now in a different form.

• Example 2: Convert the function from general form to standard form. • Use the process of completing the square on the right hand side of the function.

• Separate the quadratic and linear terms from the constant. • Factor out the leading coefficient.
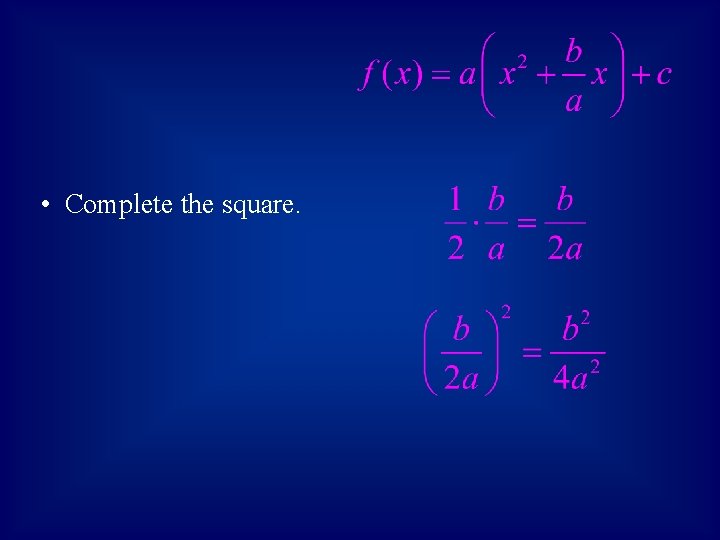
• Complete the square.

• Add the quantity inside the parenthesis • We have actually added a times the quantity to the right side of the function.

• The product is … • To balance out the function, subtract this last amount from the right side.

• Factor the trinomial inside the parentheses, and simplify outside.

• The original function that was in general form is now in standard form.

• An advantage of having the function in standard form is that the vertex is easily determined.

Important Fact • Given the general form of a quadratic function … …the x-value of the vertex is given by
