Graphing Quadratic Functions Standard Form It is assumed

  • Slides: 17
Download presentation
Graphing Quadratic Functions – Standard Form • It is assumed that you have already

Graphing Quadratic Functions – Standard Form • It is assumed that you have already viewed the previous slide show titled Graphing Quadratic Functions – Concept. • A quadratic function in what we will call Standard Form is given by: • The summary of the Concept slide show is given again on the next page.

SUMMARY Face Up Face Down Narrow Wide Vertex Axis of symmetry

SUMMARY Face Up Face Down Narrow Wide Vertex Axis of symmetry

• One more thing is needed before sketching the graph of a quadratic

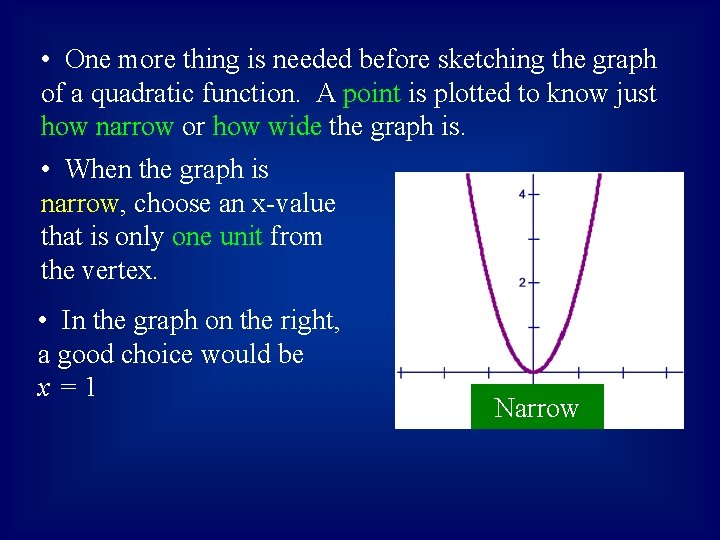
• One more thing is needed before sketching the graph of a quadratic function. A point is plotted to know just how narrow or how wide the graph is. • When the graph is narrow, choose an x-value that is only one unit from the vertex. • In the graph on the right, a good choice would be x=1 Narrow

• If the value x = 2 were chosen, then the corresponding y-value

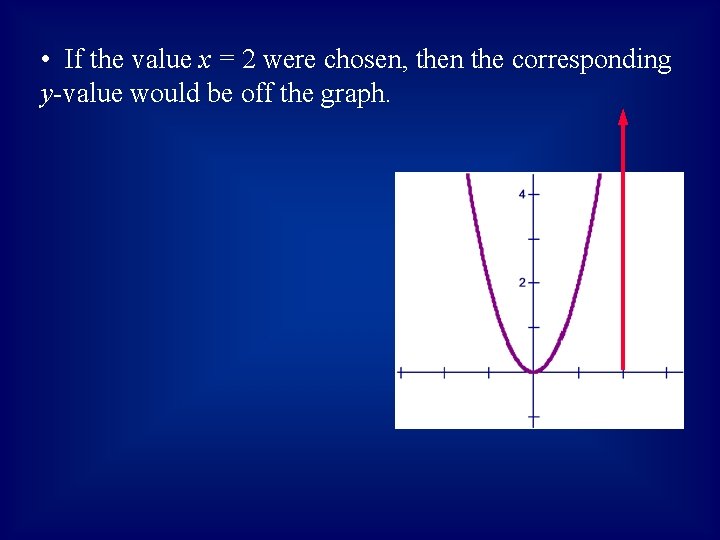
• If the value x = 2 were chosen, then the corresponding y-value would be off the graph.

• When the graph is wide, choose an x-value that is more than

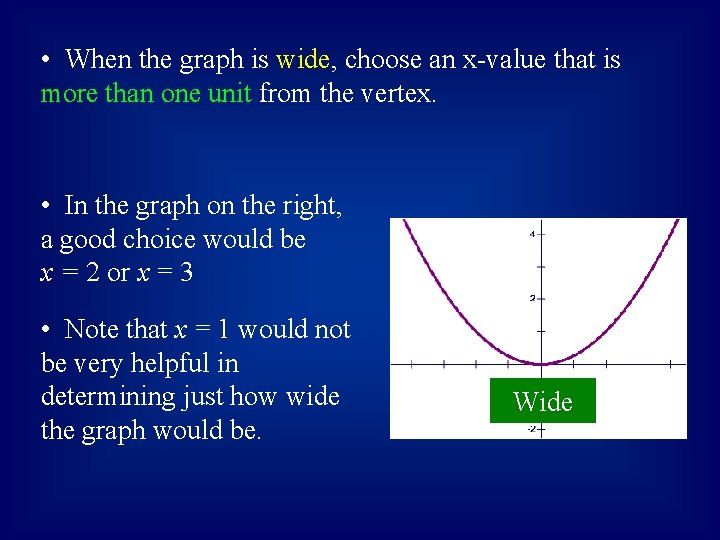
• When the graph is wide, choose an x-value that is more than one unit from the vertex. • In the graph on the right, a good choice would be x = 2 or x = 3 • Note that x = 1 would not be very helpful in determining just how wide the graph would be. Wide

SUMMARY Narrow Choose a value for x 1 unit away from the vertex. Wide

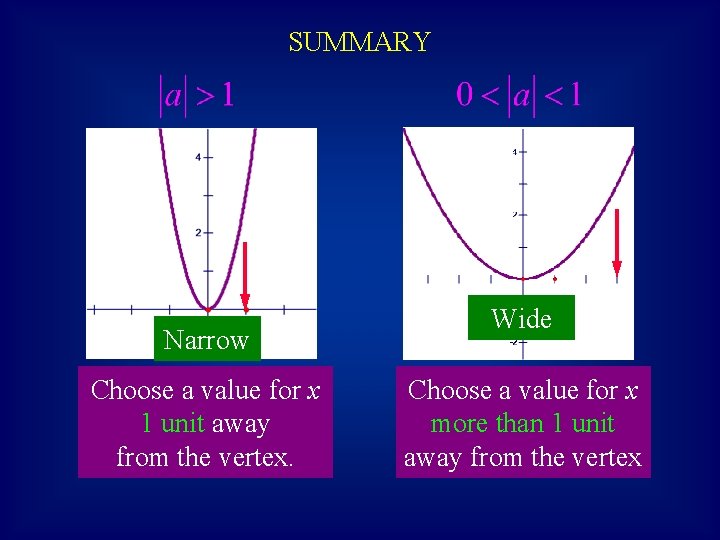
SUMMARY Narrow Choose a value for x 1 unit away from the vertex. Wide Choose a value for x more than 1 unit away from the vertex

• Example 1: Sketch the graph of the following function:

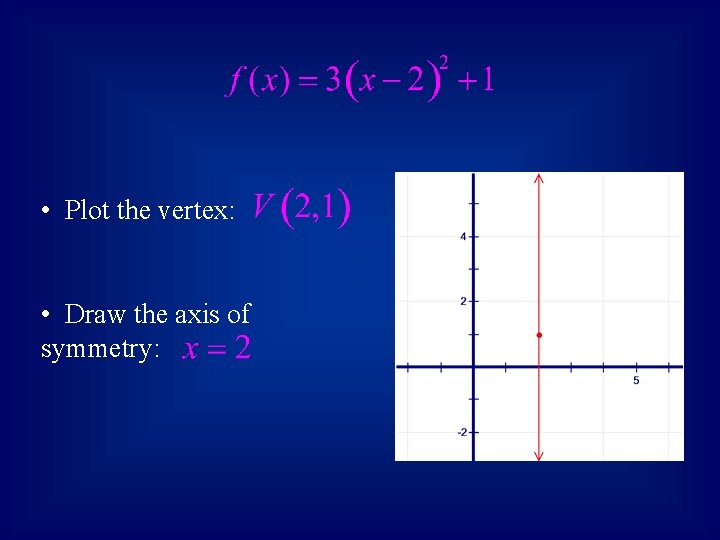
• Example 1: Sketch the graph of the following function:

• Plot the vertex: • Draw the axis of symmetry:

• Plot the vertex: • Draw the axis of symmetry:

• Since the graph is narrow, find a point that is only 1

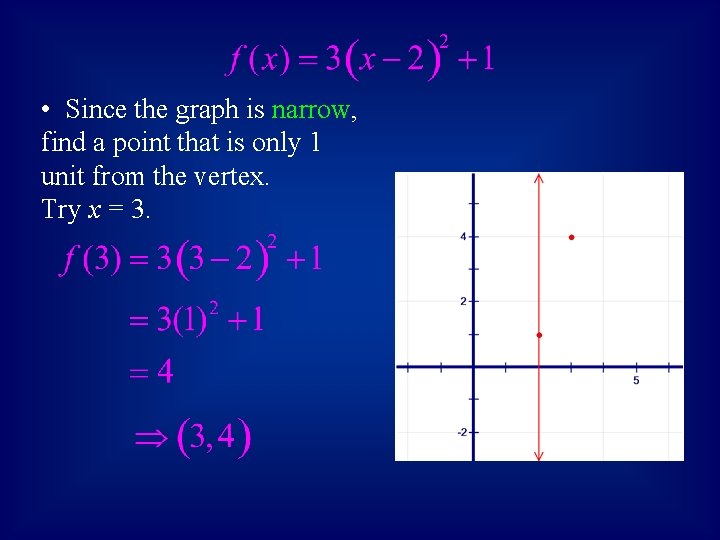
• Since the graph is narrow, find a point that is only 1 unit from the vertex. Try x = 3.

• Draw the right branch of the parabola using the vertex and the

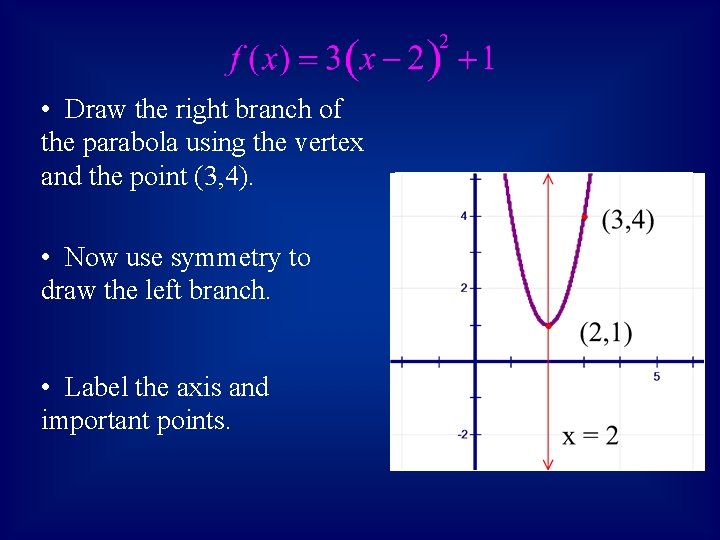
• Draw the right branch of the parabola using the vertex and the point (3, 4). • Now use symmetry to draw the left branch. • Label the axis and important points.

• Example 2: Sketch the graph of the following function: Face Down Vertex:

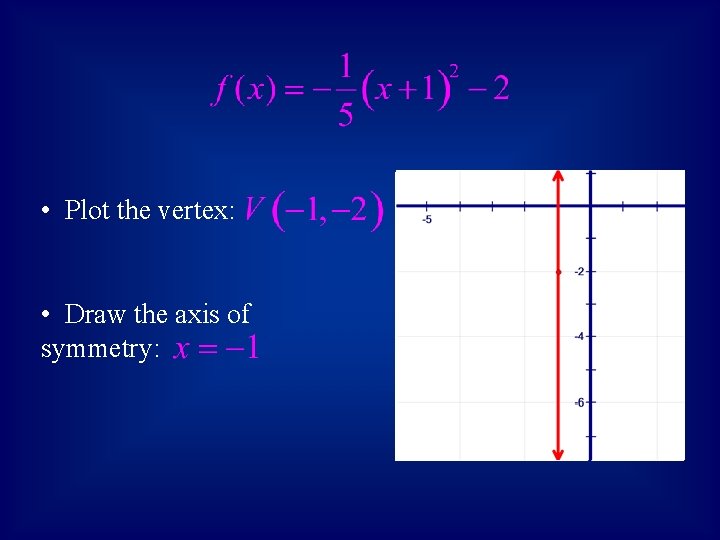
• Example 2: Sketch the graph of the following function: Face Down Vertex: Wide Axis:

• Plot the vertex: • Draw the axis of symmetry:

• Plot the vertex: • Draw the axis of symmetry:

• Since the graph is wide, find a point that is more than

• Since the graph is wide, find a point that is more than 1 unit from the vertex (-1, -2). • This problem presents another challenge, which is to avoid fractions if possible.

• Therefore, we want to meet two goals: 1. Select an x-value more

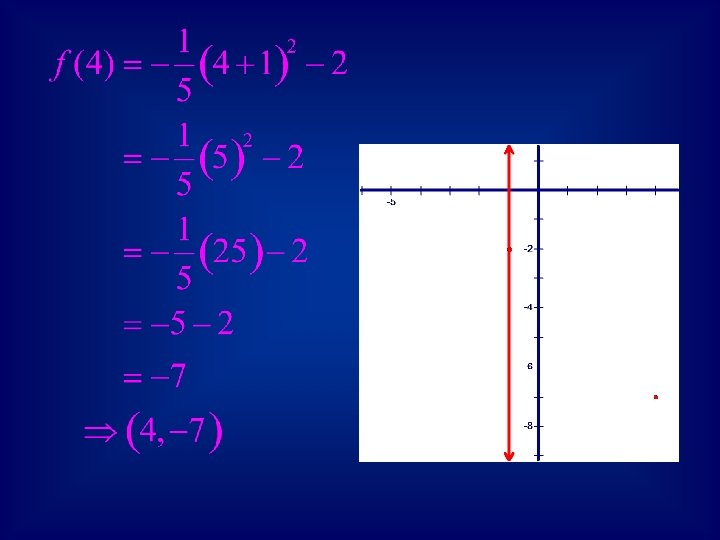
• Therefore, we want to meet two goals: 1. Select an x-value more than one unit to the right of the vertex (-1, -2). 2. Avoid fractions. • To meet goal #2, all that is needed is for the quantity that is squared to be divisible by 5. • An x-value of 4 meets this condition, and also satisfies goal #1.

• Draw the right branch of the parabola using the vertex and the

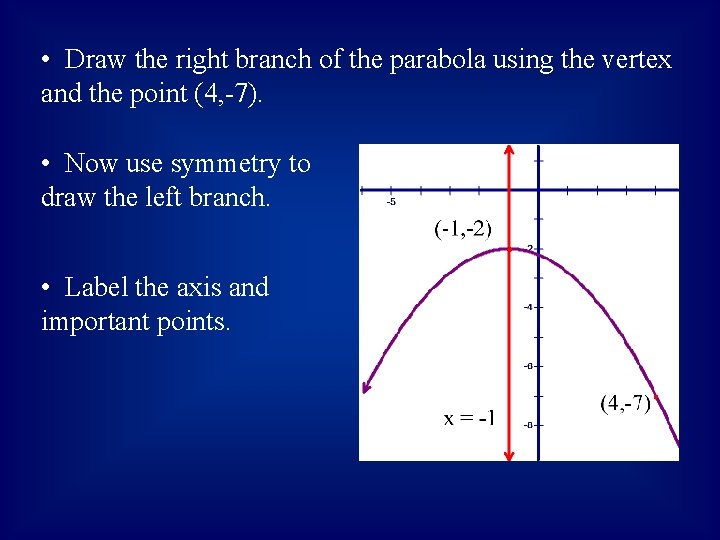
• Draw the right branch of the parabola using the vertex and the point (4, -7). • Now use symmetry to draw the left branch. • Label the axis and important points.