Solve Graph Sketch Find MaxMin Recall that quadratics





- Slides: 9


Solve Graph Sketch Find Max/Min

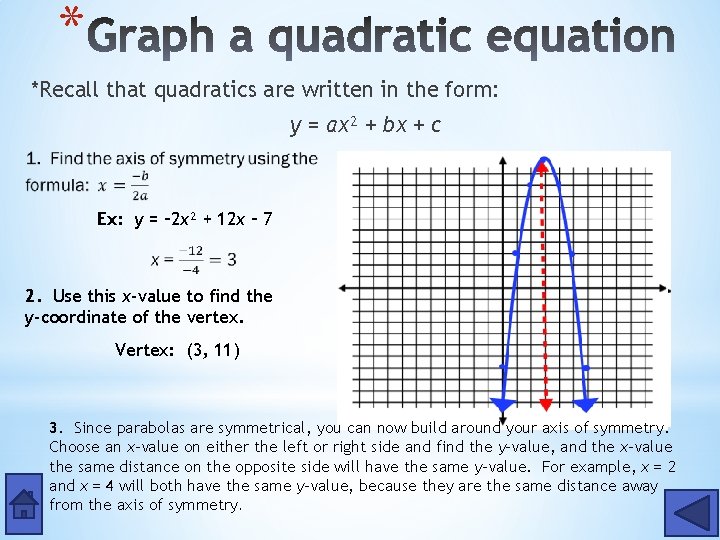
* *Recall that quadratics are written in the form: y = ax² + bx + c Ex: y = – 2 x² + 12 x – 7 2. Use this x-value to find the y-coordinate of the vertex. Vertex: (3, 11) 3. Since parabolas are symmetrical, you can now build around your axis of symmetry. Choose an x-value on either the left or right side and find the y-value, and the x-value the same distance on the opposite side will have the same y-value. For example, x = 2 and x = 4 will both have the same y-value, because they are the same distance away from the axis of symmetry.

* **RECALL** Quadratics are in the form: y = ax² + bx + c 2. Upward or downward? If a is positive, then the parabola will face upward If a is negative, then the parabola will face downward 3. Shift up or shift down? (*Only if b = 0) If c is positive, the vertex is c spaces up on the y-axis If c is negative, the vertex is c spaces down on the y-axis

* *Since the maximum or minimum value occurs at the vertex of the parabola, you need to find the coordinates of the vertex first. 2) Plug it back in to the quadratic equation to find the y-value of the vertex. 3) The maximum or minimum value is not the entire vertex. It is only the y-coordinate.

* Graphing Square Roots Quad. Formula

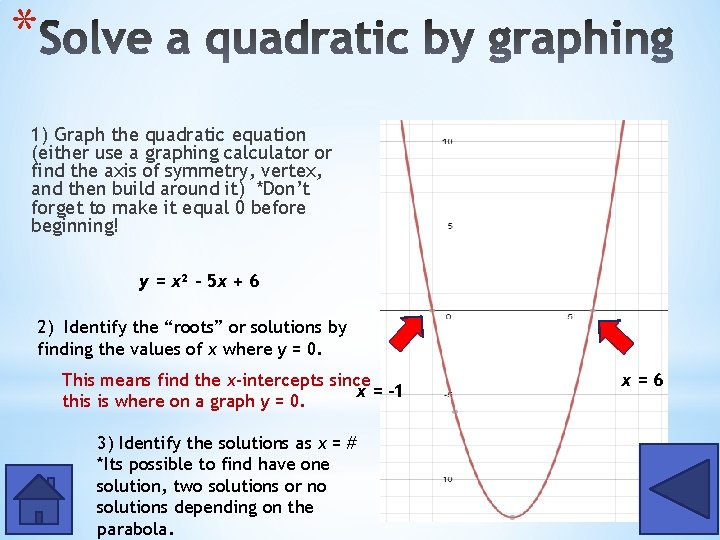
* 1) Graph the quadratic equation (either use a graphing calculator or find the axis of symmetry, vertex, and then build around it) *Don’t forget to make it equal 0 before beginning! y = x² - 5 x + 6 2) Identify the “roots” or solutions by finding the values of x where y = 0. This means find the x-intercepts since x = – 1 this is where on a graph y = 0. 3) Identify the solutions as x = # *Its possible to find have one solution, two solutions or no solutions depending on the parabola. x=6

* *If the quadratic is the form: y = ax² + c, then it can be solved by the square roots method. (*b = 0, if not, you can’t use square roots choose another method! 1) Isolate x² 2) · If x² > 0 · If x² < 0 · If x² = 0 Ex: 0 = 3 x² – 75 +75 75 = 3 x² 3 3 25 = x² There will be 2 answers. A positive and negative. There will be no solutions because you cannot take the square root of a negative number There will be one solution (which is 0)

* 1) Make sure the quadratic equation equals 0 and is in written in y = ax² + bx + c standard form. 2) 3) Identify a, b, and c. Plug into the formula and solve.