5 1 Graphing Quadratic Functions p 249 Definitions









- Slides: 17

5. 1 Graphing Quadratic Functions (p. 249) • Definitions • 3 forms for a quad. function • Steps for graphing each form • Examples • Changing between eqn. forms

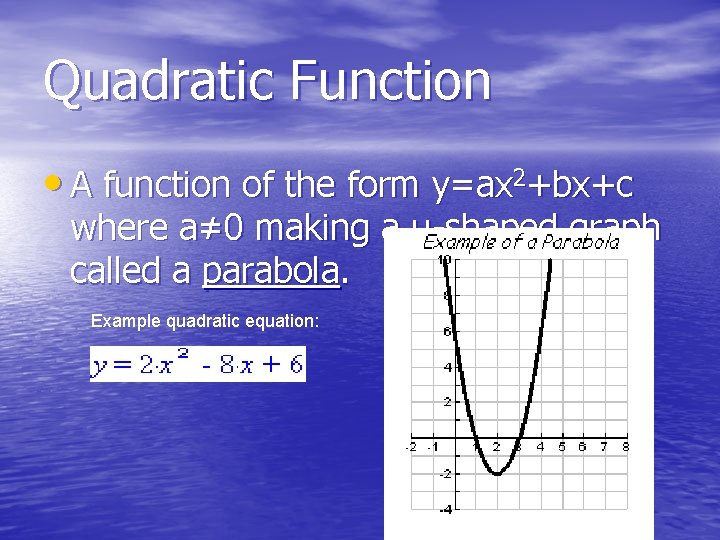
Quadratic Function • A function of the form y=ax 2+bx+c where a≠ 0 making a u-shaped graph called a parabola. Example quadratic equation:

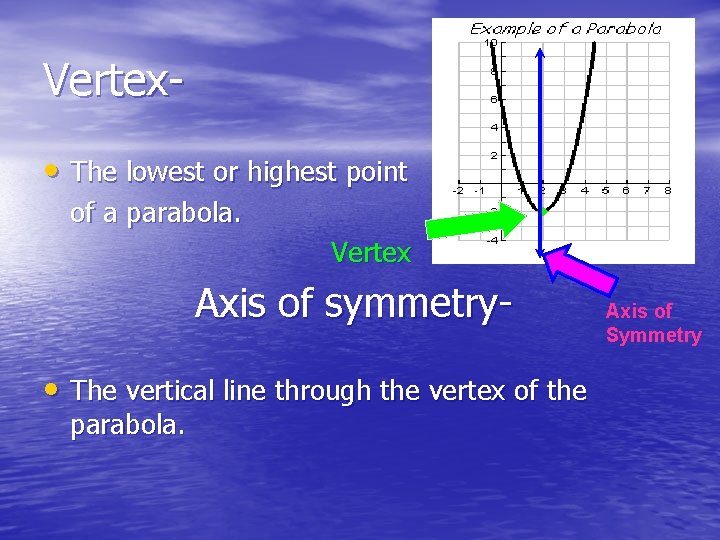
Vertex • The lowest or highest point of a parabola. Vertex Axis of symmetry • The vertical line through the vertex of the parabola. Axis of Symmetry

Standard Form Equation y=ax + bx + c 2 • If a is positive, u opens up • • • If a is negative, u opens down The x-coordinate of the vertex is at To find the y-coordinate of the vertex, plug the xcoordinate into the given eqn. The axis of symmetry is the vertical line x= Choose 2 x-values on either side of the vertex xcoordinate. Use the eqn to find the corresponding yvalues. Graph and label the 5 points and axis of symmetry on a coordinate plane. Connect the points with a smooth curve.

Vertex Form Equation y=a(x-h)2+k • If a is positive, parabola opens up If a is negative, parabola opens down. • The vertex is the point (h, k). • The axis of symmetry is the vertical line x=h. • Don’t forget about 2 points on either side of the vertex! (5 points total!)

Intercept Form Equation y=a(x-p)(x-q) • The x-intercepts are the points (p, 0) and (q, 0). • The axis of symmetry is the vertical line x= • The x-coordinate of the vertex is • To find the y-coordinate of the vertex, plug the x • -coord. into the equation and solve for y. If a is positive, parabola opens up If a is negative, parabola opens down.

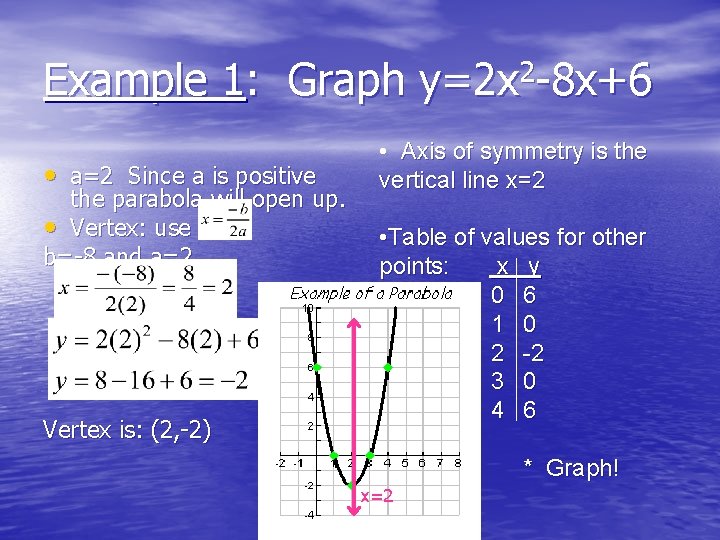
Example 1: Graph y=2 x 2 -8 x+6 • a=2 Since a is positive the parabola will open up. • Vertex: use b=-8 and a=2 Vertex is: (2, -2) • Axis of symmetry is the vertical line x=2 • Table of values for other points: x y 0 6 1 0 2 -2 3 0 4 6 * Graph! x=2

Now you try one! y=-x 2+x+12 * Open up or down? * Vertex? * Axis of symmetry? * Table of values with 5 points?


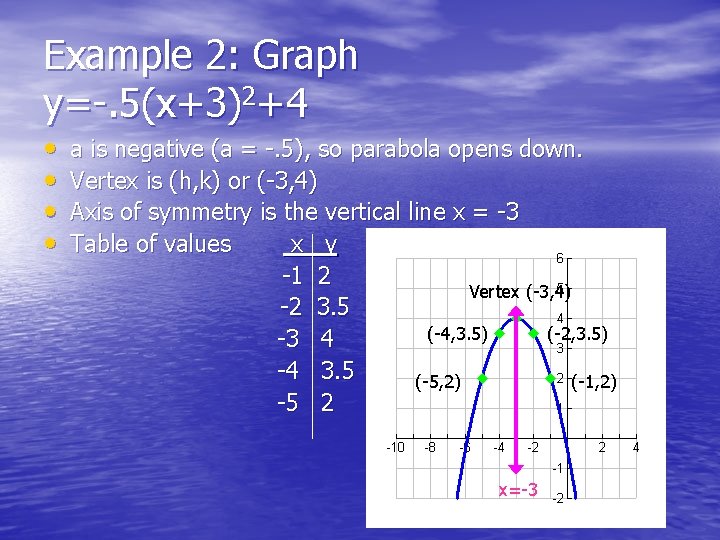
Example 2: Graph y=-. 5(x+3)2+4 • • a is negative (a = -. 5), so parabola opens down. Vertex is (h, k) or (-3, 4) Axis of symmetry is the vertical line x = -3 Table of values x y -1 2 Vertex (-3, 4) -2 3. 5 (-4, 3. 5) (-2, 3. 5) -3 4 -4 3. 5 (-5, 2) (-1, 2) -5 2 x=-3

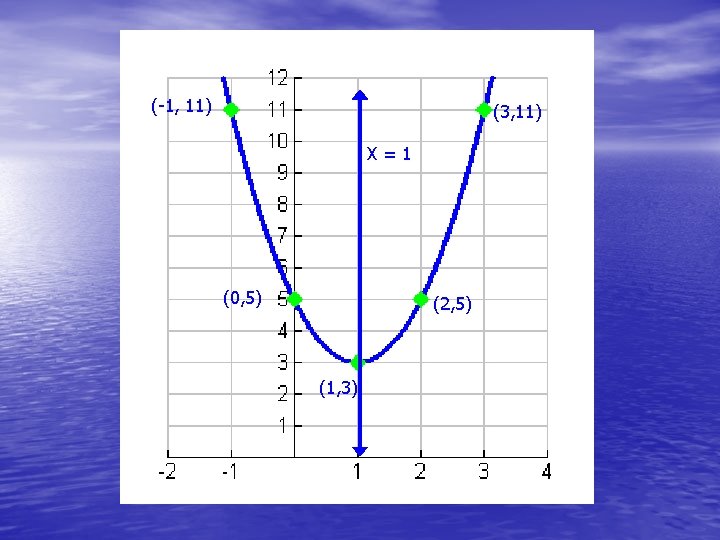
Now you try one! y=2(x-1)2+3 • Open up or down? • Vertex? • Axis of symmetry? • Table of values with 5 points?

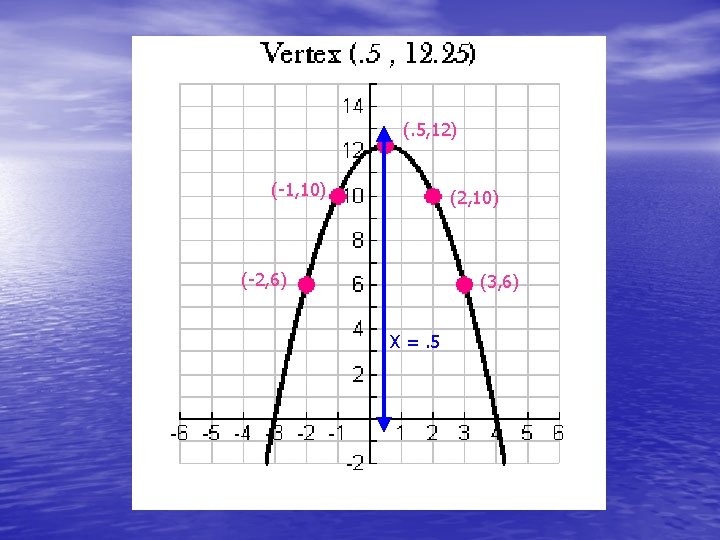
(-1, 11) (3, 11) X=1 (0, 5) (2, 5) (1, 3)

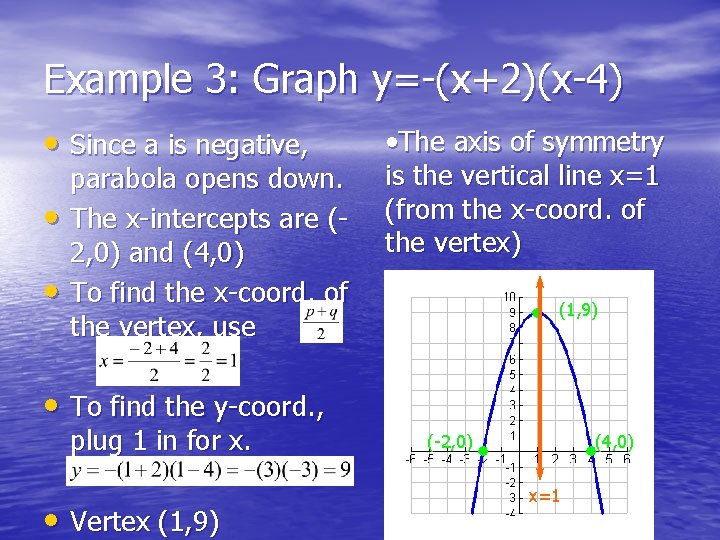
Example 3: Graph y=-(x+2)(x-4) • Since a is negative, • • parabola opens down. The x-intercepts are (2, 0) and (4, 0) To find the x-coord. of the vertex, use • The axis of symmetry is the vertical line x=1 (from the x-coord. of the vertex) (1, 9) • To find the y-coord. , plug 1 in for x. • Vertex (1, 9) (-2, 0) (4, 0) x=1

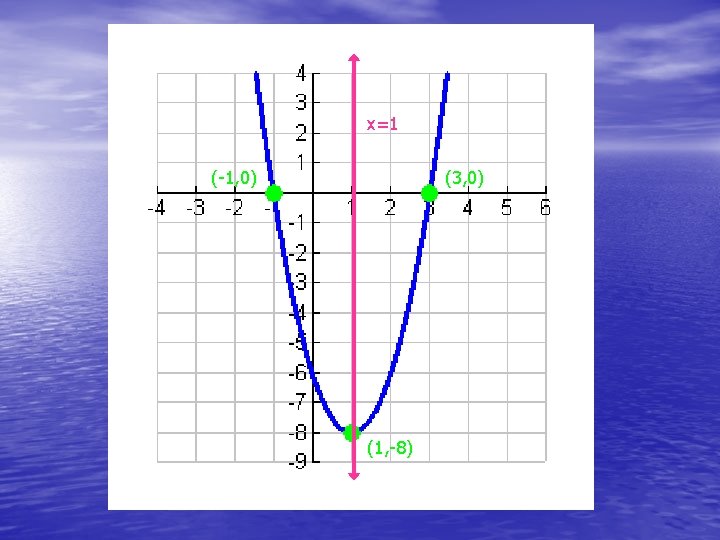
Now you try one! y=2(x-3)(x+1) • Open up or down? • X-intercepts? • Vertex? • Axis of symmetry?


Changing from vertex or intercepts form to standard form • The key is to FOIL! (first, outside, inside, last) • Ex: y=-(x+4)(x-9) Ex: y=3(x-1)2+8 =-(x 2 -9 x+4 x-36) =3(x-1)+8 =-(x 2 -5 x-36) =3(x 2 -x-x+1)+8 y=-x 2+5 x+36 =3(x 2 -2 x+1)+8 =3 x 2 -6 x+3+8 y=3 x 2 -6 x+11

Assignment