Functions 8 2 Characteristicsofof Quadratic Functions 8 2















- Slides: 21

Functions 8 -2 Characteristicsofof. Quadratic Functions 8 -2 Characteristics Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 1 Algebra 11 Holt Mc. Dougal

8 -2 Characteristics of Quadratic Functions Warm Up Find the x-intercept of each linear function. 1. y = 2 x – 3 2. Evaluate each quadratic function for the given input values. 3. y = – 3 x 2 + x – 2, when x = 2 Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions ESSENTIAL QUESTIONS 1. How do you find the zeros of a quadratic function from its graph? 2. How do you find the axis of symmetry and the vertex of a parabola? Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Vocabulary zero of a function axis of symmetry Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Recall that an x-intercept of a function is a value of x when y = 0. A zero of a function is an xvalue that makes the function equal to 0. Holt Mc. Dougal Algebra 1

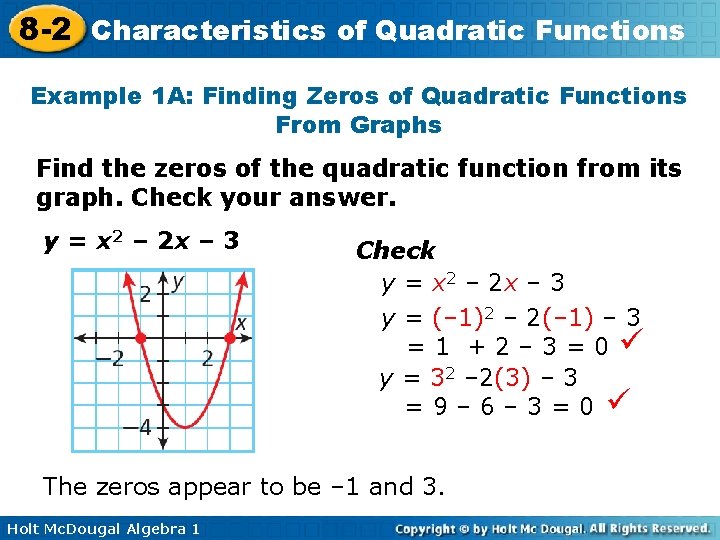
8 -2 Characteristics of Quadratic Functions Example 1 A: Finding Zeros of Quadratic Functions From Graphs Find the zeros of the quadratic function from its graph. Check your answer. y = x 2 – 2 x – 3 Check y = x 2 – 2 x – 3 y = (– 1)2 – 2(– 1) – 3 =1 +2– 3=0 y = 32 – 2(3) – 3 =9– 6– 3=0 The zeros appear to be – 1 and 3. Holt Mc. Dougal Algebra 1

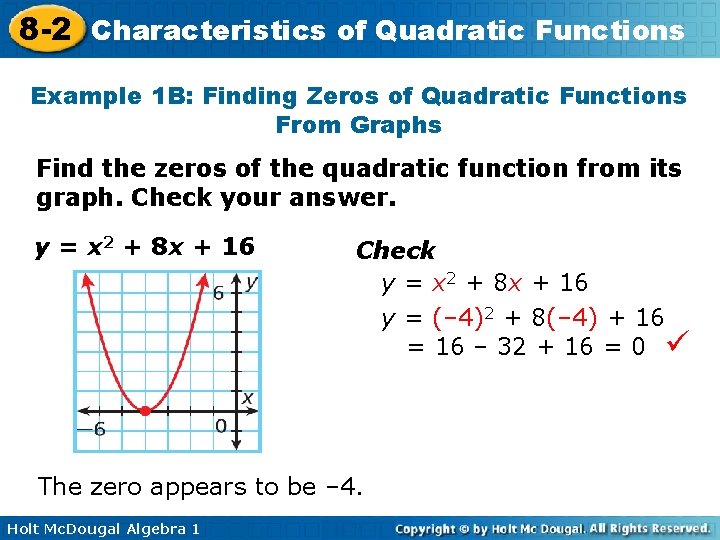
8 -2 Characteristics of Quadratic Functions Example 1 B: Finding Zeros of Quadratic Functions From Graphs Find the zeros of the quadratic function from its graph. Check your answer. y = x 2 + 8 x + 16 Check y = x 2 + 8 x + 16 y = (– 4)2 + 8(– 4) + 16 = 16 – 32 + 16 = 0 The zero appears to be – 4. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Helpful Hint Notice that if a parabola has only one zero, the zero is the x-coordinate of the vertex. Holt Mc. Dougal Algebra 1

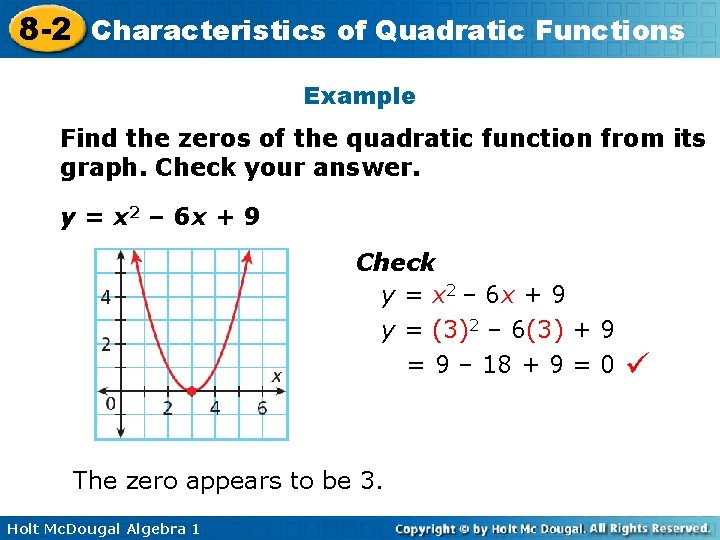
8 -2 Characteristics of Quadratic Functions Example Find the zeros of the quadratic function from its graph. Check your answer. y = x 2 – 6 x + 9 Check y = x 2 – 6 x + 9 y = (3)2 – 6(3) + 9 = 9 – 18 + 9 = 0 The zero appears to be 3. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Example Find the zeros of the quadratic function from its graph. Check your answer. y = – 2 x 2 – 2 The graph does not cross the x-axis, so there are no zeros of this function. Holt Mc. Dougal Algebra 1

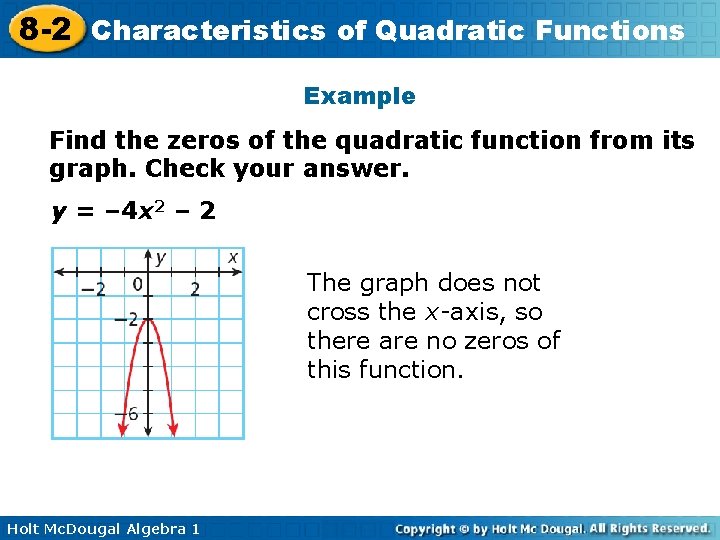
8 -2 Characteristics of Quadratic Functions Example Find the zeros of the quadratic function from its graph. Check your answer. y = – 4 x 2 – 2 The graph does not cross the x-axis, so there are no zeros of this function. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions A vertical line that divides a parabola into two symmetrical halves is the axis of symmetry. The axis of symmetry always passes through the vertex of the parabola. You can use the zeros to find the axis of symmetry. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Holt Mc. Dougal Algebra 1

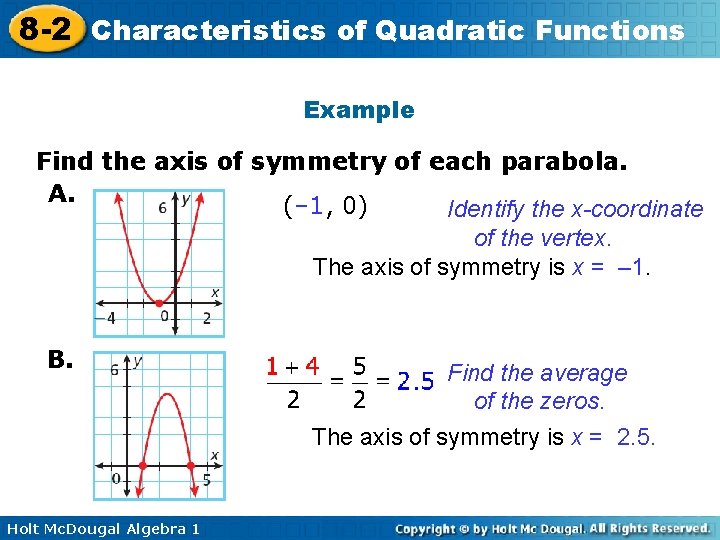
8 -2 Characteristics of Quadratic Functions Example Find the axis of symmetry of each parabola. A. (– 1, 0) Identify the x-coordinate of the vertex. The axis of symmetry is x = – 1. B. Holt Mc. Dougal Algebra 1 Find the average of the zeros. The axis of symmetry is x = 2. 5.

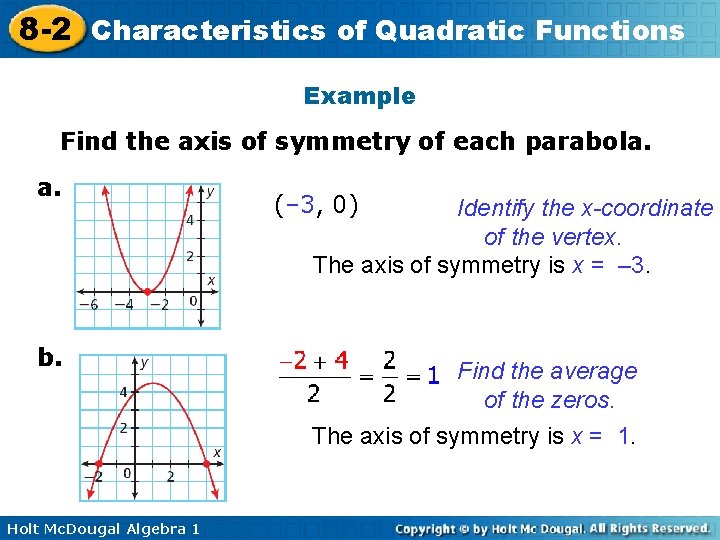
8 -2 Characteristics of Quadratic Functions Example Find the axis of symmetry of each parabola. a. b. Holt Mc. Dougal Algebra 1 (– 3, 0) Identify the x-coordinate of the vertex. The axis of symmetry is x = – 3. Find the average of the zeros. The axis of symmetry is x = 1.

8 -2 Characteristics of Quadratic Functions If a function has no zeros or they are difficult to identify from a graph, you can use a formula to find the axis of symmetry. The formula works for all quadratic functions. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Example: Finding the Axis of Symmetry by Using the Formula Find the axis of symmetry of the graph of y = – 3 x 2 + 10 x + 9. Step 1. Find the values of a and b. y = – 3 x 2 + 10 x + 9 a = – 3, b = 10 The axis of symmetry is Holt Mc. Dougal Algebra 1 Step 2. Use the formula.

8 -2 Characteristics of Quadratic Functions Example Find the axis of symmetry of the graph of y = 2 x 2 + x + 3. Step 1. Find the values of a and b. y = 2 x 2 + 1 x + 3 a = 2, b = 1 The axis of symmetry is Holt Mc. Dougal Algebra 1 Step 2. Use the formula. .

8 -2 Characteristics of Quadratic Functions Example: Finding the Vertex of a Parabola Find the vertex. y = – 3 x 2 + 6 x – 7 Step 1 Find the x-coordinate of the vertex. a = – 3, b = 6 Identify a and b. Substitute – 3 for a and 6 for b. The x-coordinate of the vertex is 1. Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Example: Continued Find the vertex. y = – 3 x 2 + 6 x – 7 Step 2 Find the corresponding y-coordinate. y = – 3 x 2 + 6 x – 7 = – 3(1)2 + 6(1) – 7 Use the function rule. Substitute 1 for x. = – 3 + 6 – 7 = – 4 Step 3 Write the ordered pair. The vertex is (1, – 4). Holt Mc. Dougal Algebra 1

8 -2 Characteristics of Quadratic Functions Lesson Quiz: Part I 1. Find the zeros and the axis of symmetry of the parabola. zeros: ( , ); x = ___ (axis of symmetry) 2. Find the axis of symmetry and the vertex of the graph of y = 3 x 2 + 12 x + 8. Vertex ( , ) , Holt Mc. Dougal Algebra 1 x = __ (axis of symmetry)