Review 8 5 Exponential Functions Quadratic Functions Linear

Review 8. 5 Exponential Functions Quadratic Functions Linear Functions

Identifying from an equation: Linear Quadratic Exponential Has an x with no exponent. Has an x 2 in the equation. Has an x as the exponent. y = 5 x + 1 y = ½x 2 x + 3 y = 6 y = 2 x 2 + 3 x – 5 y = x 2 + 9 x 2 + 4 y = 7 y = 3 x + 1 y = 52 x 4 x + y = 13

Examples: • LINEAR, QUADRATIC or EXPONENTIAL? a)y = 6 x + 3 b)y = 7 x 2 +5 x – 2 c)9 x + 3 = y d)42 x = 8

Examples: • LINEAR, QUADRATIC or EXPONENTIAL? a)y = 6 x + 3 EXPONENTIAL b)y = 7 x 2 +5 x – 2 QUADRATIC c)9 x + 3 = y LINEAR d)42 x = 8 EXPONENTIAL

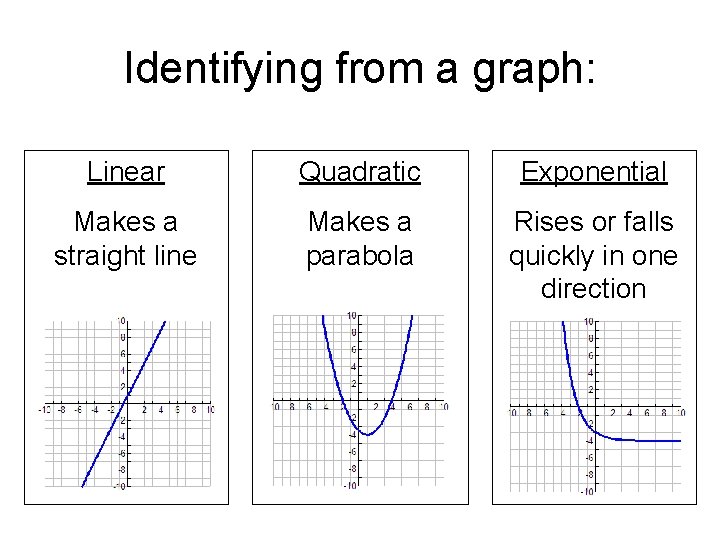
Identifying from a graph: Linear Quadratic Exponential Makes a straight line Makes a parabola Rises or falls quickly in one direction

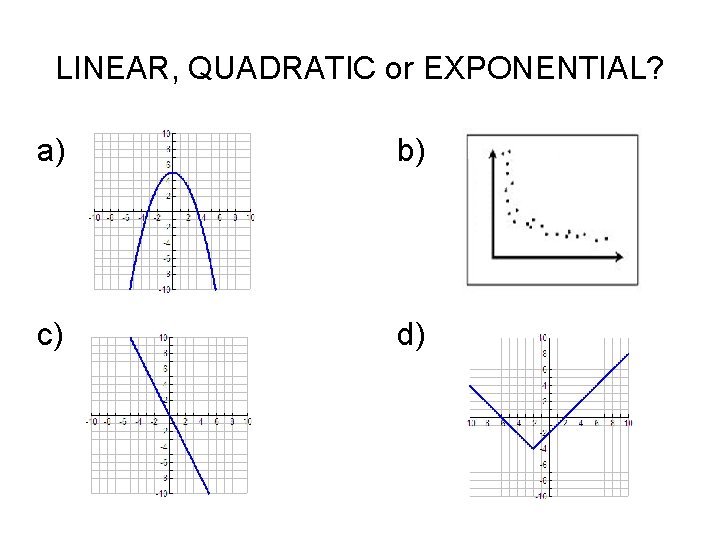
LINEAR, QUADRATIC or EXPONENTIAL? a) b) c) d)

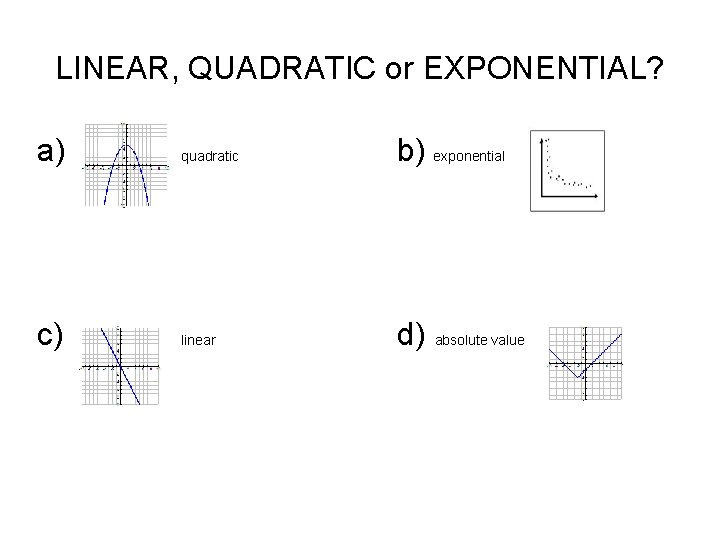
LINEAR, QUADRATIC or EXPONENTIAL? a) quadratic b) exponential c) linear d) absolute value

absolute value • Think of the definition of absolute value. It is a piecewise defined function. |x| = x, if x>=0 and -x if x<0. In other words, the graph of y=|x| is formed by two pieces of two lines. For the part of the domain where x-values are less than zero, the graph corresponds to the graph of y=-x. For parts of the domain where x-values are greater than or equal to zero, the graph corresponds to the graph of y=x. While the absolute value function does not satisfy the definition for a linear function, it is actually "parts" of two linear functions.

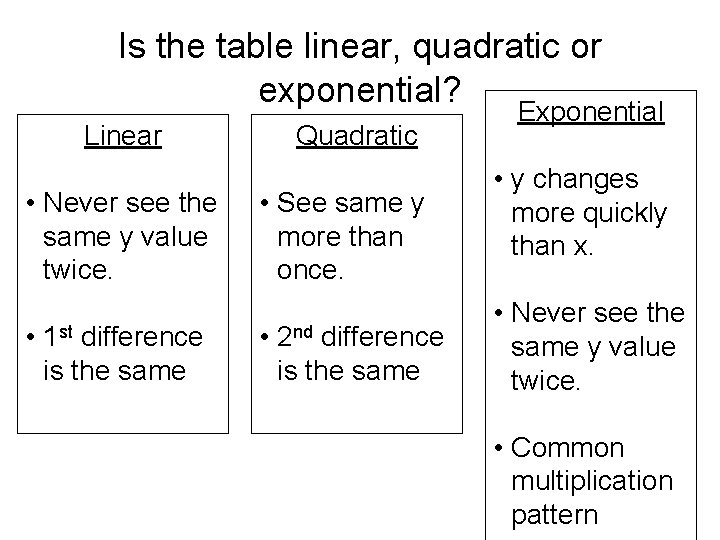
Is the table linear, quadratic or exponential? Linear • Never see the same y value twice. • 1 st difference is the same Quadratic • See same y more than once. • 2 nd difference is the same Exponential • y changes more quickly than x. • Never see the same y value twice. • Common multiplication pattern

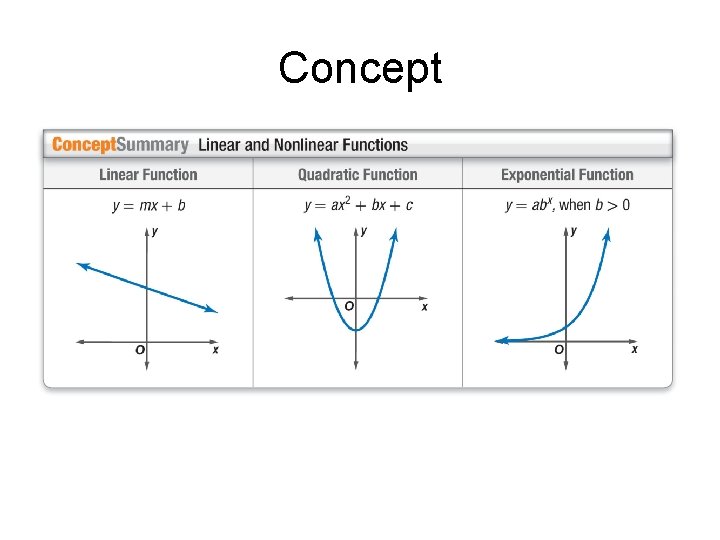
Concept

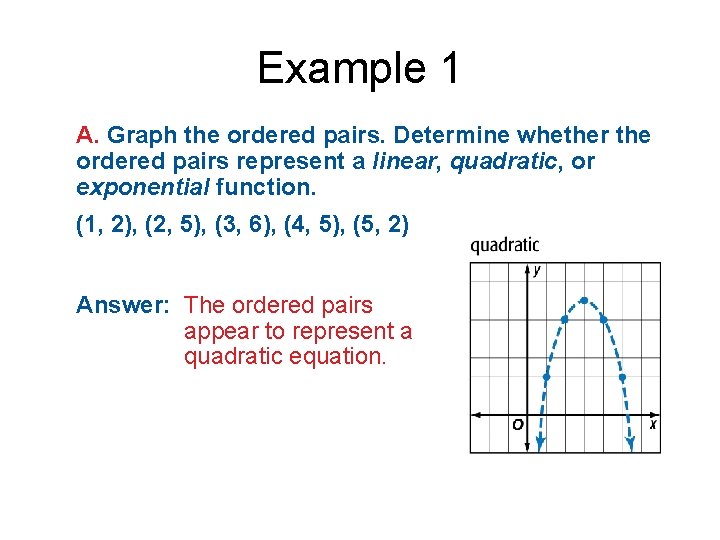
Example 1 A. Graph the ordered pairs. Determine whether the ordered pairs represent a linear, quadratic, or exponential function. (1, 2), (2, 5), (3, 6), (4, 5), (5, 2) Answer: The ordered pairs appear to represent a quadratic equation.

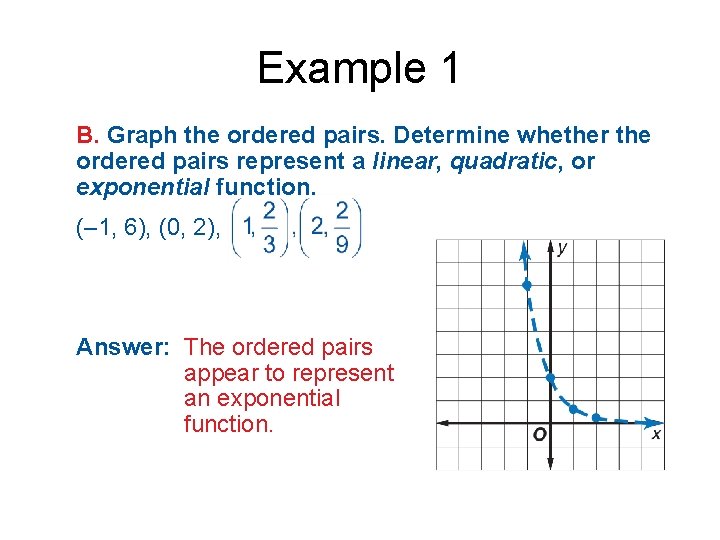
Example 1 B. Graph the ordered pairs. Determine whether the ordered pairs represent a linear, quadratic, or exponential function. (– 1, 6), (0, 2), Answer: The ordered pairs appear to represent an exponential function.

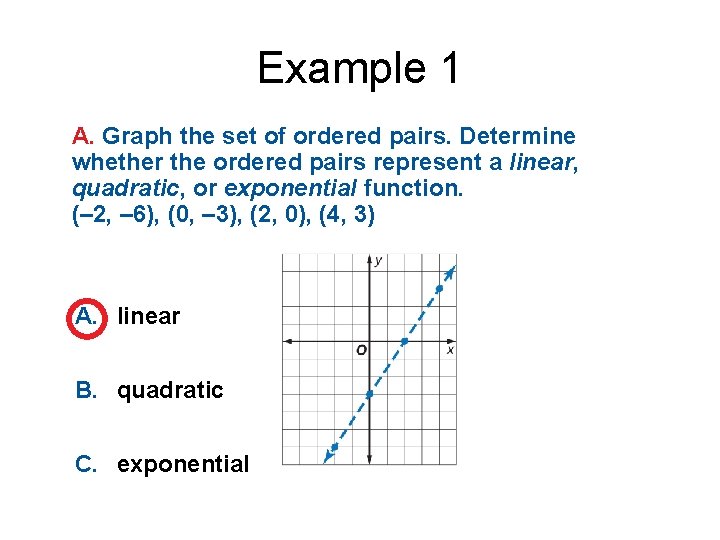
Example 1 A. Graph the set of ordered pairs. Determine whether the ordered pairs represent a linear, quadratic, or exponential function. (– 2, – 6), (0, – 3), (2, 0), (4, 3) A. linear B. quadratic C. exponential

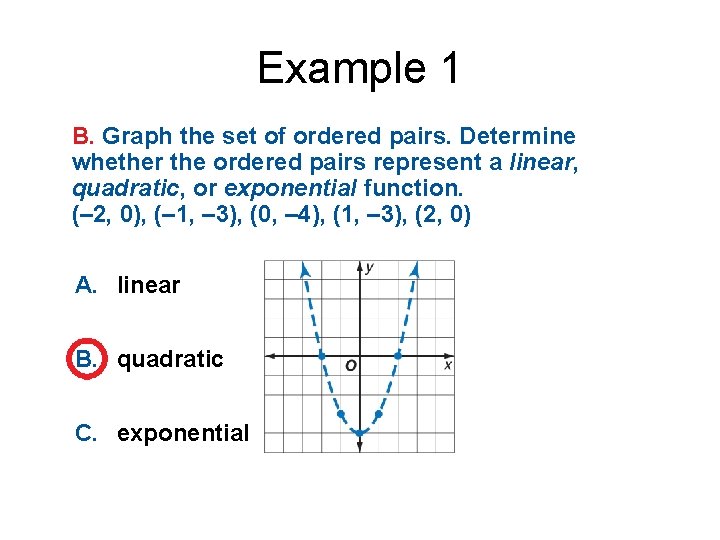
Example 1 B. Graph the set of ordered pairs. Determine whether the ordered pairs represent a linear, quadratic, or exponential function. (– 2, 0), (– 1, – 3), (0, – 4), (1, – 3), (2, 0) A. linear B. quadratic C. exponential

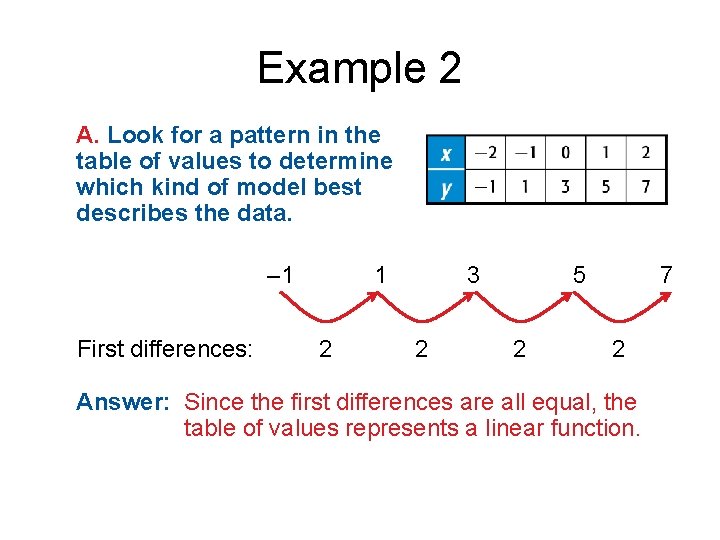
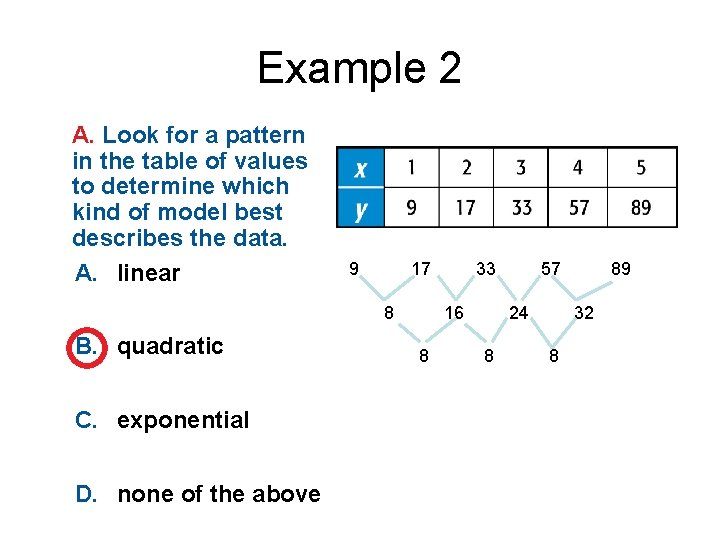
Example 2 A. Look for a pattern in the table of values to determine which kind of model best describes the data. – 1 First differences: 1 2 3 2 5 2 7 2 Answer: Since the first differences are all equal, the table of values represents a linear function.

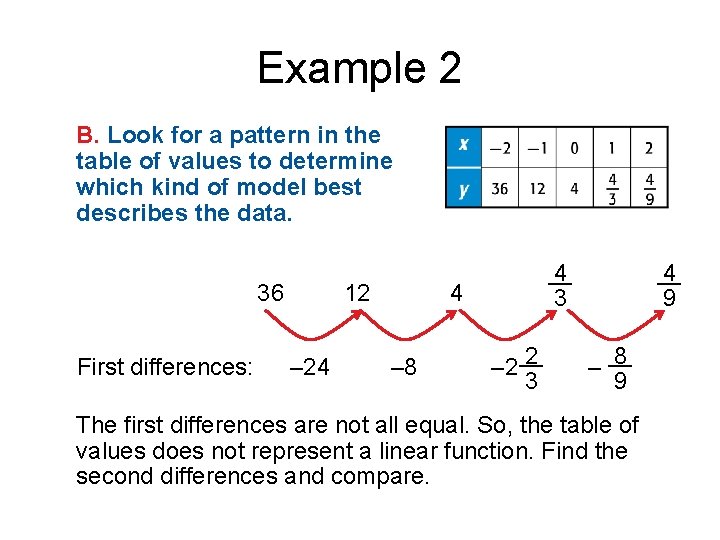
Example 2 B. Look for a pattern in the table of values to determine which kind of model best describes the data. 36 First differences: 12 – 24 __ 4 4 – 8 __ 4 3 2 – 2 __ 3 9 8 – __ 9 The first differences are not all equal. So, the table of values does not represent a linear function. Find the second differences and compare.

Example 2 – 24 First differences: – 8 1 5 __ 3 16 Second differences: 2 – 2 __ 3 8 – __ 9 7 1 __ 9 The second differences are not all equal. So, the table of values does not represent a quadratic function. Find the ratios of the y-values and compare. __ __ 4 4 36 12 4 3 9 Ratios: __ 1 3

Example 2 The ratios of successive y-values are equal. Answer: The table of values can be modeled by an exponential function.

Example 2 A. Look for a pattern in the table of values to determine which kind of model best describes the data. A. linear 9 17 8 B. quadratic C. exponential D. none of the above 33 16 8 57 24 8 89 32 8

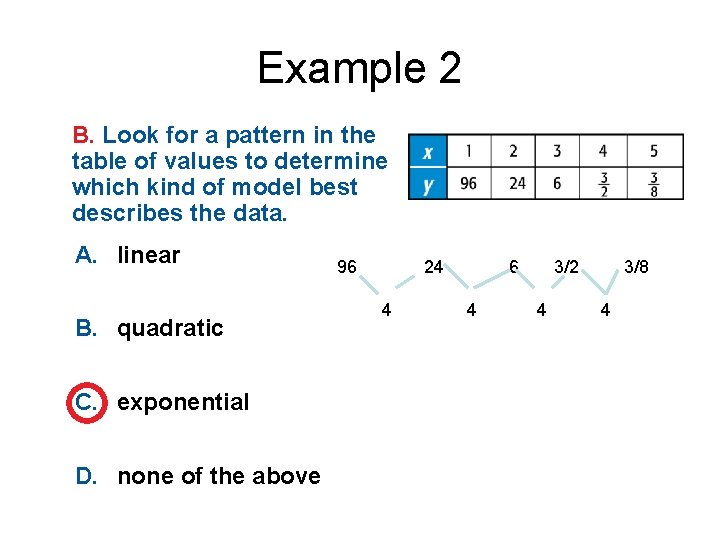
Example 2 B. Look for a pattern in the table of values to determine which kind of model best describes the data. A. linear B. quadratic C. exponential D. none of the above

Example 2 B. Look for a pattern in the table of values to determine which kind of model best describes the data. A. linear B. quadratic C. exponential D. none of the above 96 24 4 6 4 3/2 4 3/8 4

Write an Equation Example 3 Determine which kind of model best describes the data. Then write an equation for the function that models the data. Step 1 Determine which model fits the data. – 1 First differences: – 7 – 8 – 64 – 56 – 512 – 448 – 4096 – 3584

Write an Equation Example 3 First differences: – 7 Second differences: Ratios: – 1 – 56 – 49 – 8 × 8 – 448 – 3584 – 392 – 3136 – 64 – 512 × 8 – 4096 × 8 The table of values can be modeled by an exponential function.

Write an Equation Step 2 Example 3 Write an equation for the function that models the data. The equation has the form y = abx. Find the value of a by choosing one of the ordered pairs from the table of values. Let’s use (1, – 8). y = abx Equation for exponential function – 8 = a(8)1 x = 1, y = – 8, b = 8 – 8 = a(8) Simplify. – 1 = a An equation that models the data is y = –(8)x. Answer: y = –(8)x

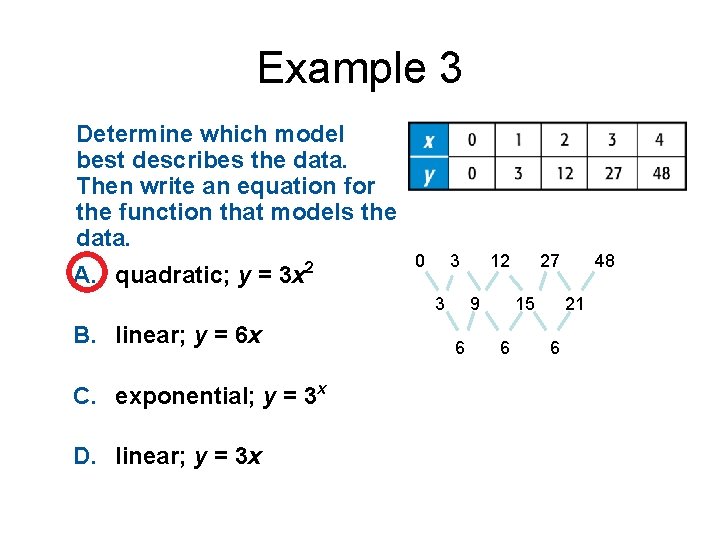
Example 3 Determine which model best describes the data. Then write an equation for the function that models the data. A. quadratic; y = 3 x 2 0 3 3 B. linear; y = 6 x C. exponential; y = 3 x D. linear; y = 3 x 12 9 6 27 15 6 48 21 6

Write an Equation for a Real-World Situation Example 4 KARATE The table shows the number of children enrolled in a beginner’s karate class for four consecutive years. Determine which model best represents the data. Then write a function that models that data.

Write an Equation for a Real. World Situation Example 4 Understand Plan Solve We need to find a model for the data, and then write a function. Find a pattern using successive differences or ratios. Then use the general form of the equation to write a function. The first differences are all 3. A linear function of the form y = mx + b models the data.

Write an Equation for a Real. World Situation Example 4 y = mx + b Equation for linear function 8 = 3(0) + b x = 0, y = 8, and m = 3 b =8 Simplify. Answer: The equation that models the data is y = 3 x + 8. Check You used (0, 8) to write the function. Verify that every other ordered pair satisfies the function.

Example 4 WILDLIFE The table shows the growth of prairie dogs in a colony over the years. Determine which model best represents the data. Then write a function that models the data. A. linear; y = 4 x + 4 B. quadratic; y = 8 x 2 C. exponential; y = 2 ● 4 x D. exponential; y = 4 ● 2 x

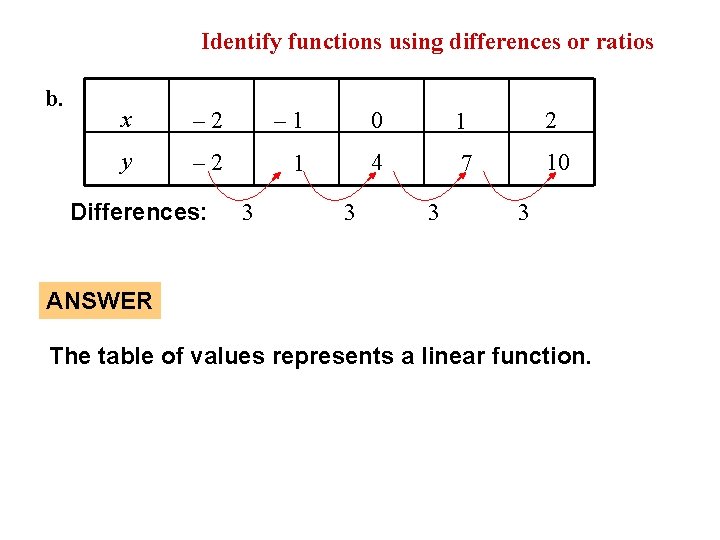
EXAMPLE 2 b. Identify functions using differences or ratios x – 2 – 1 0 1 2 y – 2 1 4 7 10 Differences: 3 3 ANSWER The table of values represents a linear function.

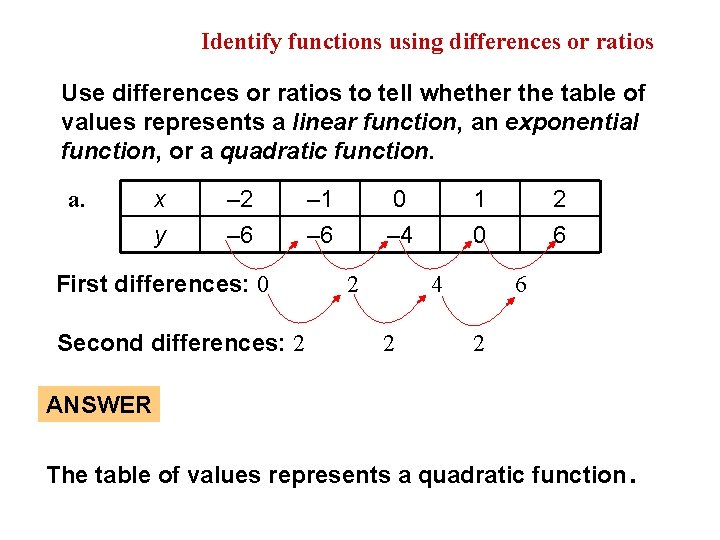
EXAMPLE 2 Identify functions using differences or ratios Use differences or ratios to tell whether the table of values represents a linear function, an exponential function, or a quadratic function. a. x y – 2 – 6 First differences: 0 Second differences: 2 – 1 – 6 0 – 4 2 1 0 4 2 2 6 6 2 ANSWER The table of values represents a quadratic function .

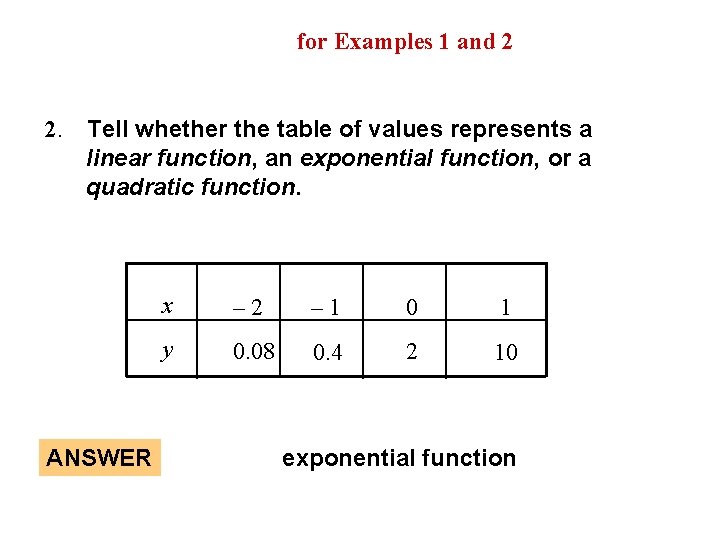
GUIDED PRACTICE for Examples 1 and 2 2. Tell whether the table of values represents a linear function, an exponential function, or a quadratic function. ANSWER x – 2 – 1 0 1 y 0. 08 0. 4 2 10 exponential function

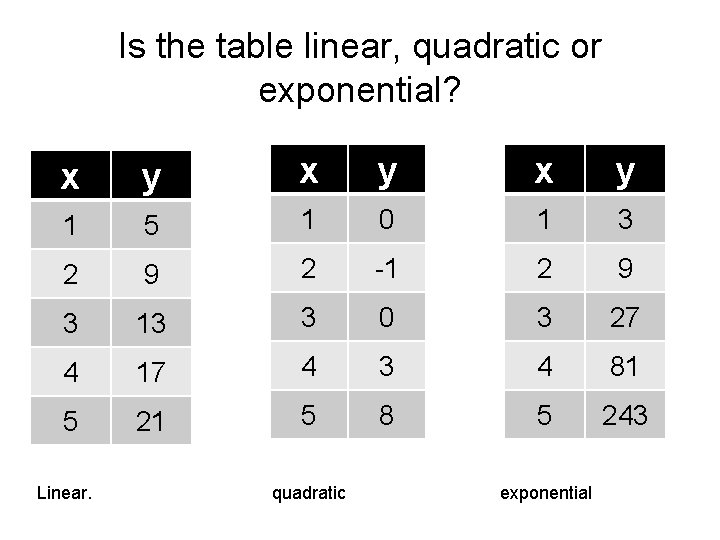
Is the table linear, quadratic or exponential? x y x y 1 5 1 0 1 3 2 9 2 -1 2 9 3 13 3 0 3 27 4 17 4 3 4 81 5 21 5 8 5 243 Linear. quadratic exponential