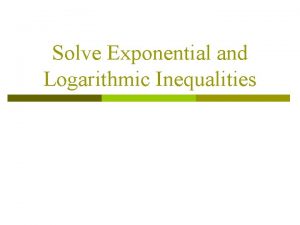Unit 3 Exponential and Logarithmic Functions Exponential Functions


































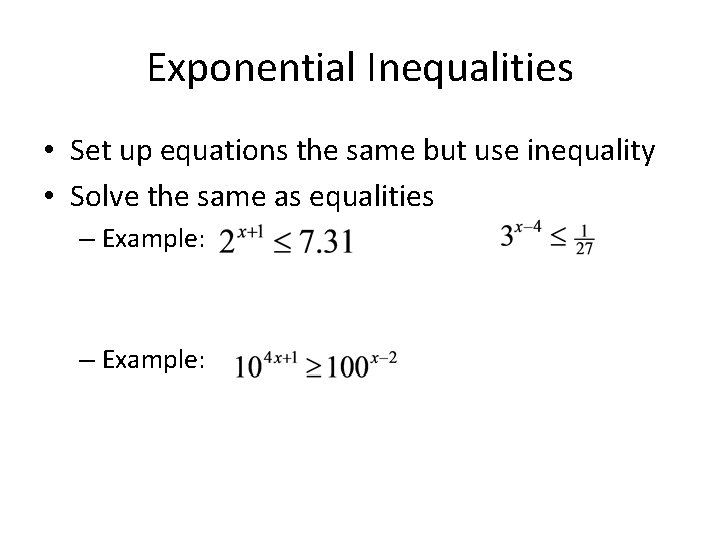


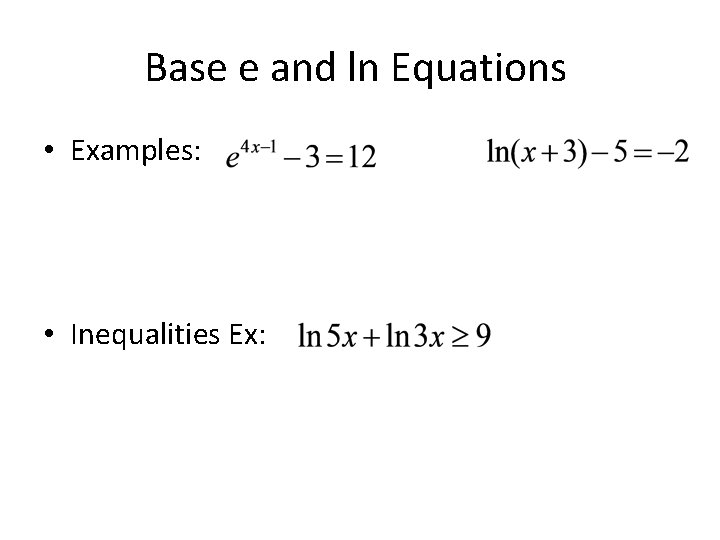

- Slides: 44

Unit 3 Exponential and Logarithmic Functions

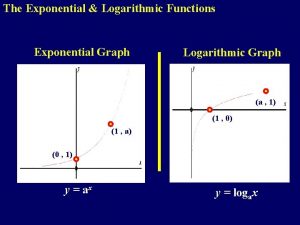
Exponential Functions – Alg 2: 4. 1 • Vocabulary – Exponential Function y=abx – Base (Common Ratio)- factor of change – Growth (Appreciation) – Decay (Depreciation) – Asymptote – line that a function approaches but never touches – Inverse Function (4. 2) – Logarithmic Function (4. 3 -4. 5) – Natural Log/Base e (4. 6)

Determine Growth vs Decay • Given y=abx • a= y-intercept (starting amount, initial amount) • b= growth or decay factor – If b > 1 = growth – If 0 < b < 1= decay

Graphing Exponential Functions • • Make a Table of Values Enter values of X and solve for Y Plot on Graph Examples: – Y = 2 x state D: – Y = (12)x state D: and R:

You can model growth or decay by a constant percent increase or decrease with the following formula: In the formula, the base of the exponential expression, 1 + r, is called the growth factor. Similarly, 1 – r is the decay factor.

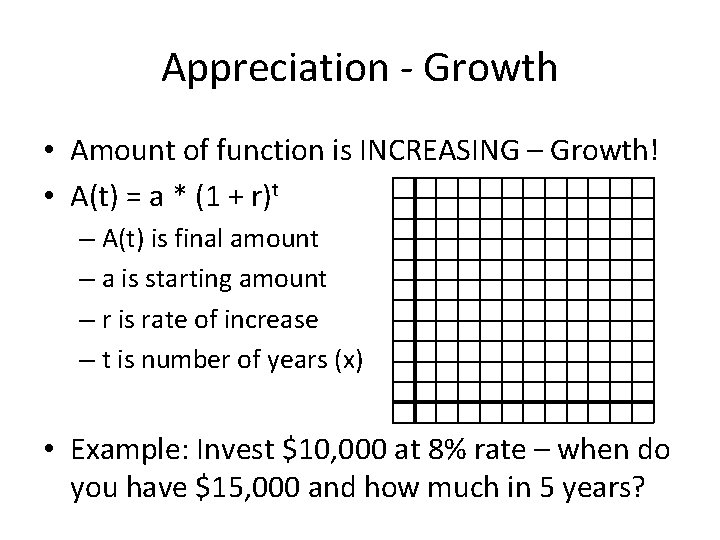
Appreciation - Growth • Amount of function is INCREASING – Growth! • A(t) = a * (1 + r)t – A(t) is final amount – a is starting amount – r is rate of increase – t is number of years (x) • Example: Invest $10, 000 at 8% rate – when do you have $15, 000 and how much in 5 years?

Depreciation - Decay • Amount of function is DECREASING – Decay! • A(t) = a * (1 - r)t – A(t) is final amount – a is starting amount – r is rate of decrease – t is number of years (x) • Example: Buy a $20, 000 car that depreciates at 12% rate – when is it worth $13, 000 and how much is it worth in 8 years?

Compounding Interest • Interest is compounded periodically – not just once a year • Formula is similar to appreciation/depreciation – Difference is in identifying the number of periods • A(t) = a ( 1 + r/n)nt – A(t), a and r are same as previous – n is the number of periods in the year

Examples of Compounding • You invest $750 at the 11% interest with different compounding periods for 1 yr, 10 yrs and 30 yrs: – 11% compounded annually – 11% compounded quarterly – 11% compounded monthly – 11% compounded daily

Continuous Compounding • Continuous compounding is done using e – e is called the natural base – Discovering e – compounding interest lab • Equation for continuous compounding – A(t) = a*ert • A(t), a, r and t represent the same values as previous • Example: $750 at 11% compounded continuously

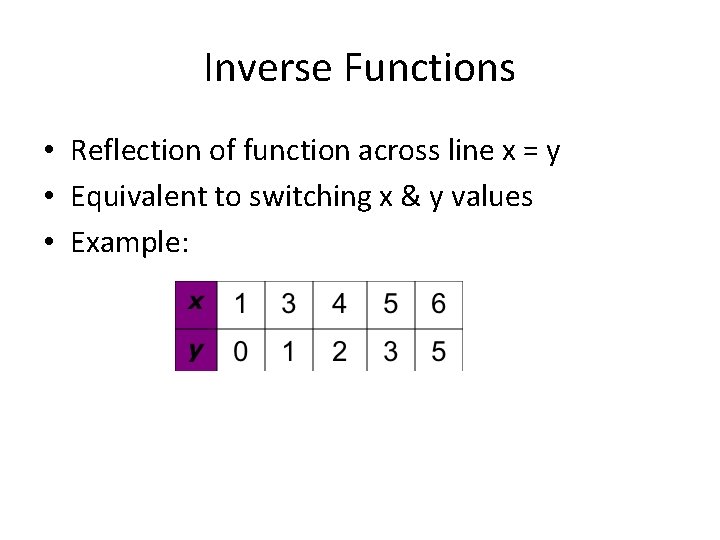
Inverse Functions • Reflection of function across line x = y • Equivalent to switching x & y values • Example:

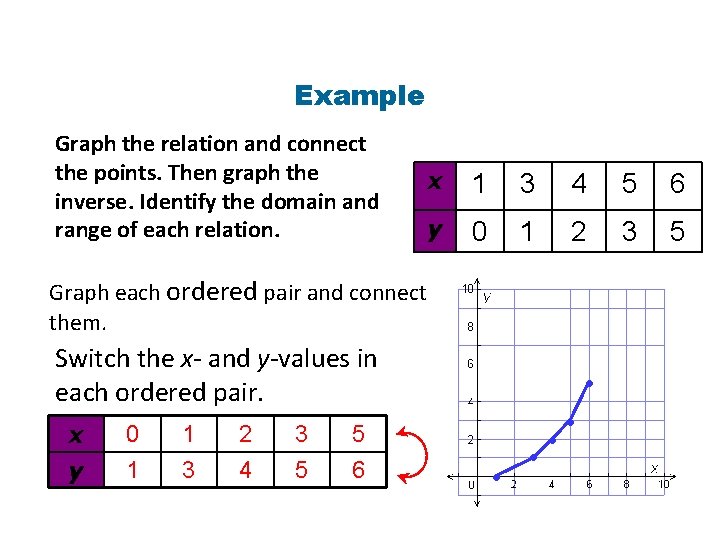
Example Graph the relation and connect the points. Then graph the inverse. Identify the domain and range of each relation. x 1 3 4 5 6 y 0 1 2 3 5 Graph each ordered pair and connect them. Switch the x- and y-values in each ordered pair. x y 0 1 1 3 2 4 3 5 5 6 • • •

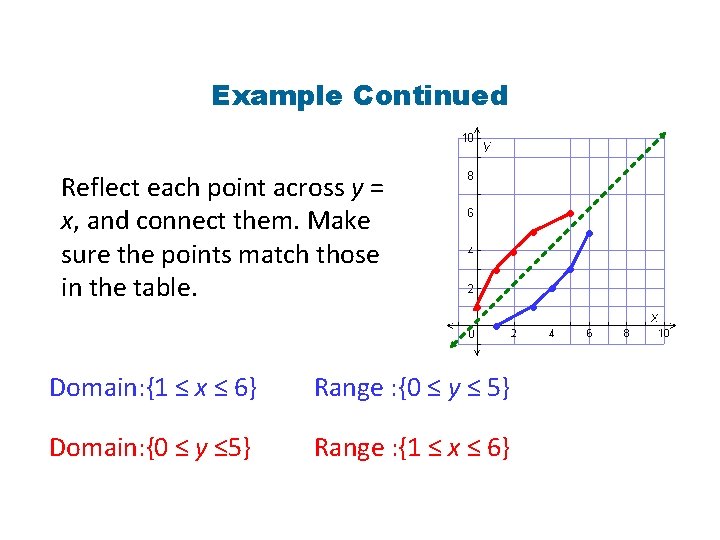
Example Continued Reflect each point across y = x, and connect them. Make sure the points match those in the table. • • Domain: {1 ≤ x ≤ 6} Range : {0 ≤ y ≤ 5} Domain: {0 ≤ y ≤ 5} Range : {1 ≤ x ≤ 6} • • •

Inverse Functions • Steps for creating an inverse 1. 2. 3. 4. Rewrite the equation from f(x) = to y = Switch variables (letters) x and y Solve equation for y (isolate y again) Rewrite new function as f-1(x) for new y

Inverse Functions • Once inverse is set up, use opposite operations – If adding – subtract – If subtracting – add – If multiplying – divide – If dividing – multiply

Undo operations in the opposite order of the order of operations. Helpful Hint The reverse order of operations: Addition or Subtraction Multiplication or Division Exponents Parentheses

Inverse Functions - Examples • Example: f(x) = 2 x – 3 • Example: f(x)=

Example: Retailing Applications Juan buys a CD online for 20% off the list price. He has to pay $2. 50 for shipping. The total charge is $13. 70. What is the list price of the CD? Step 1 Write an equation for the total charge as a function of the list price. c = 0. 80 L + 2. 50 Charge c is a function of list price L.

Example Continued Step 2 Find the inverse function that models list price as a function of the change. c – 2. 50 = 0. 80 L Subtract 2. 50 from both sides. c – 2. 50 = L 0. 80 Divide to isolate L. Beware: Don’t change variables (letters) in word problems – they mean or represent something

Example Continued Step 3 Evaluate the inverse function for c = $13. 70. Substitute 13. 70 – 2. 50 L= for c. 0. 80 = 14 The list price of the CD is $14. Check c = 0. 80 L + 2. 50 = 0. 80(14) + 2. 50 = 11. 20 + 2. 50 = 13. 70 Substitute.

Logarithms – Alg. 2: Chap 4. 3 • Inverse of an exponential function • Logbx = y – b is the base (same as exponential function) – Converts to: by = x • From exponential function: bx = y • Write logarithmic function: logby = x • If there is no base indicated – it is base 10 • Example: log x = y

You can write an exponential equation as a logarithmic equation and vice versa. Reading Math Read logb a= x, as “the log base b of a is x. ” Notice that the log is the exponent.

Example 1: Converting from Exponential to Logarithmic Form Write each exponential equation in logarithmic form. Exponential Equation Logarithmic Form 35 = 243 log 3243 = 5 1 2 The base of the exponent becomes the base of the logarithm. 1 2 25 = 5 log 255 = 104 = 10, 000 log 1010, 000 = 4 6– 1 = ab = c 1 6 log 6 1 = – 1 6 logac =b The exponent is the logarithm. An exponent (or log) can be negative. The log (and the exponent) can be a variable.

Example 2: Converting from Logarithmic to Exponential Form Write each logarithmic form in exponential equation. Logarithmic Form Exponential Equation 1 log 99 = 1 9 =9 log 2512 = 9 29 = 512 log 82 = log 4 1 16 1 3 = – 2 logb 1 = 0 The base of the logarithm becomes the base of the power. The logarithm is the exponent. 1 3 8 =2 4– 2 = b 0 = 1 1 16 A logarithm can be a negative number. Any nonzero base to the zero power is 1.

Solving & Graphing Logarithms • • Write out in exponential form: b? = x What value needs to go in for ? Example: log 327 = ? Graphing – – Plot out the Exponential Function – Table of values – Switch the x and y coordinates – Domain of exponential is range of logarithm (limits) – Range of exponential is domain of logarithm (limits) • Example: Plot 2 x and then log 2 x

Properties of Logarithms Alg 2: 4. 4 • Product Property: logbx + logby = logb(x*y) – Example: log 64 + log 69 • Quotient Property: logbx – logby = logb(x/y) – Example: log 5100 – log 54 • Power Property: logbxy = y*logbx – Examples: log 104 log 5252

Example 1: Product Property Express log 64 + log 69 as a single logarithm. Simplify. log 64 + log 69 log 6 (4 9) To add the logarithms, multiply the numbers. log 6 36 Simplify. 2 Think: 6? = 36.

Example 2: Quotient Property Express log 5100 – log 54 as a single logarithm. Simplify, if possible. log 5100 – log 5 4 log 5(100 ÷ 4) To subtract the logarithms, divide the numbers. log 525 Simplify. 2 Think: 5? = 25.

Example 3 – Power Property Express as a product. Simplify, if possibly. a. log 104 b. log 5252 4 log 10 4(1) = 4 2 log 525 Because 101 = 10, log 10 = 1. 2(2) = 4 Because 52 = 25, log 525 = 2.

More Logarithmic Properties • Inverse Property: logbbx = x & blogbx = x – Example: log 775 – Example: 10 log 2 • • Change of Base: logbx = Example: log 48 Example: log 550 Change of base in Calculator: MATH, log. BASE( – log--- : type base in first then value

Example: Geology Application The tsunami that devastated parts of Asia in December 2004 was spawned by an earthquake with magnitude 9. 3 How many times as much energy did this earthquake release compared to the 6. 9 -magnitude earthquake that struck San Francisco in 1989? The Richter magnitude of an earthquake, M, is related to the energy released in ergs E given by the formula. Substitute 9. 3 for M.

Example Continued Multiply both sides by 23. æ E ö 13. 95 = log ç 11. 8 ÷ è 10 ø Simplify. Apply the Quotient Property of Logarithms. Apply the Inverse Properties of Logarithms and Exponents.

Example Continued Given the definition of a logarithm, the logarithm is the exponent. Use a calculator to evaluate. The magnitude of the tsunami was 5. 6 1025 ergs.

Example Continued Substitute 6. 9 for M. Multiply both sides by 23. Simplify. Apply the Quotient Property of Logarithms.

Example Continued Apply the Inverse Properties of Logarithms and Exponents. Given the definition of a logarithm, the logarithm is the exponent. Use a calculator to evaluate. The magnitude of the San Francisco earthquake was 1. 4 1022 ergs. 25 5. 6 10 The tsunami released = 4000 times as much energy as 22 1. 4 10 the earthquake in San Francisco.

Solving Exponentials and Logarithms Alg 2: 4. 5 • If the bases of two equal exponential functions are equal – the exponents are equal – If bases don’t look equal – try and make them (Ex 3) – Examples: 3 x = 32 7 x+2 = 72 x 48 x = 16 – Examples: • Logarithms are the same: common logarithms with common bases are equal – Examples: log 7(x+1) = log 75 – Examples: log 3(2 x+2) = log 33 x

Solving Exponentials - continued • Exponents without common bases – Get exponential by itself – Convert to logarithm • Examples: – 5 x = 7 3(2 x+1) = 15 6(x+1) + 3 = 12

Solving Logarithms – continued • Logarithms with logs only on one side – Use the properties of logarithms to solve – Get one log by itself – Must convert to exponential • Examples: (Using properties of logarithms) – Log 3(x – 5) = 2 – Log 2 x 2 = 8 log 45 x – log 3 = 1 log x + log (x+9) = 1
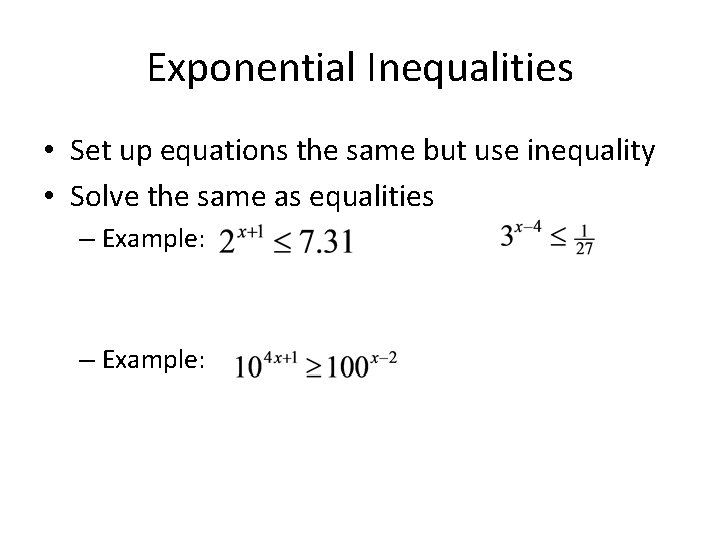
Exponential Inequalities • Set up equations the same but use inequality • Solve the same as equalities – Example:

Log Inequalities • Remember Domain of Log is • Only positive x values Examples:

Natural Logarithm • Inverse of natural base, e • Written as ln – Shorthand way to write loge – Properties are the same as for any other log • Examples: Inverse operations – ln e 3. 2 eln(x-5) e 2 ln x • Convert between e and ln – ex = 5 ln x = 43 ln e 2 x+ln ex
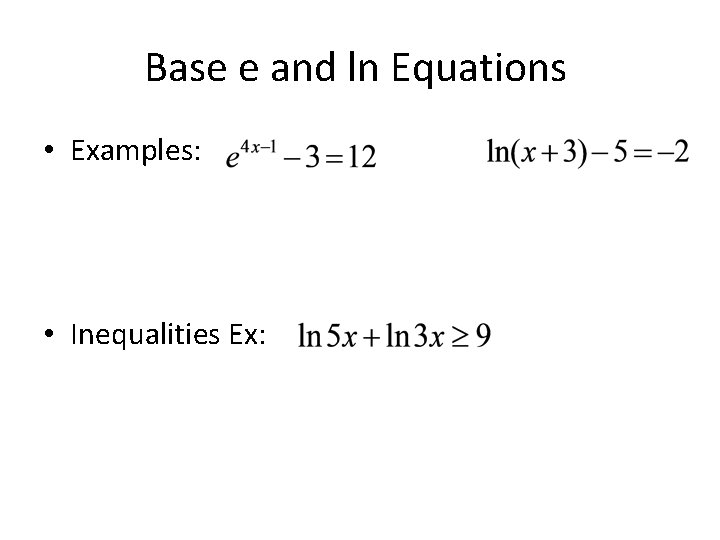
Base e and ln Equations • Examples: • Inequalities Ex:

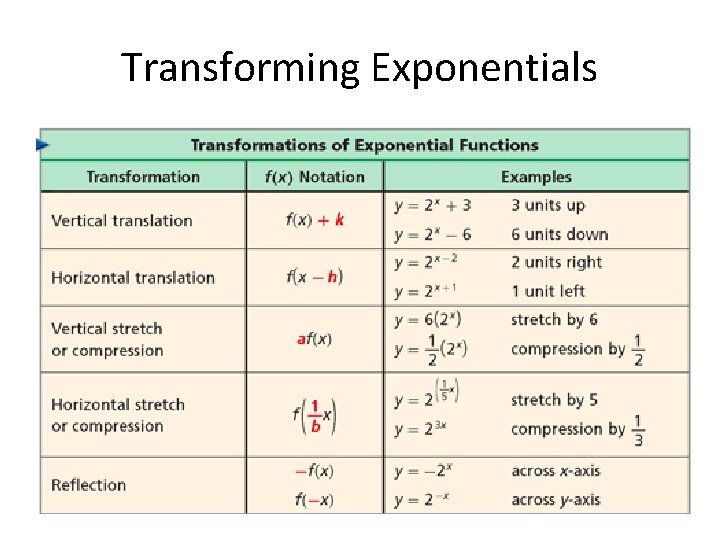
Transforming Exponentials

Transforming Logarithms
 Unit 8 exponential and logarithmic functions
Unit 8 exponential and logarithmic functions Examples of exponential equations
Examples of exponential equations Exponential table of values
Exponential table of values Chapter 6 exponential and logarithmic functions answers
Chapter 6 exponential and logarithmic functions answers Chapter 4 exponential and logarithmic functions
Chapter 4 exponential and logarithmic functions Chapter 4: exponential and logarithmic functions answer key
Chapter 4: exponential and logarithmic functions answer key Chapter 10 exponential and logarithmic functions answers
Chapter 10 exponential and logarithmic functions answers Chapter 10 exponential and logarithmic functions answers
Chapter 10 exponential and logarithmic functions answers Transforming exponential and logarithmic functions
Transforming exponential and logarithmic functions The inverse of exponential function is a composite function
The inverse of exponential function is a composite function Chapter 5 exponential and logarithmic functions
Chapter 5 exponential and logarithmic functions Condensing logarithmic functions
Condensing logarithmic functions Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 9 exponential and logarithmic functions answer key
Chapter 9 exponential and logarithmic functions answer key Chapter 5 exponential and logarithmic functions answer key
Chapter 5 exponential and logarithmic functions answer key Transcendental functions examples with solutions
Transcendental functions examples with solutions Solving exponential and logarithmic functions calculator
Solving exponential and logarithmic functions calculator Inverse functions
Inverse functions Logarithmic exponential and other transcendental functions
Logarithmic exponential and other transcendental functions Chapter 5 exponential and logarithmic functions
Chapter 5 exponential and logarithmic functions Chapter 3 exponential and logarithmic functions
Chapter 3 exponential and logarithmic functions 7-5 exponential and logarithmic equations and inequalities
7-5 exponential and logarithmic equations and inequalities 7-5 exponential and logarithmic equations
7-5 exponential and logarithmic equations Logarithmic inequalities example
Logarithmic inequalities example Logarithmic equations and inequalities
Logarithmic equations and inequalities Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Log to exponential form
Log to exponential form Quiz 7-2 logarithmic expressions and functions
Quiz 7-2 logarithmic expressions and functions 3-4 exponential and logarithmic equations
3-4 exponential and logarithmic equations 3-4 exponential and logarithmic equations
3-4 exponential and logarithmic equations Exponentiating both sides
Exponentiating both sides Curve fitting with exponential and logarithmic models
Curve fitting with exponential and logarithmic models 3-4 exponential and logarithmic equations
3-4 exponential and logarithmic equations Logarithmic inequality example
Logarithmic inequality example Logarithmic decline
Logarithmic decline Graphing exponential inequalities
Graphing exponential inequalities How to write logarithmic form
How to write logarithmic form Logarithmic to exponential form
Logarithmic to exponential form Exponential微分
Exponential微分 Linear quadratic exponential examples
Linear quadratic exponential examples Log exponential form
Log exponential form Vertical stretch
Vertical stretch Log m.n
Log m.n Exponential rule integral
Exponential rule integral 4-3 logarithmic functions answers
4-3 logarithmic functions answers